どうも、こんにちはDKです。
ここでは、中学生で習う数学の基礎を解説しているよ。
今回は中学2年生で習う、確率についてやっていきますね。
確率っていうのは、数学としては、高校受験で1問は出題されるところになるし
大人になっても、確率に関わることっていうのは少なくないので
ここで、しっかり学んでいってもらいたいと思います。
ちなみに、「確率」の定義はって言うと
あることがらが起こることが期待される程度を表す数
ってことになって、その数を0以上、1以下で対応させたものになるんだね。
動画でも基礎の解説を行なっているので、そちらも見てみて下さい
(動画は音が出るので注意して)
では、基礎の解説やっていきますね。
(1)確率の求め方
まずは確率の求め方について確認してみよう。
一般的なサイコロがあって、このサイコロを投げた時に出た目っていうのは
1から6のどれかってことになるよね。
このサイコロを数回、投げた時に1から6の出た目の数を数えていくと。。
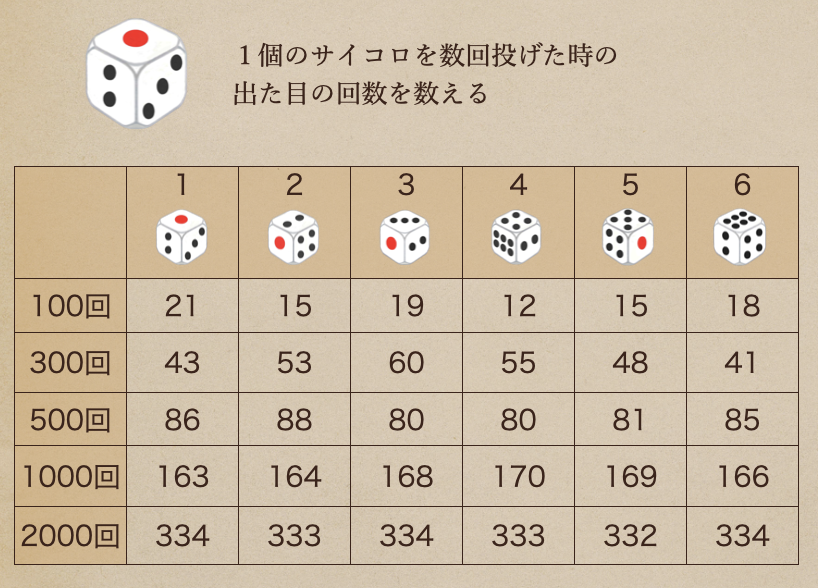
サイコロを投げる回数が多いほど、どの目が出る回数もほぼ等しくなっているんだね。
こんな風に、サイコロっていうのは1〜6のどの目が出ることも同じくらい
期待ができるってことが言えるんだね。これっていうのがサイコロの1から6のどの目が出ることも
同様に確からしいっていう言い方をするんだね。
「同様に確からしい」っていうのはサイコロを6回投げたら同じ目が出たりするんだろうけど
それをそれぞれの目が1回ずつ出ますよってことを決め事にしているってことなんだね。
「同様に確からしい」時っていうのは次のように確率っていうのを求めることができるんだね。
【確率の求め方】
あることがらが起こり得る場合が全部で n 通りあって
どれが起こることも「同様に確からしい」とき
その中から、ことがら A の起こる場合が a 通りある時
A の起こる確率 \(p\) は \(p=\frac{a}{n}\) となる
例えば
(1) サイコロを1回投げて、1の出る確率 \(p1\) は・・・ \(p1=\frac{1}{6}\)
(2) サイコロを1回投げて、偶数の出る確率 \(p2\) は・・・ \(p2=\frac{3}{6}=\frac{1}{2})\)
となるんだね。
サイコロは1から6までなので起こり得る全てのことがらは 6通り で
(1)の1の出ることがらは 1通り
(2)の偶数の出ることかがらは、2,4,6 の 3通り
ってことになるんだね。
これが確率ってことで、定義にもある「期待される程度を数で表す」で
(1)の1の目が出る確率は6回に1回は1が出ることが期待されるってことで
(2)の偶数の出る確率は2回に1回は偶数が出ることが期待されるってことに
なるんだね。
確率っていうのは、期待される程度を数で表しているってことなので
回数が少ないと確率通りにはならないこともあるってことは覚えておいてね。
(2)確率と場合の数
次の硬貨の裏表で確率を考えてみるね。

硬貨の裏表っていうのは、2通りになるよね。
今回のように、複数のことがらにおける組み合わせによって全てのことがらを確認する場合
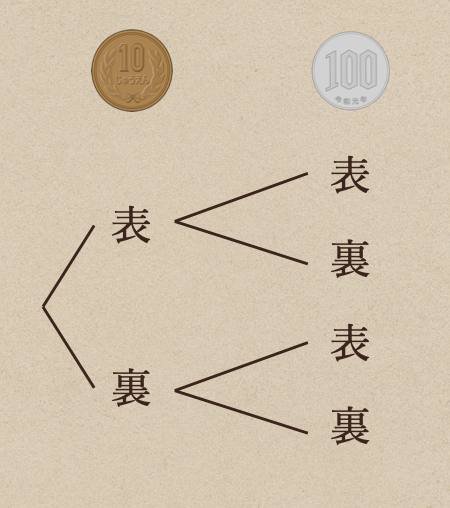
こんな風に、10円玉のことがらを書き出し、その後、100円玉のことがらを
書き出してあげることで、すべてのことがらっていうのを表してあげているんだね。
これで、すべてのことがらは4通りで、2枚ともが表になるのは1通りってことが
わかって、2枚とも表となる確率 \(p\) は \(p=\frac{1}{4}\) ってことになるんだね。
このように、すべてのことがらを図にして書き出すことを
「樹形図(じゅけいず)」って言うんだね。
そして、あることがらが考えられる数(OO通り)のことを
場合の数(ばあいのかず)っていう言い方をするんだね。
なので、さっき「2枚の硬貨の表、裏のすべての場合の数は」っていうと
4通りってことになって、「2枚ともが表である場合の数は」っていうと
2通りってことになるんだね。
次に、もう一つ確率について考えてみよう。

この場合もサイコロ2個の出た目の組み合わせって言うのを見てみないと
全部で何通りあるのかっていうのがわからないですよね?
かといって、これを樹形図で書いていくと
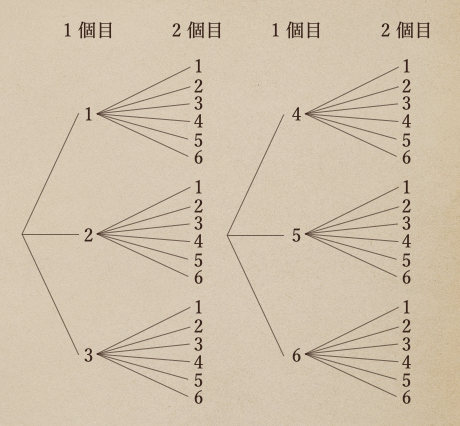
組み合わせが多くて、樹形図が大きくなってしまって
書ききれなくなったりしちゃうよね。
こんな時は、表を使って書くことも有効で
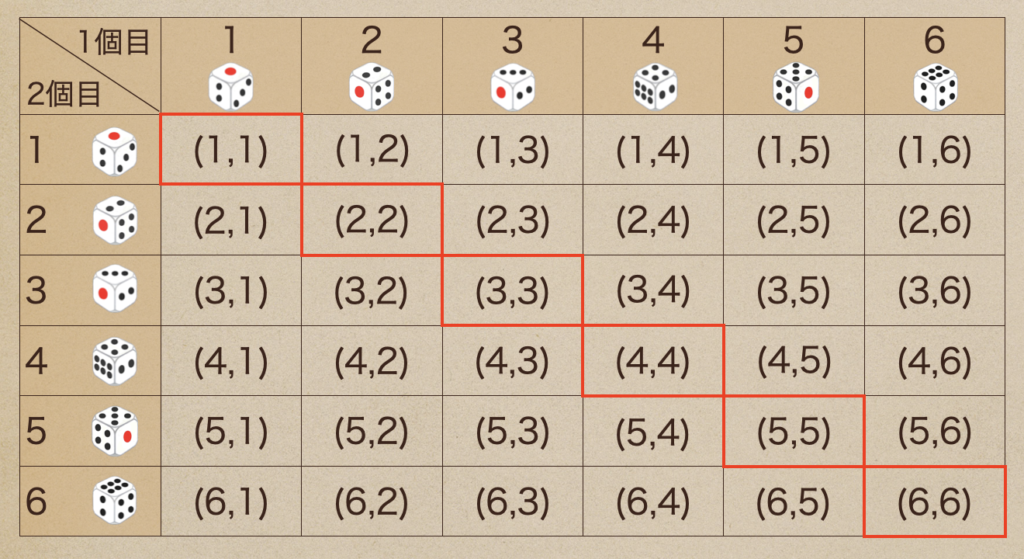
これで、全部で36通りの場合があるってことがわかって
同じ目が出るのは赤枠で囲った6通りになるってことだね。
なので、同じ目が出る確率 \(p\) は・・・\(p=\frac{6}{36}=\frac{1}{6}\)
が求められたね。
確率で、すべてのことがらが何通りあるのかわからないってなった場合は
この樹形図や表を使って、見てあげるようにしよう。
そうすることで、もれや重なりっていうのをなくすことができるんだね。
確率の何通りあるのかを考えるときに、和の法則、積の法則っていうのがあるので
それも、ここで確認しておくね。
【和の法則】
起こり得ることがらAとBが同時に起こらないとき
Aを \(m\) 通り、Bを \(n\) 通りとしたとき
AまたはBの起こる場合の数は \(m+n\) 通り となる
この和の法則の例をあげると
サイコロを振った時の目が2以下または5以上であるときの場合の数は?
この場合、2以下は [ 1 , 2 ] の2通り、5以上は [ 5 , 6 ] の2通りとなり
2以下と5以上は同時には起こり得ないのでこの時の場合の数は
2通り + 2通り = 4 通り となる
こんな風に、ことがらが同時には起こらない場合の数を求めるときは
足す(和)で求めてあげればいいってことになるんだね。
【積の法則】
起こり得ることがらAとBが同時に起こるとき
Aを \(m\) 通り、Bを \(n\) 通りとしたとき
AまたはBの起こる場合の数は \(m×n\) 通り となる
例としては
2個のサイコロを投げたとき、起こり得る全ての場合の数は?
サイコロ1個の起こり得る場合の数は 6 通り
サイコロ2個の全ての場合の数 \(6×6=36\) 通り となる
2つ以上のことがらが同時に起こった場合は、それぞれのことがらの
起こる場合の数の積ですべてのことがらの場合の数を求めることができるってことだね。
この場合の数っていうのは、同時に起こるものなのか、同時には起こらないものなのかに
よって、計算の仕方っていうのは変わってくるので、2つ以上のことがらの確率を
考える時にはそれぞれのことがらの関係を考えてあげるようにしていきましょう。
確率っていうのは、分数で表されるよね?
例えば、サイコロを1回振って1の目が出る確率は?っていうと \(\frac{1}{6}\) だよね。
じゃあ、サイコロを1回振って、1の目、2の目・・・6の目が出る確率っていうと
それぞれ、\(\frac{1}{6}\) ってことになるよね。
これらの確率をすべて足すと\(\frac{1}{6}+\frac{1}{6}+\frac{1}{6}+\frac{1}{6}+\frac{1}{6}+\frac{1}{6}=\frac{6}{6}=1\) と
なるよね。これっていうのは、サイコロを1回振って、1から6の目が出る確率のことを
言っているんだね。
ようするに確率の範囲っていうのは \(0≦p≦1\) (\(p\)は確率)ってことになるんだね。
これはすべての起こり得る確率はっていうと「1」になるってことで
これから、サイコロを1回振って、1以外の目が出る確率は?ってことを
求めたいとき、1以外の目となるので、起こり得る場合の数は5なので
確率は\(\frac{5}{6}\) として求めることができるんだけど
これっていうのはすべての起こり得る確率「1」から1の目の確率\(\frac{1}{6}\)を
引いてあげることでも、求めることができるんだね。\(1-\frac{1}{6}\=\frac{5}{6}\)
これを利用して次のような場合の確率を求めていくこともできるんだね。
【あることがらが起こらない確率】
(Aの起こらない確率)=1-(Aの起こる確率)
今回の例をサイコロで説明したので、1の目以外の起こる確率っていうのは
簡単に求めることができたんだけど、あることがらが起こらない場合の数を
求めるってなると大変な場合も多いので、簡単に求めて行ける方法を選んで
確率を求めるようにしていこう。
今回は、ここまでになります。
ここまでの記事が良かったと思ったらここをクリックしてね。
質問なんかがあった場合はコメントにお願いします。
では、またさようなら



コメント