どうも、こんにちはDKです。
今回は正の数、負の数の計算の続き、乗法と除法をやっていくよ。
この内容は動画でも見れるよ。動画とブログの両方を見ながらわからないことろを
繰り返し、見てみてね。※音が出るから試聴するときは注意してね。
正の数、負の数の乗法
それぞれ、正の数、負の数の乗法の組み合わせで、積(答え)がどうなるか考えてみよう。
①正の数×正の数
2×3=6だよね。これに符号をつけて考えると(+2)×(+3)=(+6) だね。
ようするに、正の数×正の数=正の数 てことだね。
次に負の数×正の数を考えてみよう。
②負の数×正の数
(ー2)×(+3)の場合とかだね。これって、(ー2)を3回足すってことだよね?
ようするに(ー2)×(+3)=(ー2)+(ー2)+(ー2)=(ー6)てなるね。
(ー2)×(+3)=(ー6) 負の数×正の数=負の数になるってことがわかったね。
じゃあ、次に正の数×負の数を考えてみようか。
③正の数×負の数
(+2)×(ー3)だね。(+2)を(ー3)回足す??よくわからないね。
この場合、こうやって考えてみようか。
(+2)×(+3)から順に、かける数字を小さくしていった時に積(答え)はどうなるかな?

(+2)×(ー3)=ー6ってことがわかったよね。他にも同じようになるか試してみてね。
このことから、正の数×負の数=負の数ってことがわかったね。
今度は負の数×負の数をやってみよう。
④負の数×負の数
(ー2)×(ー3)は(ー2)をー3回かけることだけど、これもよくわからないよね。
さっきと同様に(ー2)×(+3)から1つずつ小さくしてみて考えてみよう。

(ー2)×(ー3)=+6ってことがわかったね。
これって負の数にかける数が小さくなると、積は大きくなることがわかったね
正の数、負の数の乗法の組み合わせによってこんなことがわかったね。
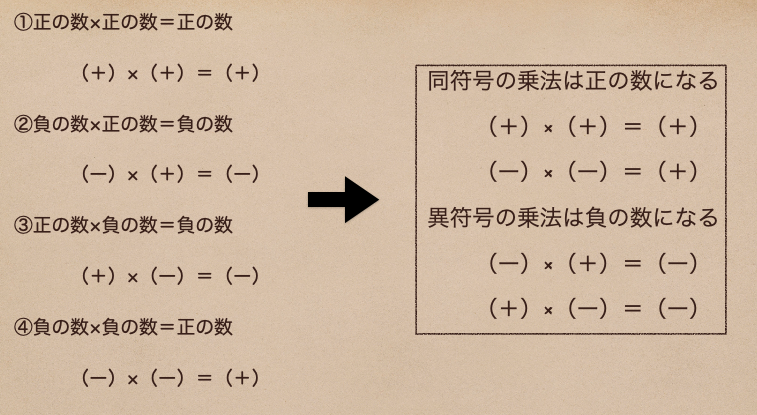
これが、正の数、負の数の乗法の基本となるから、しっかり覚えておこう。
また、乗法には加法と同じ法則があるんだ、一緒に覚えておこう。
乗法の交換法則・・a × b = b × a
例:4×6=6×4、(ー4)×6=6×(ー4)
加法の結合法則・・( a × b ) × c = a × ( b × c )
例:(4×6)×5=4×(6×5)
これも、加法の法則と同じで、乗法の場合はどこから計算してもオッケーってことだね。
次に除法(割り算)について学んでいこう。
正の数・負の数の除法
除法は割り算のことだよね。ってことは例えば、6÷2 っていうのは□×2=6で□を
求めれば、6÷2の商が求められることになるよね。
この場合、 3×2=6だから□=3だよね。6÷2=3ってなるよね。
同様に、次の乗法から除法を考えてみよう。
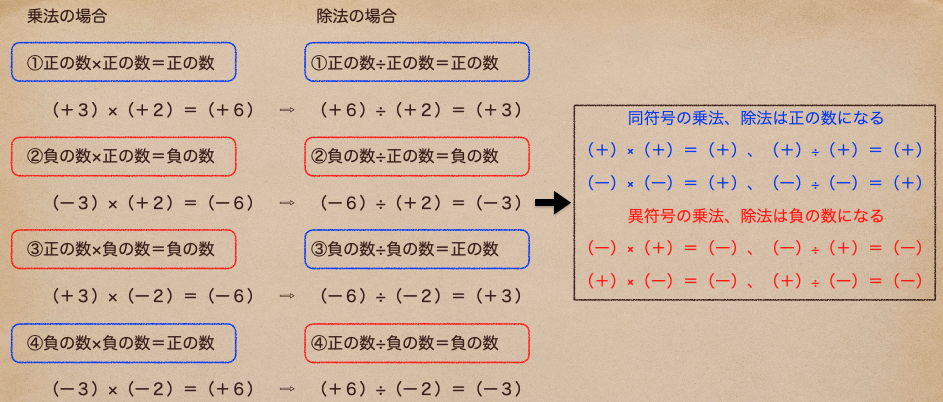
乗法、除法とも、同符号の場合は正の数になって、異符号の場合は負の数になることがわかったね。
小数や分数を含む、乗法、除法も同じ計算方法になるからね。
分数の場合、逆数というものがあってこれは
2つの数の積が1になるとき、一方の数を他方の数の逆数っていうんだね。

除法には次のことができるからここはしっかり押さえておこうね。
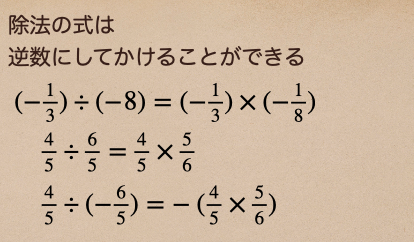
これをすることによって、除法の式を乗法の式にすることができるんだ。
そうすると、乗法の交換法則や結合法則が使えて、式を簡単にすることができるよ。
じゃあ、次は乗法、除法の混じった計算を考えてみよう。
乗法と除法の混合計算
乗法と除法を計算する上で、次のことを覚えておこうね。

これは、乗法、除法だけの式の場合、すべてに当てはまることなんだ。
だから、正・負の符号の数で答えの符号が決まってくるんだね。
じゃあ、3つ以上の数の乗法を計算してみるね。
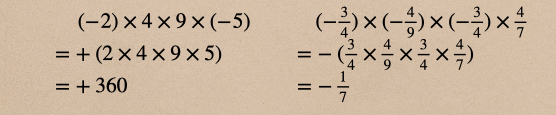
左側は整数4つの数の乗法だね、負の符号の数は2つだよね?だからこの積は”+”になるんだね。
右側は分数4つの数の乗法だよ。負の符号の数は3つあるね?この時の積は”ー”になるんだよ。
こんな風に乗数の数が増えても、負の符号の数を先に見ておくことで
その積が”+”になるか、”ー”になるかわかるよね。
じゃあ、次に乗法、除法が混ざった式をみていこう。

乗法、除法が混ざった式は
①式を”×”にする・・・上の式では”÷(ー6)”を逆数にして”×(ー6)”にしているね。
②符号を合わせる・・・上の式では負の符号が3つ(奇数)あるから答えは”ー”になるよね。
③計算する・・・”()”の中を計算するだけだよ。
乗法と除法の混ざった式を計算するときは注意することがあるんだ。
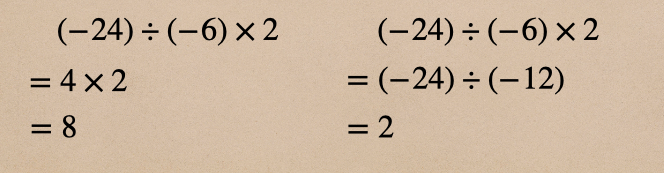
次の式で別々の計算をしているんだけどちがいはわかるかな?
左の式も右の式も同じだけど、答えが違うね!?
なぜかわかる?左の式は(ー24)÷(ー6)から先に計算してるね。
右の式は(ー6)×2から先に計算しているね。
どの計算を先にするかで答が変わるんだね。じゃあどっちが正解かわかる?
正解は左の式なんだ、なぜか?それは、乗法、除法の混ざった式の計算順番を思い出してみて。

すべてを”×”にして計算してみると答えは”8”になったね。これが正解なんだ。
今回みたいに暗算で計算できる問題をわざわざ、上の式みたいに①、②、③の順番で計算しないと
いけないかって言うとそうではないんだ。数学の計算をする上でのルールがあるのでそれを守れば
暗算でできるところは暗算でやっちゃっていいと思うよ。
そのルールっていうのが
乗法と除法の混ざった式は左から順番に計算する
これだけ、ここをしっかり覚えておこうね。
次は四則を含む式について学んでいこう。っとその前に少し寄り道
同じ数の積
同じ数の乗法を次のように表すこともできるんだ。

このように同じ数をかけた回数をその数字の右肩に小さく表示して○乗っていう言い方をするんだ。
その右肩に小さく表示しているものを指数っていうのも覚えておこうね。

負の数が混ざった計算ではこんな注意があるから気をつけようね。

これで、四則の含む計算にいけるね。
四則を含む計算
四則ってなにか覚えてる?
この記事の初めに話してた内容だから、忘れっちゃったかな?
四則って言うのは加法、減法、乗法、除法をまとめて呼ぶときにこの言い方をするんだ。
四則が混ざった式でも、乗法、除法であったようなルールがあるからまずそれを覚えよう。
計算の順序
①かっこ・指数から先に計算する
②乗法、除法を計算する
③加法、減法を計算する
①、②、③それぞれで、左から順に計算することも忘れちゃダメだよ。
また、a x ( b + c )のような式の場合、a はそれぞれ、 b と c にかけられている事になるんだ。
これを分配法則と呼ぶんで覚えておいてね。
ようするに a x ( b + c ) = a x b + a x c ってなるんだ。

ちなみにこの式の中に(ー6+5)×4ってあるけど、これを分配法則で解くこともできるよ。

答えはどちらで計算しても、同じになることが確認できたね。
ここまでが、正の数、負の数の計算だよ。ほんとの基礎となる部分だから、しっかり理解しておこう。
ここまでの記事が良かったと思ったらここをクリックしてね。
コメントもくれるとうれしいな。





コメント