どうもこんにちは、DKです。
このブログでは中学数学の基礎を学びたい人向けに
各単元の基礎の解説を行っています。
今回は中学3年生で習う多項式の展開の公式についてやっています。
多項式は4回に分けてるので他のブログを見たい人は こちら から
アクセスしてみてください。
1.展開の公式
前の章で解説したのは項が全てバラバラなときの多項式と多項式の積ってことだったんだけど
今度は、多項式に同じ項があった場合を考えていきますね。
それっていうのが、\((x+a)(x+b)\)のような式だね。
どちらの多項式にも「\(x\)」が含まれているよね。
これを\((x+a)(y+b)=xy+bx+ay+ab\)に当てはめて考えてあげると
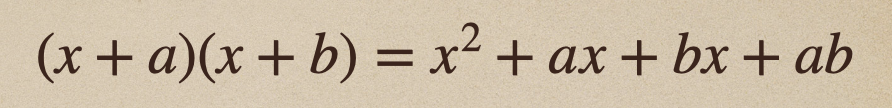
ってなるよね。
ここで、\(ax\)と\(bx\)を\(x\)でまとめてあげることができるよね。
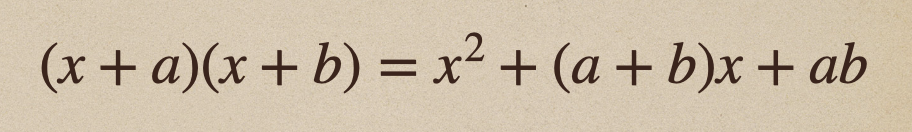
こうして見るとあることが気がつくよね。
それっていうのが、右辺の\(x\)の係数っていうのは
\(a\)と\(b\) の和で、定数項っていうのは、\(a\)と\(b\) の積になっているよね。
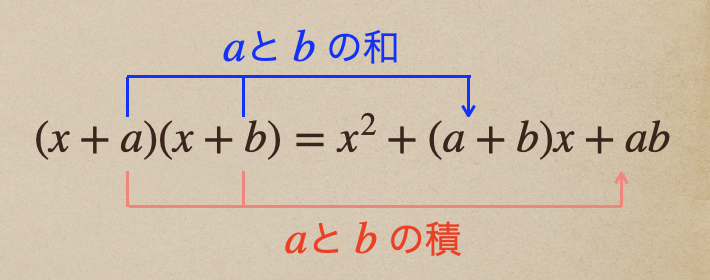
これが公式になっていて、展開の公式①になるんだね。
こういった形の式を見たときは、\(a\) と \(b\) にあたる項を足す、かけるをして
展開してあげればいいってことだね。
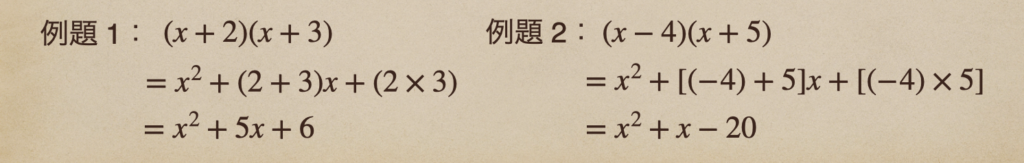
例題1は \(a\) を \(2\) 、\(b\) を \(3\) に置き換えて考えてあげて
\(x\) の係数を \(2+3\) してあげて、数の項を \(2×3\) をしているってことだね。
あとは、それぞれ計算してあげればいいってことだね。
例題2も考え方は一緒なんだけど、\(-4\) となっているところを \(a\) として
見てあげる必要があるので注意しておこう。
あとは、足す、かけるをして計算してあげればいいね
他にも、あと3つ公式としてはあるんだけど、それっていうのが
②\((x+a)^2\)、③\((x-a)^2\)、④\((x+a)(x-a)\)になるんだ。
それぞれ、確認していくけど考え方としては展開の公式①と同じになるんだね。
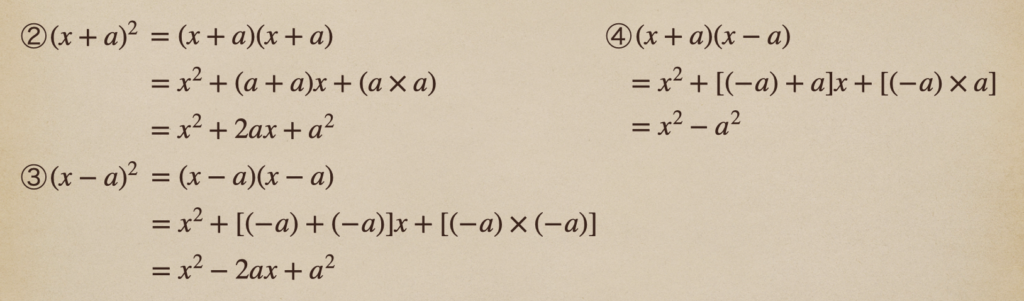
累乗している②や③は同じ多項式のかけ算になっているだけなので
それを解いてあげれば、展開の公式①に当てはめて計算することができるよね。
④も同じで展開の公式①を当てはめてあげればいいってことだね。
ただ、それぞれ、符号が違うので、\(x\) の係数の足し算では、\(0\) と
なってしまうので、\(0×x\)となって \(x\) がなくなるってことだね。
ここで出てきた解っていうのが、展開の公式になっているってことなんだね。
この展開の公式をまとめがこれになるよ。
【展開の公式】
①\((x+a)(x+b)=x^2+(a+b)x+ab\)
②\((x+a)^2=x^2+2ax+a^2\)
③\((x-a)^2=x^2-2ax+a^2\)
④\((x+a)(x-a)=x^2-a^2\)
この「展開の公式」っていうのは「乗法公式(じょうほうこうしき)」って
言い方をすることもあるよ。
今度は、この展開の公式を活用した例を見ておこう。
2.いろいろな式の展開
展開の公式を理解したところで、この公式っていうのも使うべきところで
活用できてこそ、自分のものにしていくことができたと言えるんで
ここでは、いろんなパターンの式を例に展開の公式を使って展開していってみよう。
(1) \((3x+3)(3x-4)\)
(2) \((3x+4y)^2\)
(3) \((a+b+2)(a+b+4)\)
この(1)〜(3)を展開するってなった場合、みんなならどんな風に展開していくかな?
分配法則で、それぞれをかけ合わせて計算していくこともできるよね。
けど、それだと、途中の計算式が複雑になったりしてしまうよね。
こんな時には、展開の公式を活用して、簡単に計算を行なっていけるんだね。
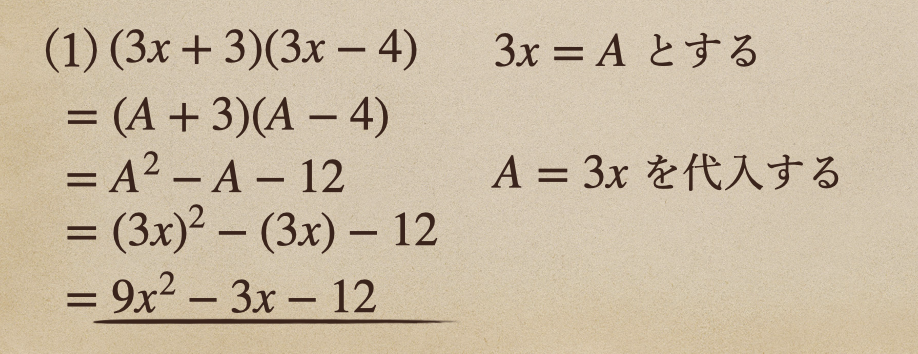
(1)であれば、そのまま、展開の方式を当てはめていくこともできるんだけど
\(3x\) を違う、文字に当てはめることで展開の公式をわかりやす
活用しているんだね。
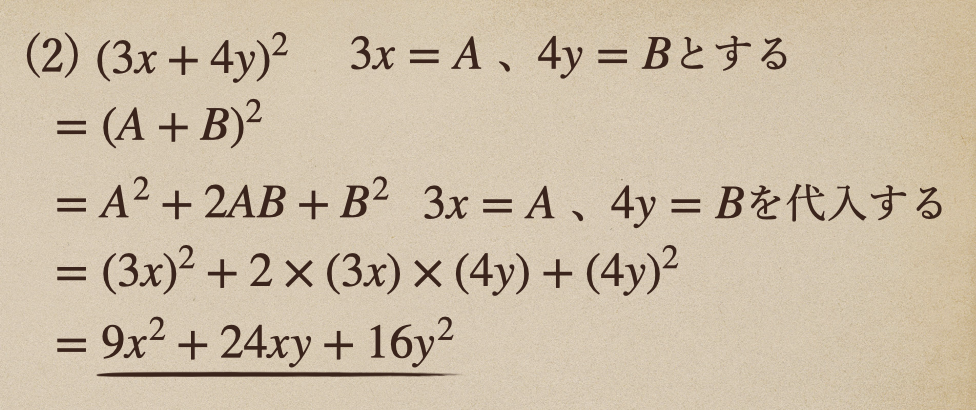
これも、(1)と同様で、複雑な式を少しでも、簡単にしてあげてから
展開を行なっているってことだね。
この(2)も、もちろん、そのままでも展開することはできるので
自分の力に合わせた解き方で解いていこう。
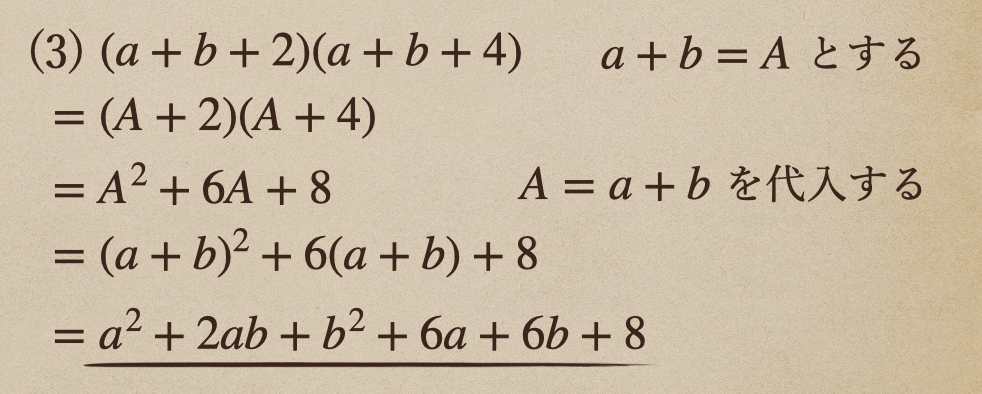
(3)の問題は、共通する式の\((a+b)\)を一つの文字\(A\)としているんだね。
こうすることで、展開の公式に当てはめて展開していくことができるんだね。
こんな風に、置き換えて考えることで展開の公式を使って、展開をスムーズに
することができる場合もあるってことを覚えておこう。
今回は、ここまでになります。
ここまでの記事が良かったと思ったらここをクリックしてね。
質問なんかがあった場合はコメントにお願いします。
では、またさようなら。



コメント