どうもこんにちは、DKです。
このブログでは中学数学の基礎を学びたい人向けに
各単元の基礎の解説を行っています。
今回は中学3年生で習う多項式の展開の公式についてやっています。
多項式は4回に分けてるので他のブログを見たい人は こちら から
アクセスしてみてください。
1.因数分解
この因数分解は読み方を「いんすうぶんかい」って言うんだけど、これって言うのは
【因数分解】
1つの多項式を単項式や多項式の積の形に表す
ってことになるんだね。これがどう言うことかと言うと
\(x^2+3x=x(x+3)\)
\(x^2+6x+8=(x+2)(x+4)\)
って具合にすることだね。これって言うのが
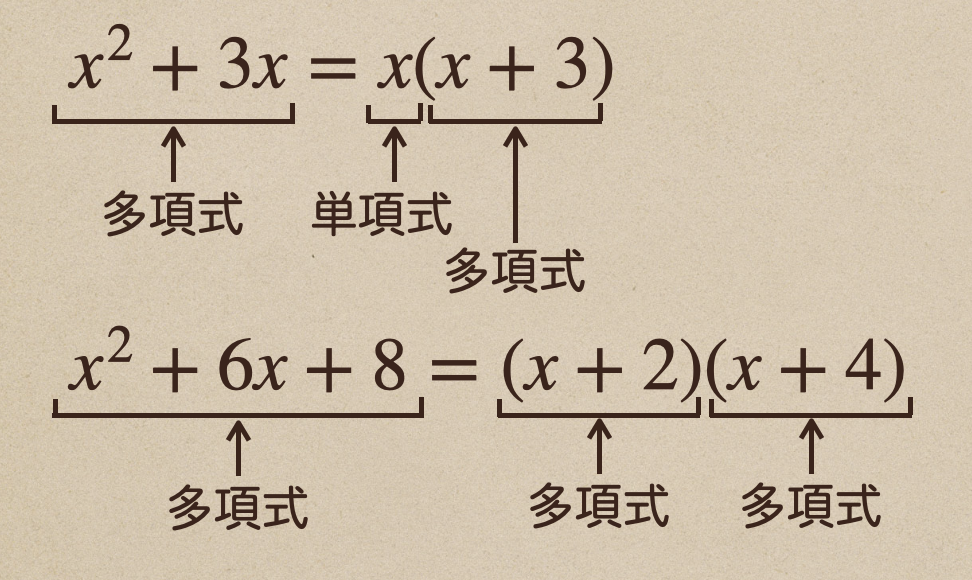
多項式だった式を、単項式×多項式の式や、多項式×多項式の式にしているってことなんだね。
そして、この1つの式を単項式や多項式の積の形に表すときに
その1つ1つの式や数のことを、もとの式の因数(いんすう)って言うんだね。
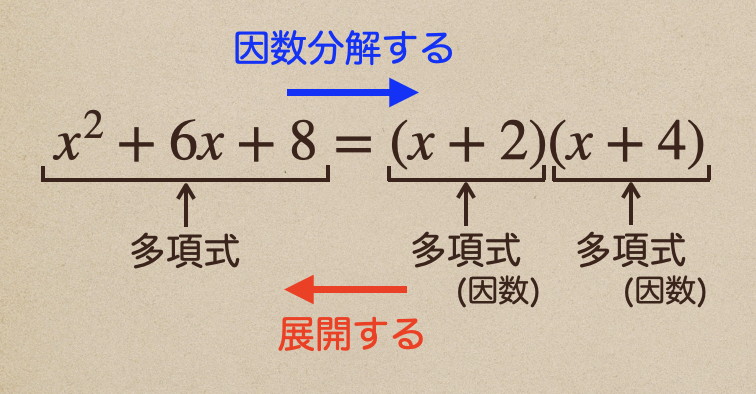
多項式を因数の積の形に表すことを、その多項式を因数分解するっていう言い方をするよ。
だから、「展開する」って言うのと「因数分解する」って言うのは、反対の意味に
なっているってことなんだね。
多項式の各項で共通の因数があった場合は、分配法則を使って共通な因数をかっこの外に出して
因数分解することができるんだね。
\(ax+ay=a(x+y)\) \(a\):共通因数
この因数分解には決まり事があって、因数分解する時っていうのは
共通因数を残らず外に出してあげる必要があるんだね。
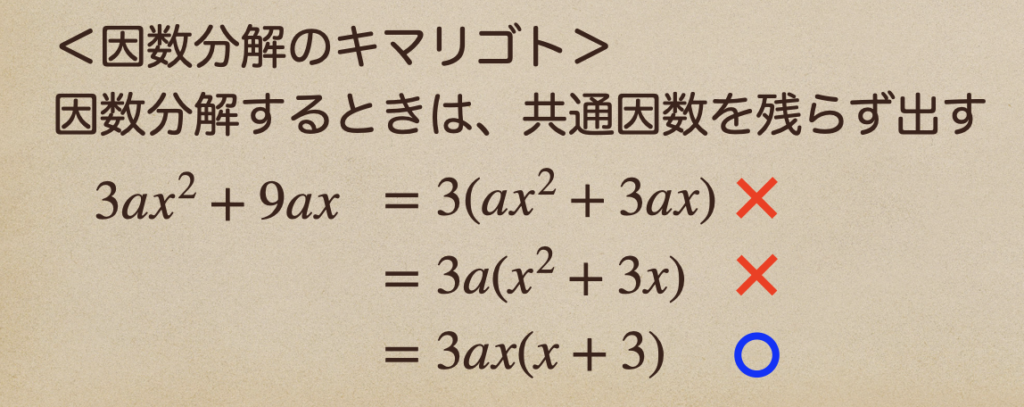
2.公式による因数分解
因数分解にも公式があるんだけど、これっていうのは、前の章で解説を行なっていた
展開の公式の逆ってことになるんだね。
\((x+a)(x+b)\)の展開の公式は\(x^2+(a+b)x+ab\)ってことだよね。
逆に\(x^2+(a+b)x+ab\)を因数分解すると、\((x+a)(x+b)\)になりますよって
ことが言えるんだね。

これは、多項式\(x^2+(a+b)x+ab\)があって
\(x\)の係数は\(a\)と\(b\)の和になって、数の項は\(a\)と\(b\)の積に
なっていた場合、\((x+a)(x+b)\)と因数分解できるってことになるんだね。
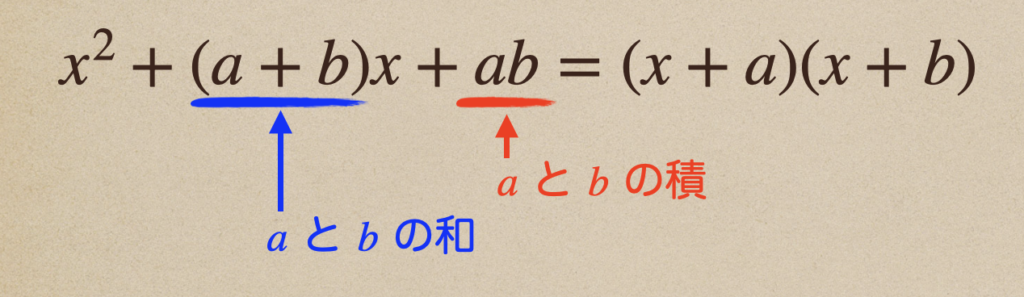
これが、因数分解の公式①’になるんだね。
この因数分解のやり方っていうのを見ていくね。
[例題]\(x^2+9x+18\)
これを因数分解しようとすると、まず「かけて\(18\)」になる値をみて
その値が「足して\(9\)」になる値を求めてあげればいいんだね。

①→②→③の順に考えていってあげればいいってことだね。
慣れないうちはむずかしいってなるかもしれないけど、慣れない間は書き出して
組み合わせを探してあげよう。慣れてきたら、頭の中で、かけ算の組み合わせを
考えてあげて、その組み合わせの和が\(x\)の係数になるものを探してあげるように
していこう。
因数分解の公式は、展開の公式と同じだけあって、それっていうのが。。
【因数分解の公式】
①’ \(x^2+(a+b)x+ab=(x+a)(x+b)\)
②’ \(x^2+2ax+a^2=(x+a)^2\)
③’ \(x^2-2ax+a^2=(x-a)^2\)
④’ \(x^2-a^2=(x+a)(x-a)\)
ってことになるんだね。展開の法則を覚えてしまっておけば、その逆として
覚えていけるんだね。
因数分解の公式を例題で確認してみよう。
例題 1 \(x^2+8x+16\)
これを因数分解してみよう。この例題1が公式のどれになるのかっていうのを
考えても、パッとは出てこないよね。
なので、この場合は、まず公式①の\(x^2+(a+b)x+ab=(x+a)(x+b)\)で
考えてあげよう。そうすると。。
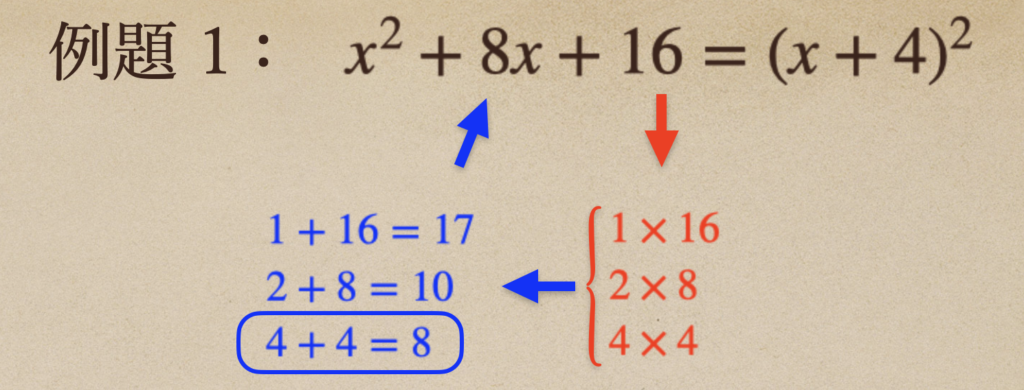
数の項の「\(16\)」をかけて\(16\)になる組み合わせを考えてあげて
その組み合わせを足したときに \(x\) の係数の「\(8\)」になるものを
探してあげて、例題1では、\(4×4=16\)、\(4+4=8\)があったよね
なので、答えは \(x+4)^2\) になるってことだね。なので公式②を
使ったってことになるんだね。
この問題が公式②を使って解きなさいってなっていたら簡単なんだけど
問題はそんなにやさしくないよね。
こういった問題では、まずは公式①を使いながら因数分解していくことを
いいよね。
慣れてくれば、数の項の平方根が正数となる場合に、その2倍が
\(x\)の係数になるかっていう解き方をしていくのもありだね。
例題2 \(x^2-6x+9\)
この問題も同じく公式①で考えていくと。。
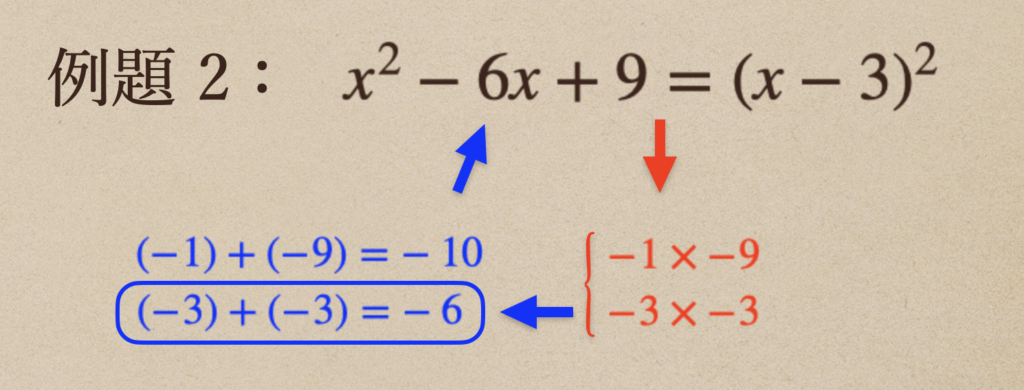
この例題では\(x\)の係数が「\(-6\)」となっているので
数の項の「\((+)9\)」の積は負の符号で考えてあげて
\((-3)×(-3)=9\)、\((-3)+(-3)=-6\)の組み合わせってことで
答えは、\((x-3)^2\)になるってことだね。
例題3 \(x^2-81\)
この例題では\(x\)がないよね。この場合はわざわざ公式①を使わなくても
公式④ってことがわかるよね。この場合で、公式①を使って考えることはできて
\(x\)がないってことは、\(0×x\)となっているってことなんだね。こうやって考えると。。
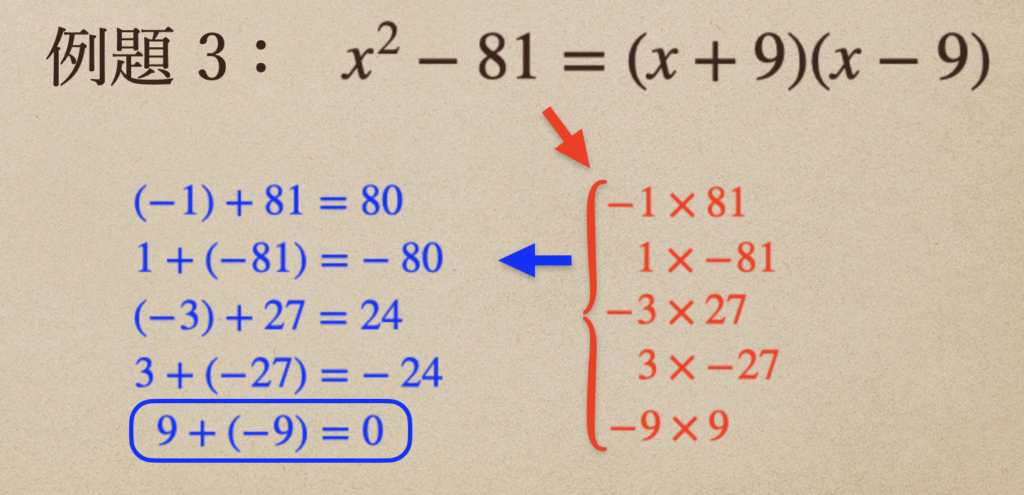
\((+9)×(-9)=-81\)、\((+9)+(9)=0\)の組み合わせってことが求められて
答えは\((x+9)(x-9)\)になるってことだね。
因数分解では、わざわざ公式通りに因数分解する必要はないので
まずは、公式①をしっかり使いこなせるようになってから
他の公式となるパターンっていうのを問題を解きながら身につけて
いってもらえればいいかなと思います。
3.いろいろな式の因数分解
いろいろな形の式を因数分解する場合を例題を使って考えてみよう。
(1)共通な因数がある多項式の因数分解
例題1 \(3ax^2+6ax-72a\)
こんな式があった場合、因数分解の公式も当てはめられずに
わからなーいってなっちゃうかもしれないんだけど
この式をよく見てみると、すべての項が「\(3a\)」で割り切れるよね。
これを解いていくと。。
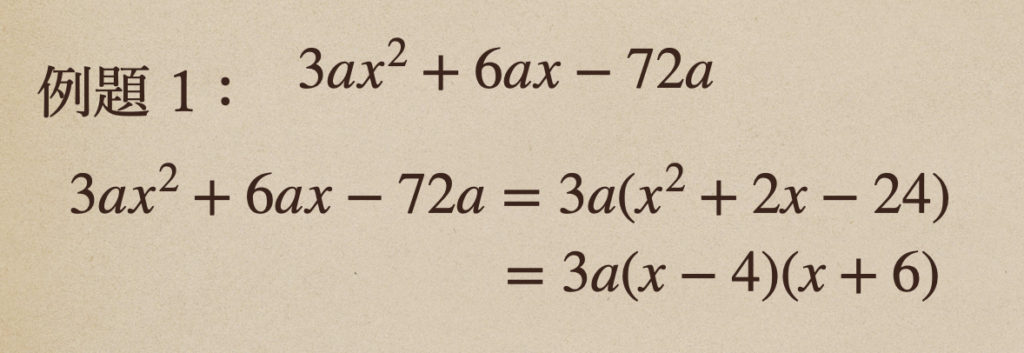
\(3a\)を外に出してあげることで、カッコの中で因数分解の公式で
解くことができる式ができたよね。あとは、カッコの中も因数分解して
してあげて、\(3a(x-4)(x+6)\)ってところまで因数分解してあげることが
できたね。こんな風に、すべての項に共通してある因数を先に因数分解することで
さらに細かく因数分解することができるんだね。
(2)公式を使ういろいろな因数分解
例題2 \(x^2+7xy+12y^2\)
\(x\) と \(y\) が使われた式ではあるんだけど
\(x^2+(3y+4y)x+(3y×4y)\)となっていることがわかるよね。
これは公式①’の\(x^+(a+b)x+ab=(x+a)(x+b)\)と同じ形になっているんだね。
これを解いてあげると。。
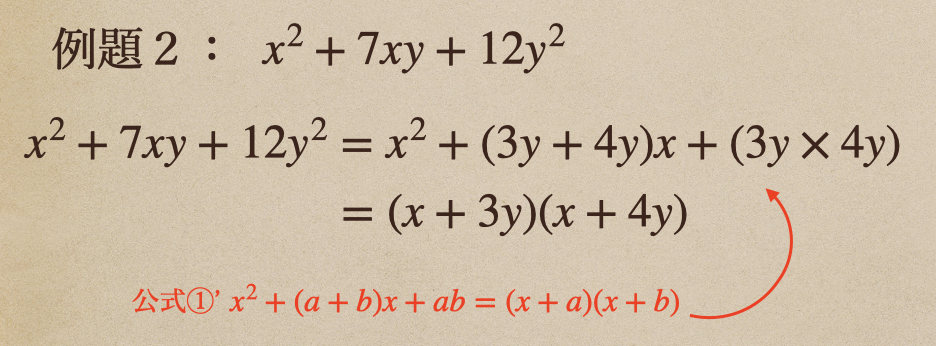
こんな風に因数分解することができるんだね。
例題3 \(9x^2-24xy+16y^2\)
\(x^2\) の係数が\(9\)となっているんだけど、これも
見方を変えてあげると、\((3x)^2-(2×3x×4y)+(4y)^2\)となっているんだね。
これは公式③’の\(x^2-a^2=(x+a)(x-a)\)と同じでみることができて。。
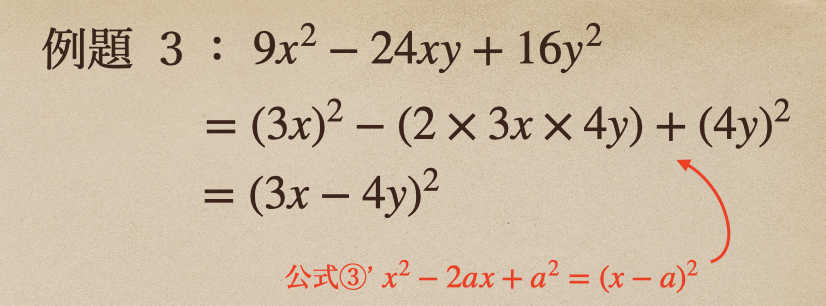
多項式が複雑になったとしても、考え方としては同じことで
そこをしっかり理解できていれば、こういった問題も解いていくことができるんだね。
例題4 \(25x^2-9y^2\)
この問題も考え方は同じで、まずこの多項式のそれぞれの係数を
OOの2条になっているかを見てあげるんだね。そうすると、この多項式は
\((5x)^2-(3y)^2\)ってなっていることがわかるよね、
この形っていうのが、公式④’\(x^2-a^2=(x+a)(x-a)\)でみてあげることが出来て。。
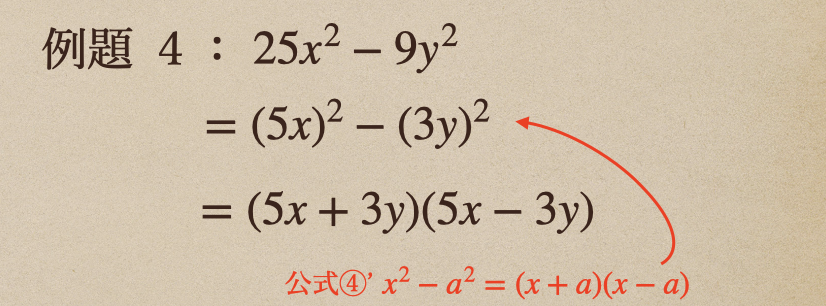
多項式を置き換えることで、どの公式と同じ形にしてあげることが
できるかどうかって言うのを見て解いていくようにしよう。
次にもう少し複雑な多項式を因数分解する方法っていうのを見てみよう。
(3)多項式を1つの文字に置きかえる因数分解
どういうこと?ってなっちゃうと思うので、例題をみて考えていこう
例題5 \(xy-4x+2y-8\)
例題1では、多項式全体を単項式でくくってあげることで
因数分解ができたよね。ただ、この問題では、それができないよね。
こういった場合は、細かく因数分解してみるんだね。
\(xy-4x+2y-8=x(y-4)+2(y-4)\)こんな風にすることができるね。
ここで、因数分解されたカッコの中が同じ\((y-4)\)になっているよね。
この\((y-4)\)を\(A\)として考えてあげて、式を解いていくと。。
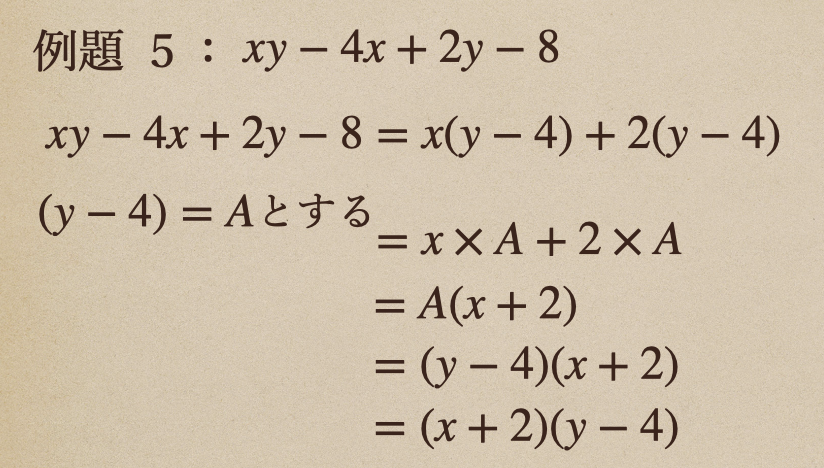
同じ多項式があれば、こんな風に因数分解することができるってことなんだね。
この例題の場合は、同じ多項式を作ってあげることができるかっていうのが
ポイントになってくるので、どんなくくり方をすればいいのかっていうのを
考えていく力は必要になるので、似たような問題をいくつも解いてあげることで
早く、的確に因数分解していくことができるようになるよ。
今回は、ここまでになります。
ここまでの記事が良かったと思ったらここをクリックしてね。
質問なんかがあった場合はコメントにお願いします。
では、またさようなら。



コメント