どうも、こんにちはDKです。
今回は文字式の基礎についてやっていくね。
小学校までは、全て実数だけの計算で、答えも数字で表されてきたけど
中学からはここで教える文字式で式が表されたり、答えも文字式で表されたりするんだ。
ここも、しっかり基礎を身につけてわからないをなくしていこうね。
動画でも解説しているよ。↓↓↓ ※音が出るので注意。
数量を文字で表す
まずは、今までの計算をする場合、答えを表すための数字が出てきてたと思うんだけど
これからは、任意の数字って言うのが、文字で表すことになって、文字を使って式を
作る必要があるんだ。実際にやってみよう。
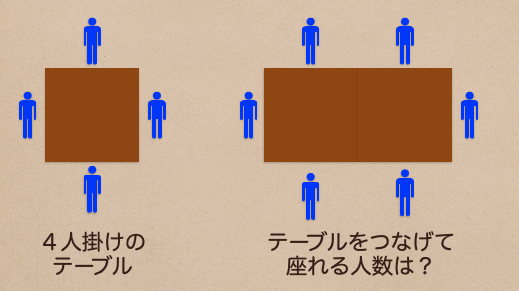
1テーブル4人で座れるとした場合、このテーブルをつなげて座れる人数を計算してみよう
2テーブルにした場合は?ってなった時、6人座れることになるよね。
この場合、図にあるように数えればすぐに人数もわかるけど
じゃあ、9テーブルになった時に座れる人数は?ってなった時にすぐに答えられるかな?
図のようにテーブル9台並べて人数を数えればいいんだけど、時間かかっちゃうよね
こう言う時はテーブルの数によって、何人座れるかを考えるんだね。
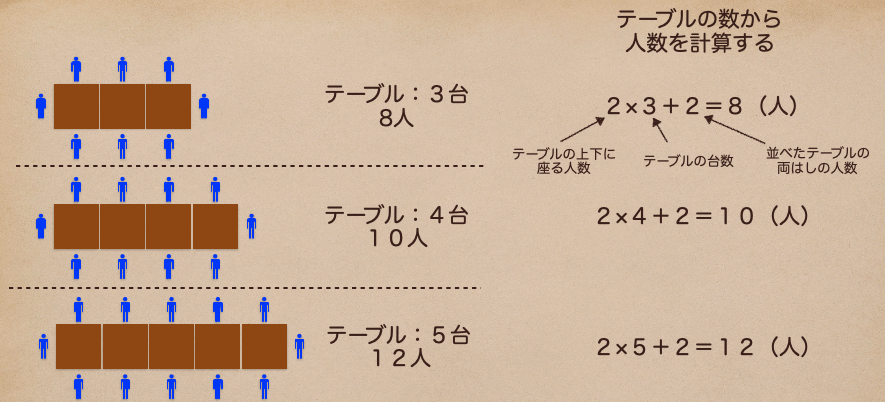
テーブルの台数を3台、4台、5台と並べた時に座れる人数を考えた時に右側に書かれてる式で
計算することができるよね。
ようするに、テーブルの台数と座れる人数はこんな式で計算できるってことだね。
2×(テーブルの台数)+2
ここで、テーブルの台数がa台とした時には上の式の(テーブルの台数)にaをかえて
2×a+2
と表すことができるね。じゃあ、さっきのテーブル9台の場合を考えてみようか。
2×9+2=20(人)
テーブル9台の時に座れるのは20人ってすぐに出てきたね。
この”2×a+2”の式が文字を使った式ってことになるんだ。
こんな感じで、色々な数量を文字式で表すことができるんだ。

①求めたい数値は全体の重さ
→a×12+400の”a”に数値を当てはめることで求めることができる
②求めたい数値はおつり
→1000ーb×5の”b”に数値を当てはめることで求めることができる
③求めたい数値は代金
→100×a+150×bの”a”と”b”に数値を当てはめることで求めることができる
文字式はわかっていない数量に文字を置いて、文字に数値を当てはめることで
求めたい部分を計算すことができるんだね。
次は文字式の表し方についてやっていくね。
文字式の表し方・式の値
文字式を書く場合には、書き方の約束ごとがあるんだ、ここではそれをしっかりと覚えておこう。
文字式の表し方の約束ごと
①かけ算の記号”×”は書かない
②文字と”1”や”−1”の積では、”1”を書かない
③文字と数の積では、数を文字の前に書く
④文字だけの積ではアルファベット順に書く
⑤同じ文字の積は指数を使って書く
⑥わり算は”÷”を使わずに、分数(逆数)で書く
約束ごととしてはこの6つになるんだ、ただ、気をつけることは文字を使った場合に限るから
注意しよう。6つの約束ごとがどう言うことかは、下で解説するね。

こんな感じで、文字を使った式は”×”や”÷”を使わずに表して、式を簡単にすることが約束ごとに
なるんだね。慣れないうちはついつい”×”や”÷”を書いて表してしまうかもしれないけど、この書き方は
しっかり慣れていこうね。
次に文字式の文字に数をあてはめて、計算する式の値について説明していくね。
まずは言葉を覚えておこうね。
式の値
式の中の文字に数をあてはめることを代入と言う。
文字の数を代入した数のことを文字の値と言う。
代入して求めた結果を式の値と言う。
この”代入”や”値”ってところはよく使われることだからしっかり覚えておいてね。
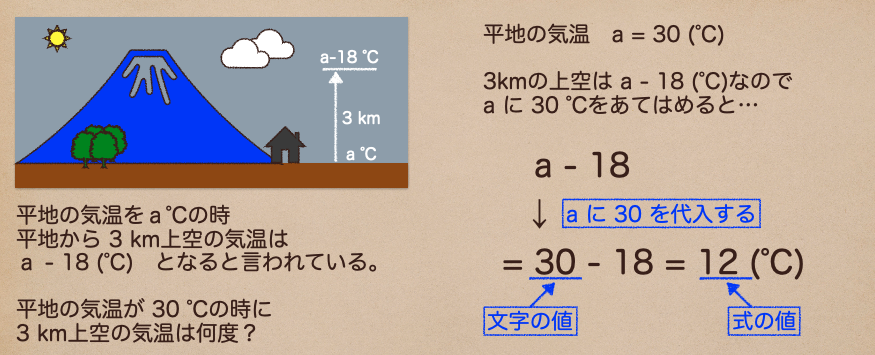
この場合、aの値が30のとき、a-18の値は12という言い方をするんだ。
文字が2つ以上あった場合でも、それぞれの文字の値がわかっていれば、式の値は計算できるよね。
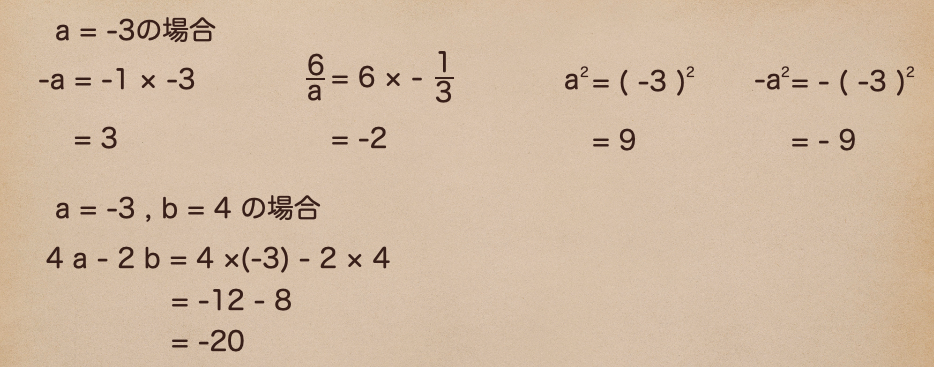
ここで、前の単元でやった正の数、負の数も関係して、正しく計算して正の符号、負の符号を
間違えないようにする必要があるから、正の数、負の数がまだ自信ない人はこっちを見てみてね。
文字式の加法、減法
加法、減法は正の数、負の数でも出てきたよね?
加法は足すこと、減法は引くことだったよね。この加法と減法を文字式でも使ってみよう。
と、その前に少し言葉を覚えておこうね。

項と係数だね、テストにもよく出てくるし、問題文にもよく出てくる言葉になるのでしっかり覚えておこうね。
問題文では「次の式の項の内、、、」や「係数が3とした場合、、、」みたいな使われ方するから
項ってなだっけ?係数ってどれだっけ?みたいに迷わないようにしていこうね。
ちなみに、\( x \) の係数は 1 になるよ。
じゃあ、もう少しだけ言葉を覚えていこうね。

一次の項、一次式が何かわかったかな?
特にこれから二次の項、二次式、多項式なんて言葉も出てくるから、どう言ったものが一次式なのかをしっかり理解して覚えていこうね。もう少しだけ、詳しく説明しておくね。
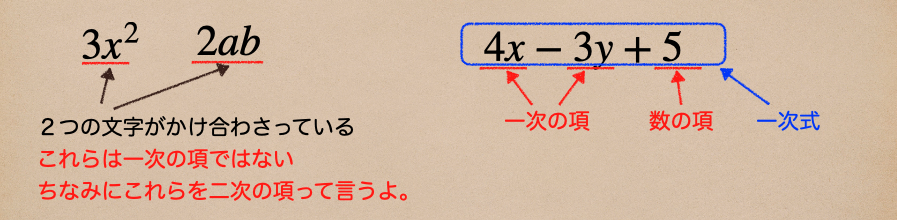
少しは、イメージできたかな? ちなみに、二次の項はもう少し先でまた、出てくるので
今回は、こんなのがあるんだ、ふーんくらいで流しといてくれたらいいからね。
今回、覚えるのは一次の項、一次式だよ。
じゃあ、文字式の加法と減法についてやっていくね。
文字式で出てくる加法と減法は単純に式を簡単にするってことになるよ。ようするに。。
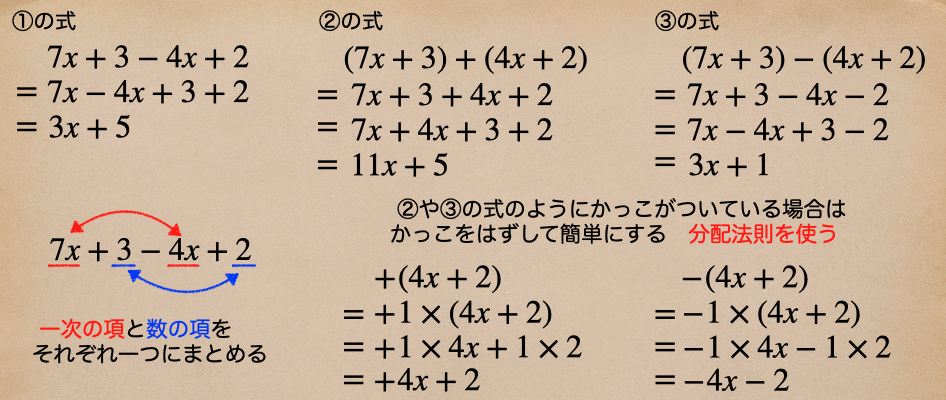
①の式の場合、文字を使った一次の項 ( \( 7x \),\(-4x\) )と数の項 ( 3 , 2 ) を一つにまとめて式を
簡単にするってことになるんだ。
気をつけておきたいのはかっこを使った式を簡単にする場合で、②や3の式の場合だね。
かっこの前の符号が正か負かによってかっこをはずした時の式が変わってくるからその後の
答えも大きくちがってくるよ。
かっこをはずして計算する場合に、自信がないようなら上の図のように分配法則によって
かっこの前の符号がかっこの中の数にそれぞれかけられるんだけど
それは符号だけをかけるのでなくて−1や+1がかけられているってことになるので
それをしっかり書き表して計算すれば、間違いも少なくなるんじゃないかな。
文字式と数の乗法、除法
ここでは文字式と数の乗法(かけ算)と除法(わり算)を教えているよ。
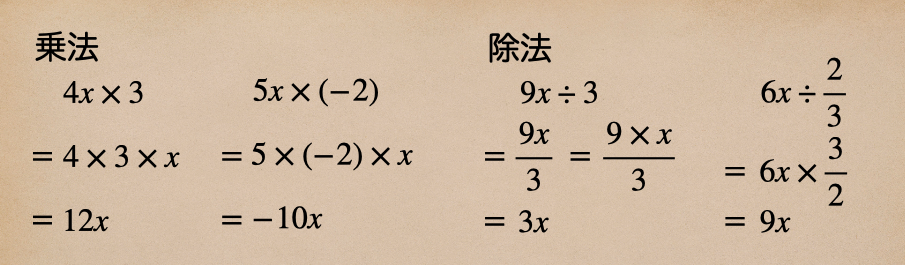
文字式と数の乗法、除法の場合は、数の方を計算するだけになるよ。
簡単だよね、だけど、項が2つ以上の式に数をかけたり、わったりするときは注意が必要だよ。
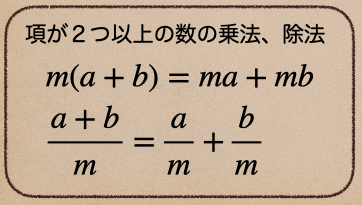
こんな感じでそれぞれにかけたり、わったりしないといけないんだ。
簡単な例題で式を簡単にしてみるよ。
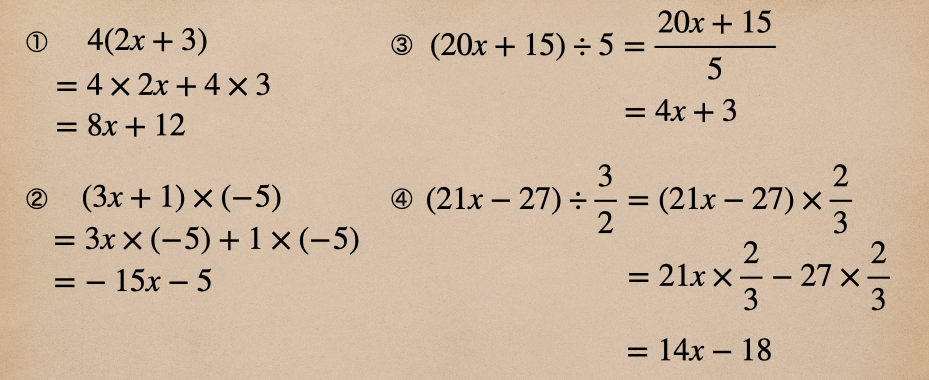
①、②は乗法、③、④は除法の例題になるよ。
どっちもかっこの中をかけたり、わったりしてるよね。この計算の仕方をしっかり身につけないと
正しく計算できなくなっちゃうからね、気をつけようね。
関係を表す式
今度は、関係を表す式をやっていくね。
ここでも、まずは言葉を学んでいこう。まずは下を見てみて。

りんごの重さの合計は a + b と表すこともできるし、500gとも言えるよね?
こんなふうに同じことが言える関係を等しい関係の式として=(イコール)で表すことが
できるんだ。この a + b = 500 を等式(とうしき)と言って、等式の左側の式を
左辺(さへん)、右側の式を右辺(うへん)と言うんだよ。
そして、両方を合わせて両辺(りょうへん)って言うんだ。

等式は左辺と右辺が等しい場合を指しているんだけど、もし2つのりんごの合計が500gより
重かった場合、どのように表すのかな?または、軽かった場合どうやって表す?

左辺と右辺の関係が等しくない(どちらかが、大きい/小さい関係)のことを
不等式(ふとうしき)って言うよ。
この大きさを表す記号 ”<”、”>”を不等号(ふとうごう)って言うんだよ。
式の読み方は左辺が大きい場合 a + b > 500 を「 a + b 大なり500」
左辺が小さい場合 a + b < 500 を「 a + b 小なり500」って言い方をするんだよ。
他にも ≧:大なりイコール、≦:小なりイコールっていう不等号もあるんだ。
これは、左辺と右辺が等しいかそれより大きい、小さいってこと言ってるんだね。
不等号の呼び方
<:小なり(しょうなり)
>:大なり(だいなり)
≦:小なりイコール
≧:大なりイコール
大小の関係を表すときの言葉の使い方によって、使う不等号がちがってくるから
もう一度、おさらいしておこう。
〜より:含まない ・・・< , > で表す
〜未満:含まない ・・・< , > で表す ※未満:小さいことを表す
〜以上(〜以上):含む ・・・≦ , ≧ で表す
ここの〜より、〜未満、〜以上などをしっかり理解しておかないと不等式を書くときに
正しい、不等号を使って式を書くことができないから自信が持てないようなら、ここでしっかり
学んでいってね。
以上が文字式についてになるよ。次はいよいよ方程式だよ。数学と言えば、方程式って言うくらい
大事なところになるからね。方程式を学ぶには、ここの文字式をしっかり理解していないと
方程式も理解できなくなってしまうから、まだまだ、自信が持てないようならじっくり時間を
かけて理解していこうね。
ここまでの記事が良かったと思ったらここをクリックしてね。
コメントもくれるとうれしいな。




コメント