どうも、こんにちはDKです。
前回の投稿では中学3年生で習う「2次方程式」について基礎をやっていてそこでは
2次方程式って何?ってとこから、2次方程式の解き方について解説をしていたので
今回は、2次方程式を利用した問題についてやっていきますね。
ようするに、2次方程式を使った文章問題ってことになりますね。
この2次方程式の利用では、問題から2次方程式を作ってそれを解いて解を求めてあげて
問われている答えを導き出すってことになるんですね。
なので、2次方程式の解き方っていうのをしっかり理解できていないと
問題から2次方程式が作れたとしても、その解を求めていくことができないってことに
なっちゃうので、2次方程式の解き方についてまだ、わからないなー、不安だなーって
思う人は、2次方程式の基礎をもう一度、読み返してみてください。
↑「2次方程式の基礎」をクリックするとそのリンクに飛べるよ。
中学生では2次方程式の利用には大きくまとめると2つの問題があって
1つ目が『数に関する問題』と2つ目に『図形に関する問題』になるんだね。
これらを応用して問題が作られていることがほとんどになるんだ。
一つずつ見ていきますね。
[1]数に関する問題
数学といえば、これ!!というほどにこの数に関する問題はよく出てきて
この2次方程式に限らず、多項式、連立方程式なんかでもよく使われているんだね。
ここでは、2次方程式に関わる数に関する問題を例題を使って解き方の流れを
見ていきますね。
【例題】大小2つの正の数があり、その差は3で積は40になる。
この2つの数を求めよ。
シンプルな問題になっているんだけど、ここから2次方程式を作っていくってことですね。
まず、わかっていることを整理すると
①大小2つの正の数の差は3となる。
②大小2つの正の数の積は40となる。
ってことですね。じゃあ、ここからわかっていない大小2つの正の数っていうのを
\(x\)を使って表すとすると。。
小さい数を\(x\)とすると、大きい方の数っていうのは①にあるように
差が3ってことなので、\(x+3\)として表すことができるってことですね。
①から 小さい数:\(x\)
大きい数:\(x+3\)
次に②の大小2つの積が40になるってことで
大小の積ってことなので、\(x\)と\(x+3\)の積ってことなので
\(x×(x+3)\)と表すことができて、これが40になるってことですよね
なので、\(x(x+3)=40\)となるってことですね。
あとはこれを、解いてあげて。。
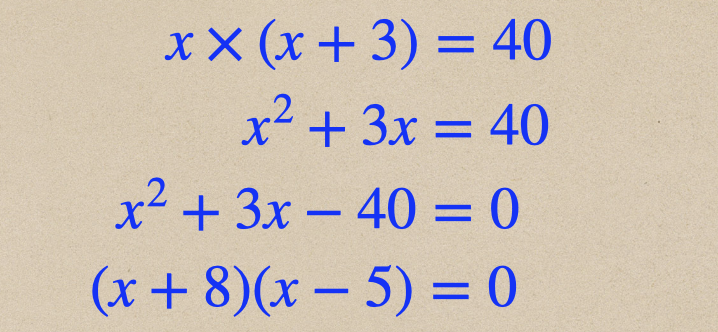
作ってあげた等式を展開してあげて、2次方程式\(ax^2+bx+c=0\)の形にして
そこら2次方程式を解いていってあげればいいてことですね。
今回の例題の場合、因数分解することができて\((x+8)(x-5)=0\)となるので
ここから、それぞれ\((x+8)=0\)と\((x-5)=0\)として考えてあげて
\(x\)の値を求めてあげるんだね。

これで、\(x\)の値が\(-8\)と\(5\)と求めることができたので
この解が答えかっていうと、そうではないんですね。
2次方程式の利用の場合は、解が求められたら
この2つの解から今回の問題が当てはまるのかって言うのを見てあげていく必要があるんだね。
今回の問題では大小2つの数っていうのは正の数ってことだったよね。
このことから、2次方程式の2つの解である\(x=-8\)と\(x=5\)から
負の数である\(x=-8\)はこの問題に適していないってことが言えますよね。
なので、この問題では、\(x=5\)だけが求めるべき数ですよってことになるんですね。
で、問題で求められているのは大小2つの正の数を求めるってことだったので
小さい数は\(5\)で大きい数の方は、\(x+3\)ってことだったので\(x+3=5+3=8\)となって
これが答えになるってことですね。

これで、答えを求めることができたってことになりますね。
ポイントとしては
2次方程式で求めた解っていうのは
ほとんどの場合が2つの解が求められることになるが
その2つともが、その問題の答えになるとは限らない
ってことなんだね。
[2]図に関する問題
こっちでも同じように例題を使って解き方を見ていってみよう。
【例題】ヨコよりタテの方が長い長方形がある。
この長方形の周の長さは\(26 cm\)で面積は\(42cm^2\)である。
この長方形のヨコ、タテの長さを求めなさい。
この問題でも、わかっていることを整理すると
①ヨコよりタテの方が長い・・・ヨコ<タテ
②周の長さが\(26cm\)・・・(ヨコ×2)+(タテ×2)=26
③面積が\(42cm^2\)・・・ヨコ×タテ=42
ってことですね。ここで、求めたいヨコの長さを\(x\)として考えてあげると
タテはどのように表すかっていうと整理した②(ヨコ×2)+(タテ×2)=26から
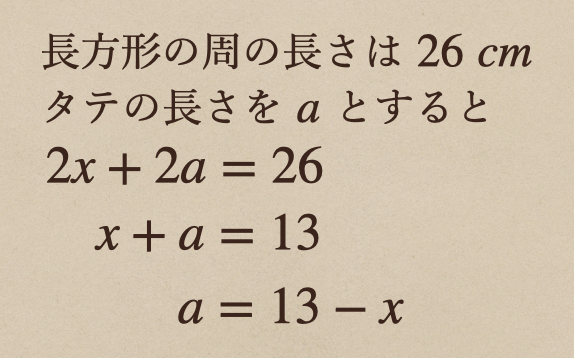
タテは\(13-x\)として表すことができるってことですね。
なので、ヨコ:\(x\)
タテ:\(13-x\)
次に③の面積が\(42cm^2\)ってことで、ヨコ×タテ=42ってことから
\(x×(13-x)=42\)となって、これを展開して2次方程式の形に直してあげると
\(x^2-13x+42=0\)となってこれを解いていってあげればいいってことですね。
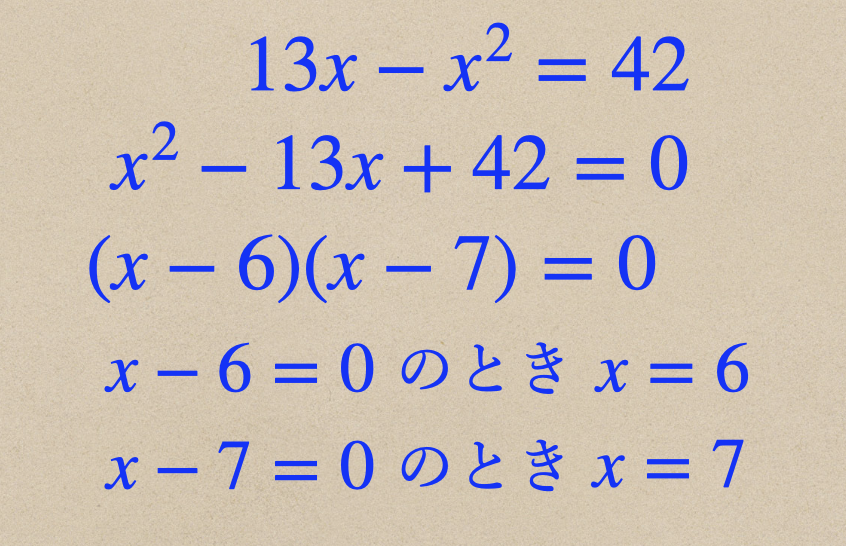
解いてあげると因数分解できて、\(x\)は\(6\)と\(7\)になったので
あとは、この解が問題に適しているかどうかっていうのを
見ていってあげればいいってことですね。
まず、\(x=6\)のときを見てみると、タテは\(13-x=13-6=7\)となるので
ヨコ:\(6cm\) タテ:\(7cm\)となるので、これは①のヨコ<タテが
成り立っているので、\(x=6\)は適しているってことになりますね。
次に、\(x=7\)のときを見てみると、タテは\(13-x=13-7=6\)となるので
ヨコ:\(7cm\) タテ:\(6cm\)となって①のヨコ<タテが成り立っていないので
\(x=7\)は成り立っていないってことになりますね。

これで、この問題の答えは
ヨコ:\(6cm\) タテ:\(7cm\)
となるってことですね。
ちなみに、今回の問題ではヨコ<タテと言っていたんだけど
どちらが長いと問題で言っていなければ答えは
ヨコ:\(6cm\) タテ:\(7cm\)もしくはヨコ:\(7cm\) タテ:\(6cm\)
と答えが2つになって来るんだね。
こういった、答えかがを2つになったりすることもあるので
問題をしっかり読んで、問題に適したものになっているのかを確認していこう。
[3]いろいろな問題
前の項で解説した「数に関する問題」と「図形に関する問題」っていうのが
形を変えて、2次方程式の利用として問題を出題されることが多いね。
他にも「物体の落下に関する問題」であったり、「関数のグラフに関する問題」なんかもあるね。
これらに共通してこの2次方程式の利用に出てくる文章問題っていうのは
解き方があって、それって言うのが
①どれを\(x\)にするかを決める
②数量の等しい関係を見つけて2次方程式をつくる
③2次方程式を解いて、解を求める
④その解が問題の条件に適しているかを確認する
ってことなんだね。
ポイントは『②数量の等しい関係を見つけて2次方程式をつくる』で
ここで間違えてしまうと、答えが求められなくなってしまうので特に
丁寧に、問題を読んで行くことが大事になってくるね。
あとは、『④その解が問題の条件に適しているかを確認する』ってところも
重要で、この2次方程式の利用における文章問題で導き出した解っていうのは
求められた2つの解が必ずしも、その問題の答えとならないってことなんだね。
これに気をつけて、問題を解いてあげるようにしていこう。
今回は、ここまでになります。
ここまでの記事が良かったと思ったらここをクリックしてね。
質問なんかがあった場合はコメントにお願いします。
では、また、さようなら。



コメント