どうも、こんにちはDKです。
今回は中学3年生で習う「関数\(y=ax^2\)」についての基礎をやっていきますね。
関数っていうのは、中学1年生でも習ったかと思うんだけど、今回は「\(y=ax^2\)」についての
基礎を説明していきますね。
この関数\(y=ax^2\)では、平方根や、2次方程式を活用して解いていく事になるので
平方根や2次方程式がわかっていないって人は、それぞの基礎をブログの方でも
公開しているのでそっちを見てください。
まずは、「関数 \(y=ax^2\)」って何?ってことから見ていきますね。
[1] 関数 \(y=ax^2\)
中学1年生で習った関数ってどんなものだったかと言うと
関数
一緒に変わっていく2つの数量 \(x\)と\(y\)について
\(x\)の値が決まるとそれに対応して\(y\)がただ一つに決まるとき
これ\(y\)は\(x\)の関数であると言う
ってことだったね。式で表すと\(y=ax+b\)って言うのが関数ってことになるんだね。
じゃあ、次の場合について、関数かどうかって言うのを見ていってみよう。

ボールが斜面を転がった時間( \(x\)秒後 )とその進んだ距離( \(y\) \(m\) )を表で
表すと次のようになった。

この表から、\(x\)の値が決まると、それに対応した \(y\)の値が決まっていることが
わかるよね。なので、このボールが斜面を転がったときっていのは、関数になっている
ってことが言えるんだね。
そして、これを文字式で表してあげると。\(y=2x^2\)となっているってことなんだね。
この関数は、2次式になっていて、この2次式の関数をここでは
「関数 \(y=ax^2\)」と言われているんだね。「関数 \(y=ax^2\)」ってどういうものっていうと。。

ってことなんだね。式を見てもそのままなんだけどこれが「関数 \(y=ax^2\)」ってことだね。
この章では、この「関数 \(y=ax^2\)」について、いろいろと解説しいきますね。
[2] 関数\(y=ax^2\)のグラフ
関数っていうぐらいなのでまずは、グラフについて見ていこう。
まずは、\(y=x^2\)のグラフを書いていきますね。
とりあえず、この\(y=x^2\)を表にしていこう。
\(x\)を\(-4\)〜\(4\)までを表にしていくと。。

表にしてみると、わかると思うんだけど、この「関数 \(y=ax^2\)」では
\(y\)の値っていうのは、\(x\)の値がどうであっても、正の数になっているんだね。
ちなみに、この\(y\)の値が正の数になっているっていうのは、比例定数の\(a\)の値によって
変わってくるのでそこは注意しておこう。
(このあとに、比例定数\(a\)によるグラフの違いの解説を行いますね。)
次に\(y=x^2\)の表をもとにグラフを書いていきますね。
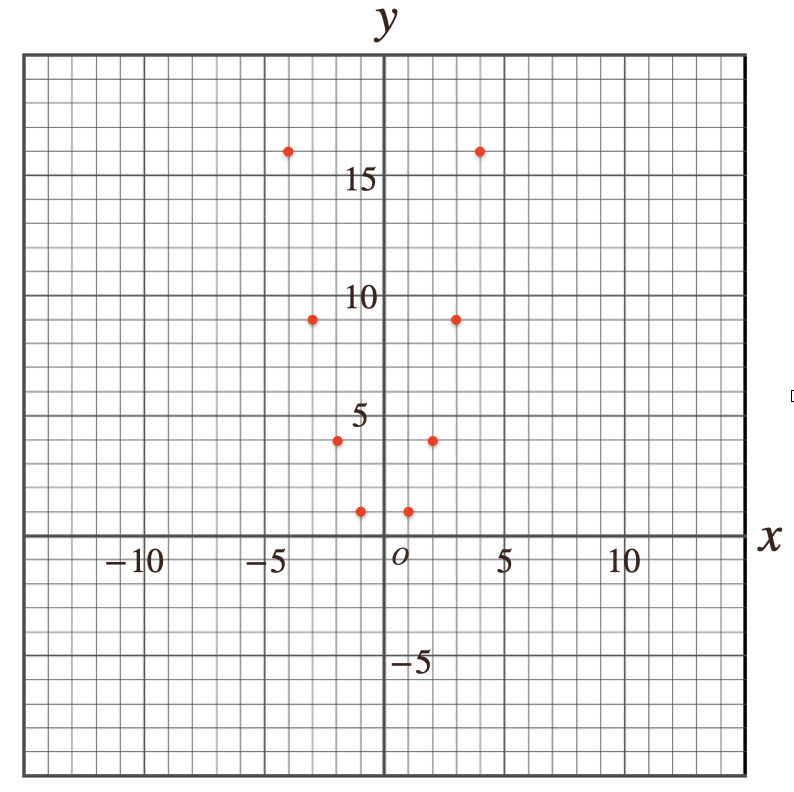
まずは、表をもとに各座標に点をうって、あとはこれを線でつなげてグラフを
完成させると。。
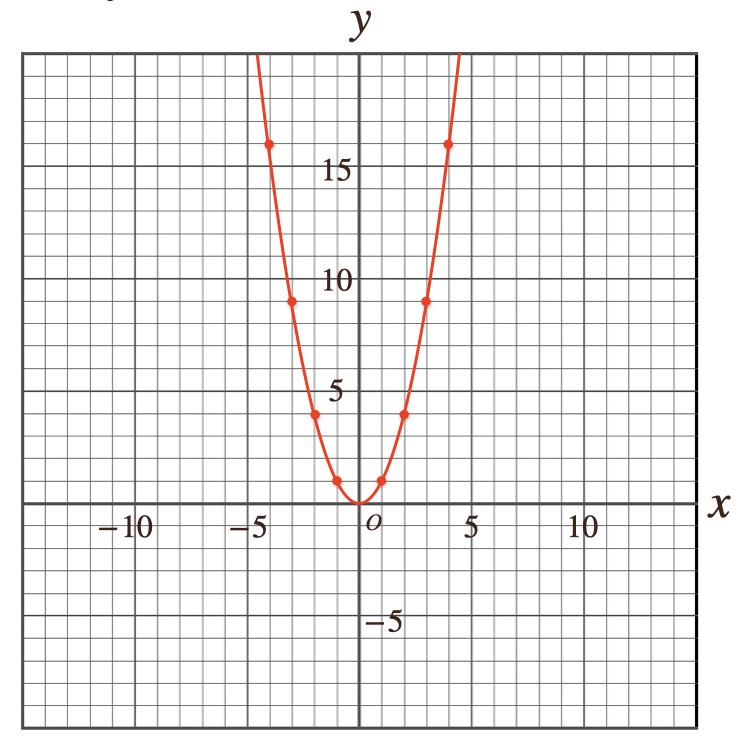
これが、\(y=x^2\)のグラフになりますね。
中学1年生で習った、関数とはまた違ったグラフになるんですね。
特徴としては、関数\(y=ax^2\)のグラフは曲線になっていて
これを放物線(ほうぶつせん)って言うんだね。それと、\(y\)軸を中心に左右対称に
なっているんだけど、この放物線の対称軸を放物線の軸っていう言い方をするんだね。
今回のグラフは放物線は上向きになっていて、これは\(y\)の値が正の数になっているんだけど
これって言うのは、比例定数の\(a\)の符号によって、向きが変わってくるんですね。
これは、\(y=2x^2\)と\(y=-2x^2\)で表とグラフを書いて比較していくと。。
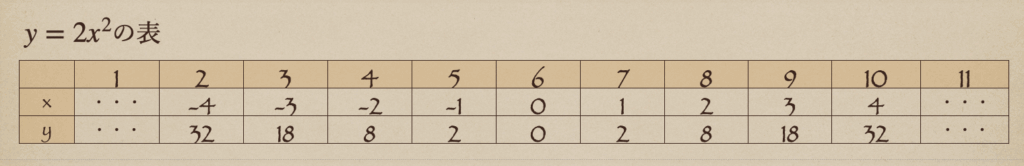
まずは、\(y=2x^2\)の場合は、\(y\)は正の数になっていて

逆に、\(y=-2x^2\)の場合は、\(y\)は負の数になっていてこれをそれぞれグラフに
書き出していきますね。
まずは、\(y=2x^2\)のグラフは。。
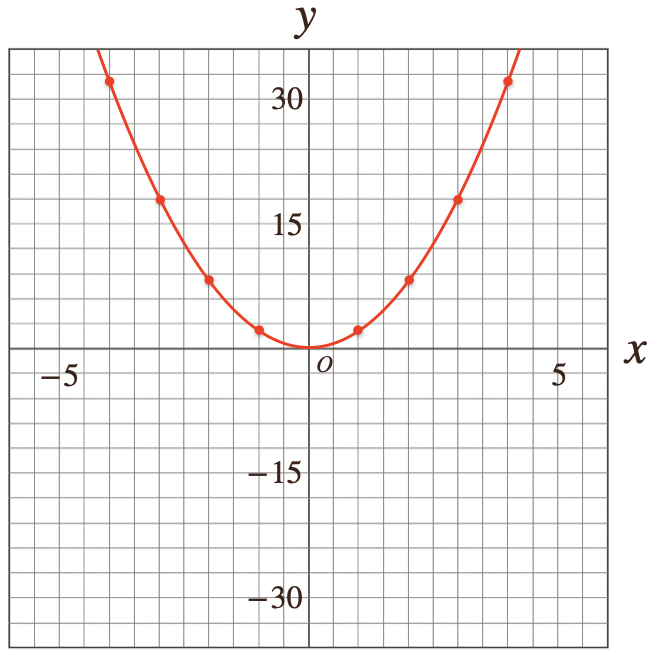
\(y=-2x^2\)のグラフは。。
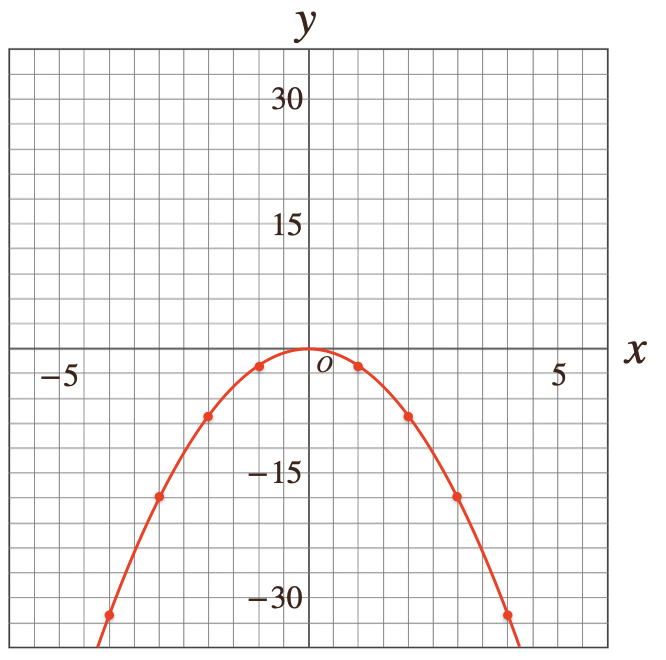
こんな風になって、比例定数\(a\)の符号によって関数\(y=ax^2\)のグラフの向きも
変わってくるってことなんですね。
\(a\)が正の符号の場合:グラフは上向き
\(a\)が負の符号の場合:グラフは下向き
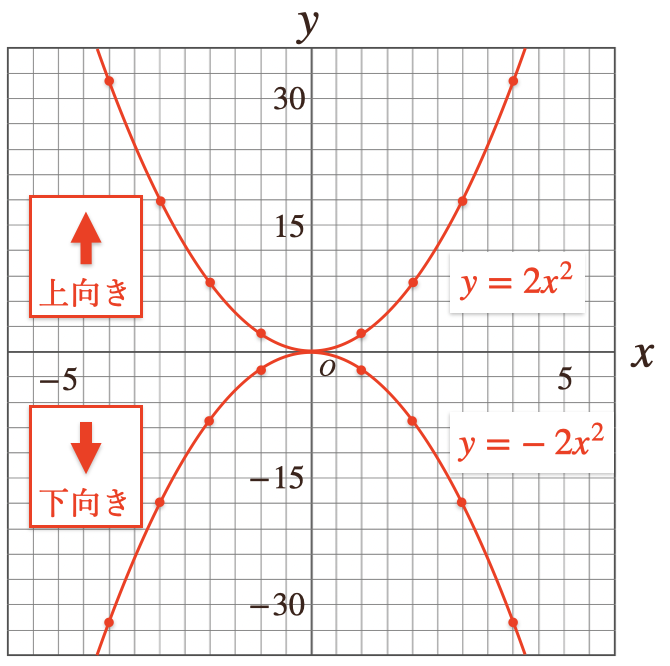
なので、関数\(y=ax^2\)の比例定数\(a\)の符号を見てあげることで
グラフの向きっていうのが、簡単に判断できるってことなんだね。
[3] 関数\(y=ax^2\)の値の変化と変域
次は値の変化ってところを見ていきますね。
これは関数\(y=ax^2\)の\(x\)の値が変化したときに、\(y\)の値がどう変化するのかっていうのを
確認していこう。
関数\(y=ax^2\)の場合、比例定数\(a\)の符号によって変わってくるんだね。
[\(a>0\)のとき]
・\(x<0\)では、\(x\)の値が増加すると対応する\(y\)の値は減少する
・\(x=0\)では、\(y=0\)となり、\(y\)は最小値となる
・\(x>0\)では、\(x\)の値が増加すると対応する\(y\)の値も増加する
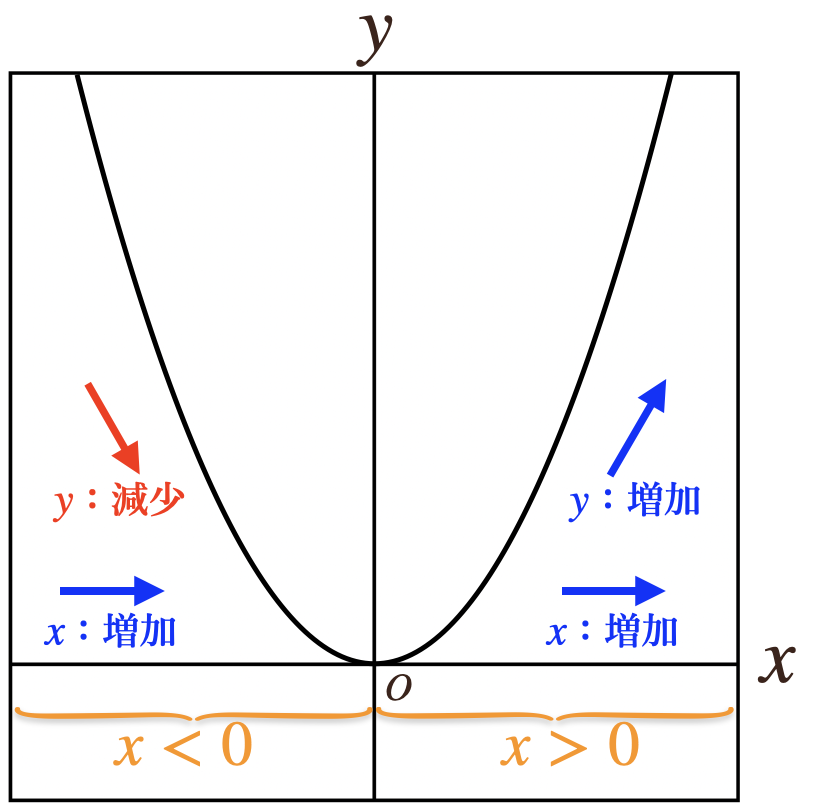
[\(a>0\)のとき]
・\(x<0\)では、\(x\)の値が増加すると対応する\(y\)の値は増加する
・\(x=0\)では、\(y=0\)となり、\(y\)は最大値となる
・\(x>0\)では、\(x\)の値が増加すると対応する\(y\)の値も減少する
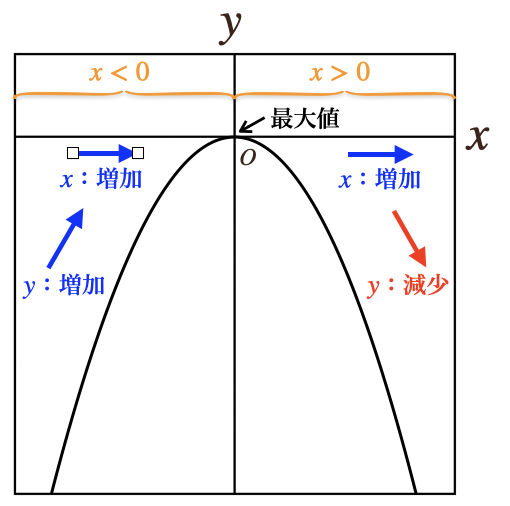
こんな風に、比例定数\(a\)の符号によって、\(x\)の増加によって\(y\)は
増加したり、減少したりするんだね。
次は、関数\(y=ax^2\)の変域についてみていくね。
関数\(y=ax^2\)で\(x\)の変域に対応する\(y\)の変域をグラフにしてみるね。
例)関数\(y=2x^2\)で\(x\)の変域が\(-2≦x≦3\)のときの\(y\)の変域
まずは、\(-2≦x≦3\)から\(x=-2\)と\(x=3\)のときの\(y\)の値を求めてあげると
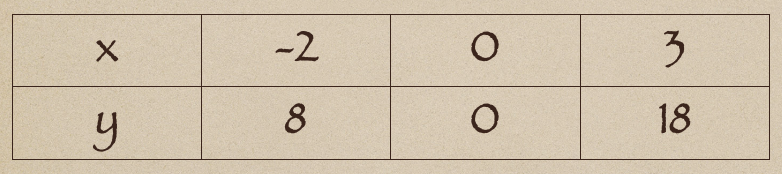
となって、これで\(y\)の変域は\(8≦y≦18\)と答えてしまいそうになるんだけど
この、関数\(y=2x^2\)の変域は一次関数と少し違っていて、関数\(y=2x^2\)をグラフに書くと
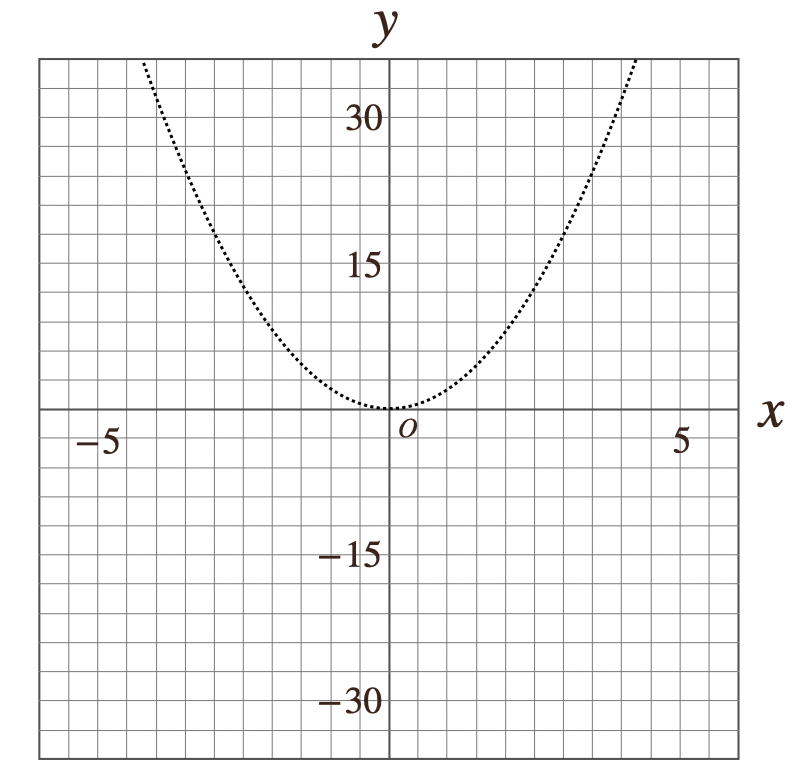
となるんだけど、今回のグラフは変域があるのでグラフはまだ、点線で書いているんだけど、ここに、変域の値をグラフに書き込むと。。
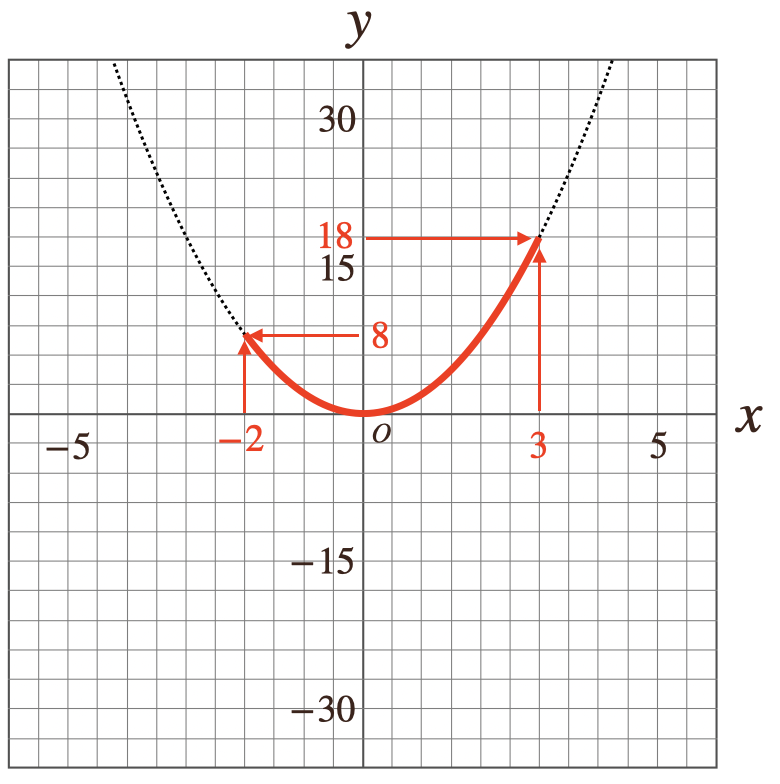
ここから\(y\)の変域を見ていくと、最小値っていうのは、\(8\)ではなくて
グラフから、\(0\)であることがわかるよね。そして、最大値はっていうと
\(x=3\)のときの\(y\)の値ってことになるので、\(18\)となって
\(y\)の変域は\(0≦y≦18\)ってことになりますね。なので
関数\(y=ax^2\)の\(y\)の変域は、\(x\)の変域が\(y\)軸をまたいでいるとき
\(a>0\)のとき、\(y=0\)が最小値となり
\(a<0\)のとき、\(y=0\)が最大値となる
こう言った特徴があるので、変域をもとめるさいには、注意が必要だね。
[4] 関数\(y=ax^2\)の変化の割合
一次関数\(y=ax+b\)の場合の変化の割合を思い出してみよう。
例えば、1次関数 \(y=2x-3\)で\(x\)が\(-2\)から\(2\)に移動したときの
変化の割合は\(2\)となって
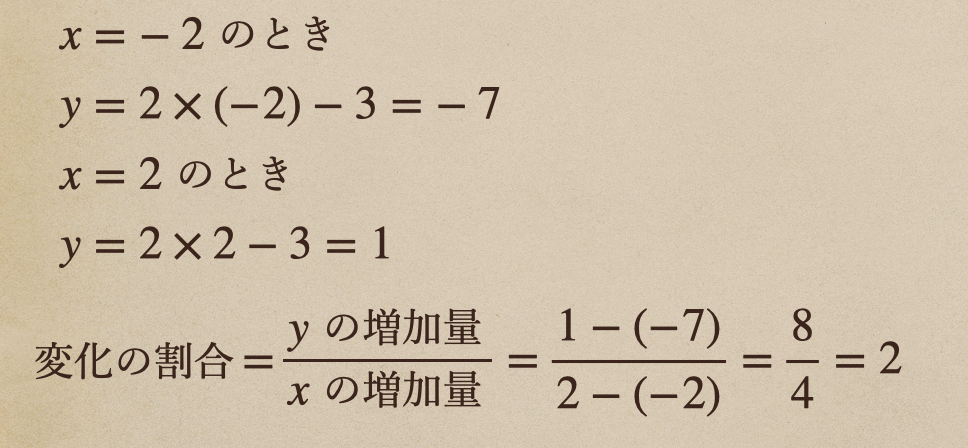
これは、比例定数と同じになるんだね。
ようするに、一次関数の場合は、\(x\)の増加量がいくつであっても
\(y=2x-3\)の変化の割合\(2\)になるってことなんだね。
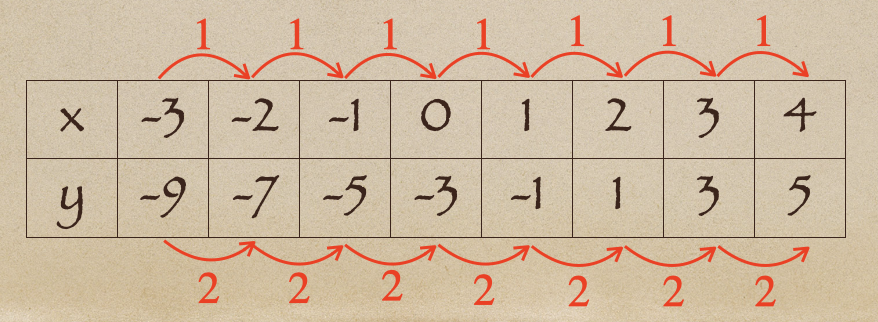
これが一次関数ってことでしたよね。
それじゃあ、関数\(y=ax^2\)の場合、どうなるかを見て行ってみよう。
例は\(y=2x^2\)として、表を作ってみて\(x\)の増加量と\(y\)の増加量を確認して行ってみるね。
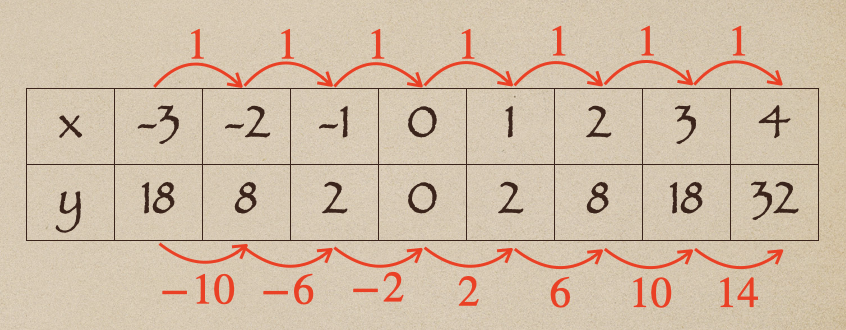
関数\(y=ax^2\)の場合は、このようになって、これっていうのが
関数\(y=ax^2\)は、変化の割合は一定ではない
ってことになるんだね。
[5] 関数\(y=ax^2\)の式の求め方
この関数\(y=ax^2\)の式を求めようと思うと、比例定数の\(a\)の値を
求められたら、いいってことになりますね。
例) \(y\)は\(x\)の2乗に比例して、\(x=-2\)のとき\(y=12\)である。
このとき、\(y\)を\(x\)の式で表しなさい。
ここで、『\(y\)は\(x\)の2乗に比例』するってことなので、この関数は
\(y=ax^2\)ってことが言えるんだね。そして『\(x=-2\)のとき\(y=12\)』って
ことなので、\(y=ax^2\)に\(x=-2\)と\(y=12\)を代入してあげて
\(12=a×(-2)^2\)
\(12=4a\)
\(a=3\)
となるので、この例題の答えは、「\(y=3x^2\)」ってことになりますね。
グラフから式をもとめる場合は次のことが言えるんだね。
頂点を原点とする放物線の式は、\(y=ax^2\)で表されるため
\(a\)の値を求めれば式を求めることができる
関数\(y=ax^2\)の式を求めるのは、\(x\)と\(y\)の値がわからないと\(a\)の値を
求めることがむずかしいんだけど、逆に、\(x\)と\(y\)の値がわかってしまえば
簡単に\(a\)の値を求めることはできるんだね。
今回は、ここまでになります。
ここまでの記事が良かったと思ったらここをクリックしてね。
質問なんかがあった場合はコメントにお願いします。
では、また、さようなら。


.jpeg)
コメント