どうも、こんにちはDKです。
今回は、中学3年生の相似な図形で「図形の比」について
やっていきますね。
前のブログで相似な図形の基礎についての解説しているので
相似っていうのがどういったものかっていうのを学んでから
こっちの図形の比を見てもらった方が、より理解ができると思うので
よかったら、相似に関する知識をしっかりと身につけて行ってもらえれば
いいかなと思います。
(1) 三角形の比
三角形の比っていうのは
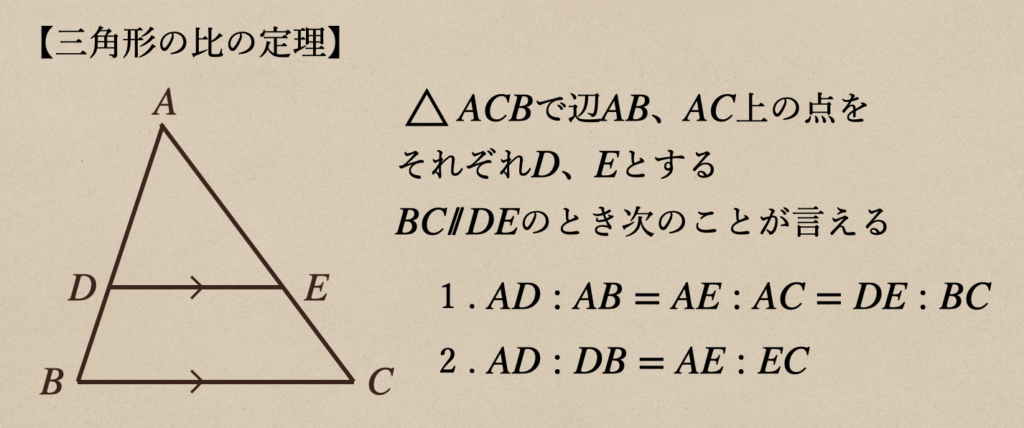
この定理がなぜ言えるのかっていうのをここでは確認しつつ
三角形の比の定理について理解を深めていこう。
三角形の比の定理が言えるようにするにはそうであることを証明してあげればいいよね。
なので、次のことを証明してみよう。
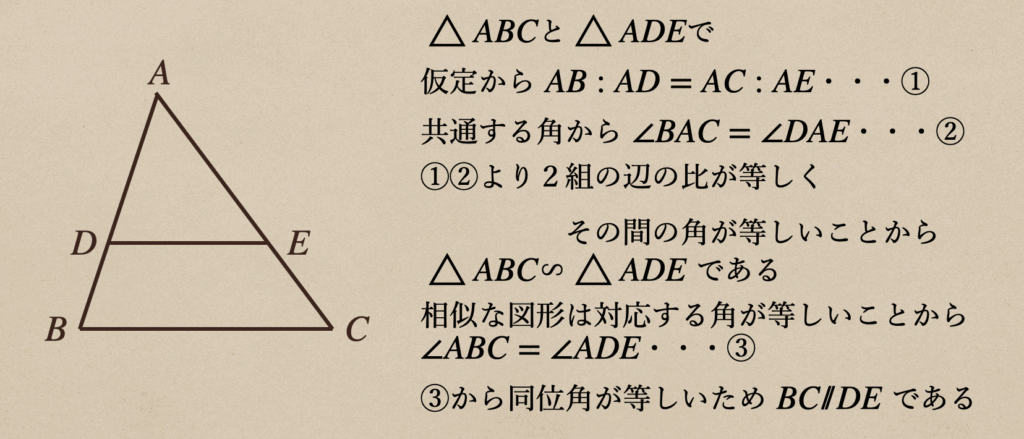
\(\triangle{ABC}\)で辺\(AB\)、\(AC\)上に\(BC/\!/DE\)となる点\(D\)、\(E\)をとる
このとき、\(\triangle{ABC}\)と\(\triangle{ADE}\)であることを証明する
まずここから、仮定と結論を確認しておこう。
仮定:\(BC/\!/DE\)
結論:\(\triangle{ABC}\)∽\(\triangle{ADE}\)
これを踏まえて、証明すると。。。
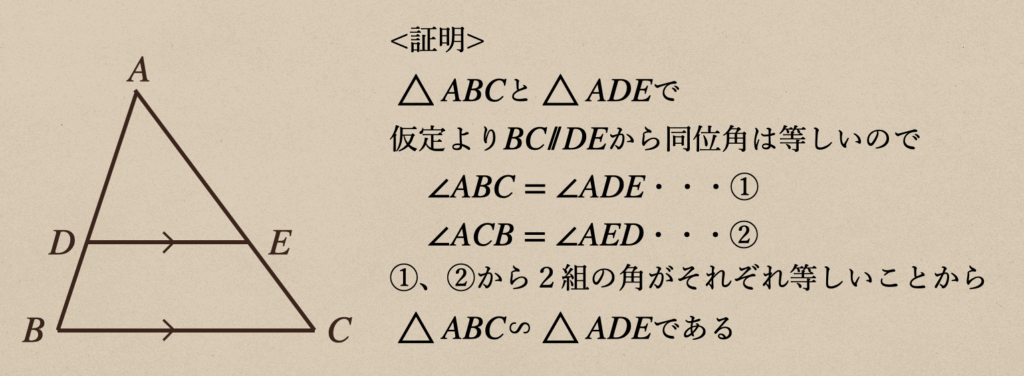
これで、\(\triangle{ABC}\)∽\(\triangle{ADE}\)が証明できて
相似であるってことは「3組の辺の比はそれぞれ等しい」ってことも言えるので
\(AB:AD=BC:DE=AC:AE\)ですよってことになりますね。
これで、三角形の比の定理の一つ目が証明できましたね。
次にもう一つの定理である\(AD:DB=AE:EC\)であることを証明していこう。
\(\triangle{ABC}\)で\(BC/\!/DE\)ならば、\(AD:DB=AE:EC\)であることを証明する
これを証明するにはまず、点\(D\)から\(BC\)上に\(DF/\!/AC\)となる点\(F\)を
おいてあげてから証明をしていけば。。。
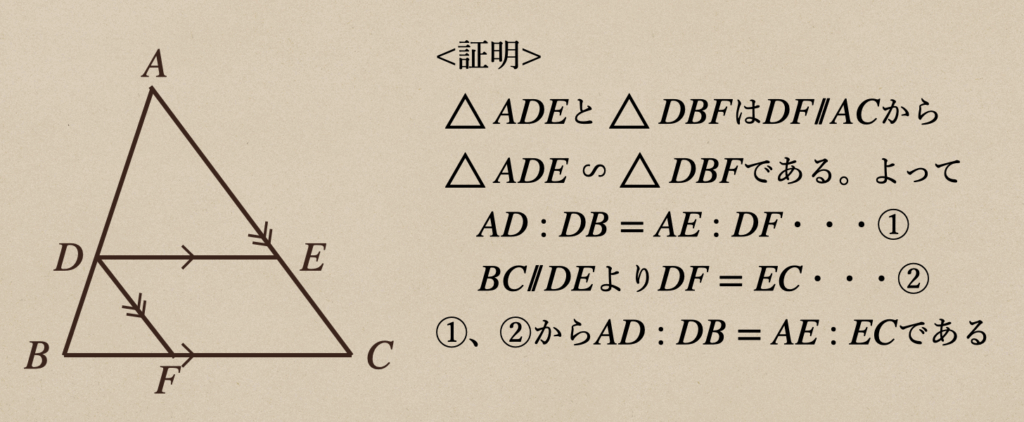
これで、証明ができたってことなので2つ目の三角形の比の定理が証明できたことになりますね。
次にこの三角形の比の定理っていうのが逆の場合でも証明できるのかっていうのを
見ていきますね。
(2) 三角形の比の定理の逆
三角形の比の定理っていうのは、三角形の中に三角形の辺と平行な線が引かれた場合
辺の比が等しくなりますよってことだったので、その逆はって言うと辺の比が等しかったら
三角形の中に引かれた線分っていうのは、三角形の辺と平行になりますよってことなんですね。
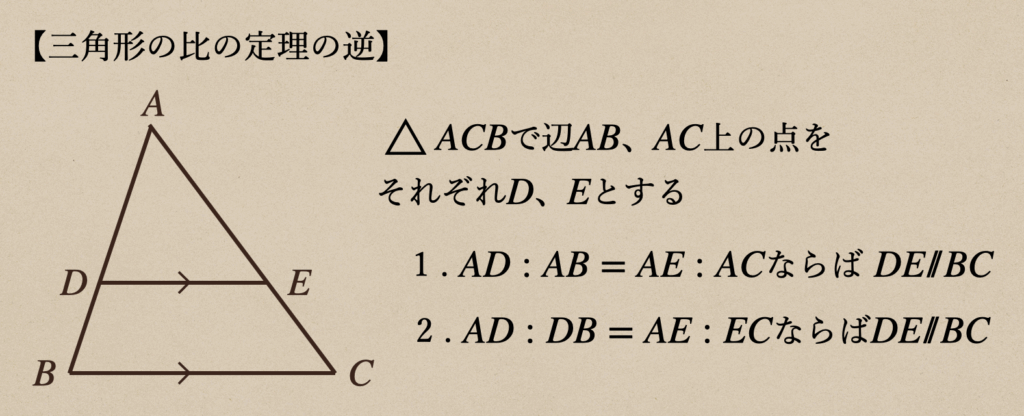
これが成り立っているのかっていうのを証明して確認していこう。まずは
\(\triangle{ABC}\)で辺\(AB\)、\(AC\)上に\(AD:AB=AE:AC\)となる
点\(D\)、\(E\)をとる。このとき、\(DE/\!/BC\)であることを証明する
証明になるので、まずは仮定と結論を確認しておきますね。
[仮定] \(AD:AB=AE:AC\)
[結論] \(DE/\!/BC\)
ですね。これから証明していくと。。
これで、一つ目の証明ができましたね。次は。。
\(\triangle{ABC}\)で辺\(AB\)、\(AC\)上に\(AD:DB=AE:EC\)となる
点\(D\)、\(E\)をとる。このとき、\(DE/\!/BC\)であることを証明する
ここも、仮定と結論を確認しておきますね。
[仮定] \(AD:DB=AE:EC\)
[結論] \(DE/\!/BC\)
この証明では、点\(B\)から\(AE\)と平行となるように\(DE\)の延長線との交点を
\(F\)として、そこから\(\triangle{ADE}\)と\(\triangle{BDF}\)は相似であるので
この相似を使って\(DE/\!/BC\)を証明していきましょう。

これで、2つ目の証明もできたので、ここから、三角形の比の定理の逆が
証明されたってことですね。
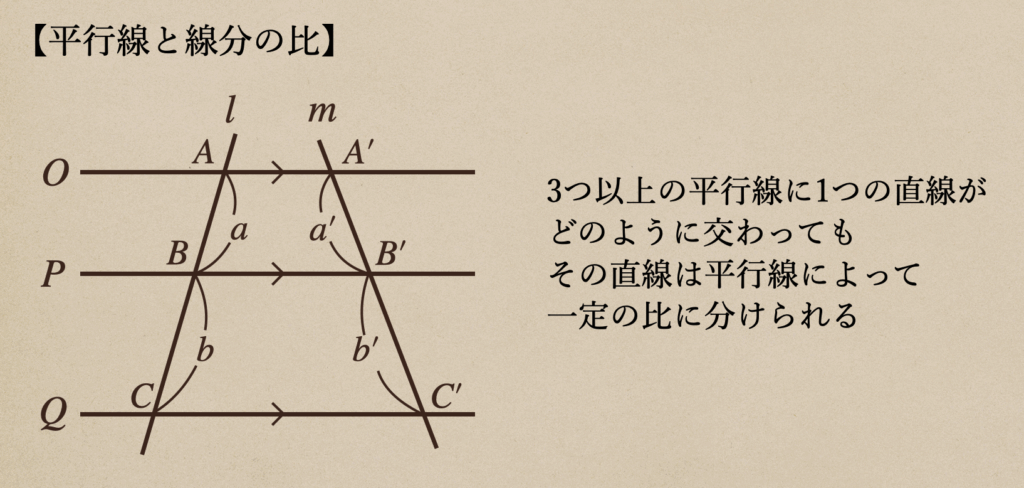
(3) 平行線と線分の比
ここまでの、三角形の比の定理が言えることで、平行に引かれた直線に交わる
線分の比の関係っていうのも、次のことが言えるってんですね。
ここでも、なんでこの「平行線と線分の比」が成り立っているのかっていうのを
平行な3直線\(O\)、\(P\)、\(Q\)に2直線\(l\)、\(m\)が交わっているとき
\(AB:BC=A’B’:B’C’\) であることを証明する
これを証明するには、直線\(O\)で直線\(l\)と\(m\)を交差させると
三角形ができるんですね。そこから、証明していけばいいですね。
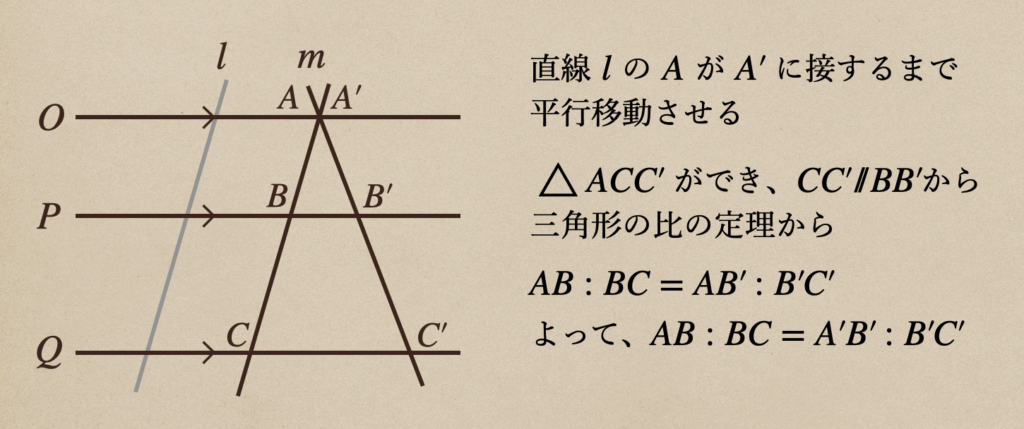
こうやって、三角形の比の定理を応用することで、平行線と線分の比も定理することが
できるんですね。
次も三角形の比の定理の応用になりますね。
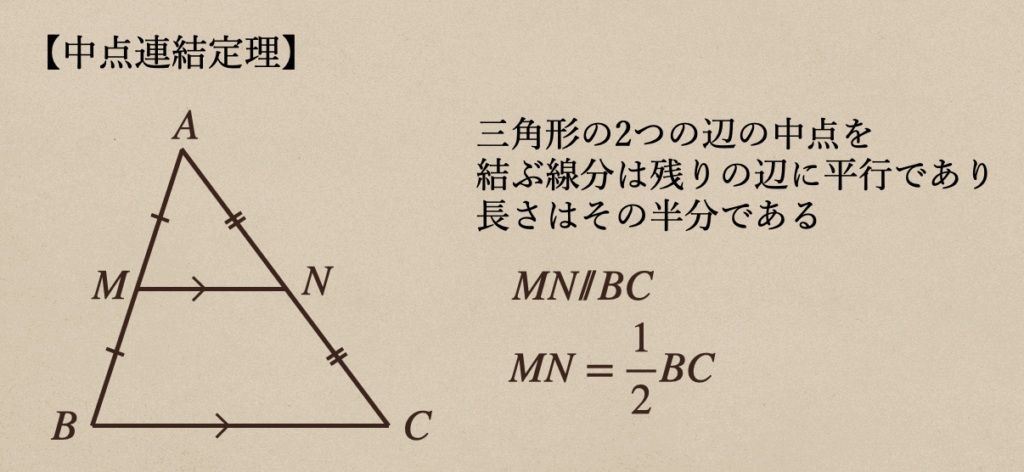
(4) 中点連結定理
これは、三角形の2つの辺の中点に引かれた線分の関係を定理として言っているんだね。
それが、どう言ったものかっていうと。。
これも、証明して、本当にそうなっているのかを確認してみよう。
\(\triangle{ABC}\)の辺\(AB\)と\(AC\)の中点を\(M\)、\(N\)とすると
\(MN/\!/BC\)、\(MN=\frac{1}{2}BC\)であることを証明する
これの証明は、三角形の比であることを証明して行ってあげればいいってことになりますね。
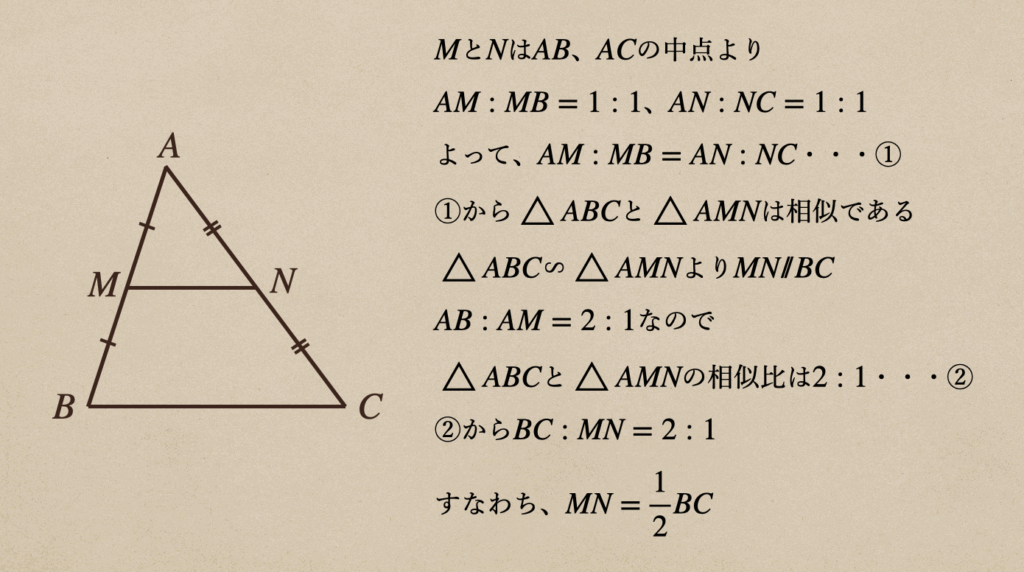
これのポイントは三角形の2つの辺の中点を結ぶと残りの辺と平行になりますよってことですね。
ここまでが、三角形の比の定理を活用した相似な図形の比の関係になりますね。
次は相似であることを証明することで、三角形を二分する辺の比について
解説していきますね。
(5) 三角形の角の二等分線の比
これは、三角形の角の二等分線を引いたときに次のことが言えるってことなんですね。
これも証明することで、この定理がちゃんと成り立っているってことが
わかるんですね。
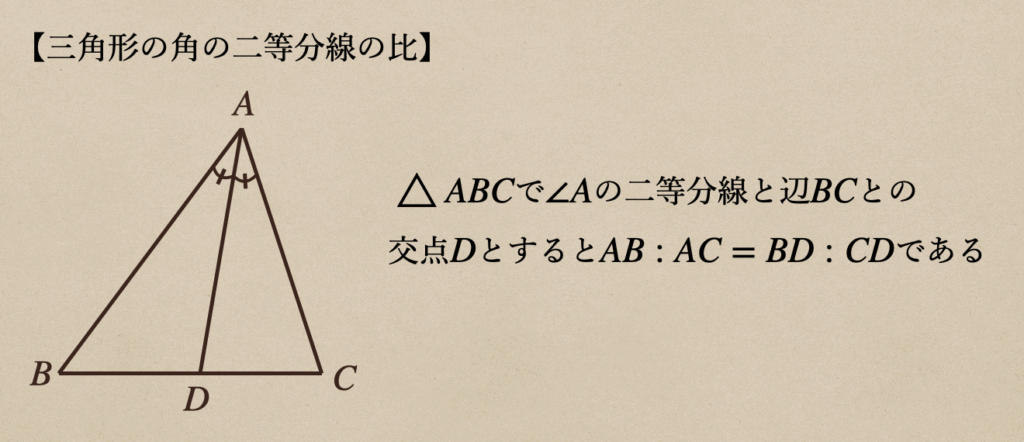
\(\triangle{ABC}\)で\(\angle{A}\)の二等分線を辺|\(BC\)の
交点を\(D\)とするとき、\(AB:AC=BD:CD\)であることを証明する
これも、相似であることを証明して、三角形の比の定理を利用していけば
証明することができるんですね。
証明するために、少し補助線を引いて行きますね。
点\(C\)から\(AD\)に平行な直線と\(BA\)を延長した直線の交点を\(E\)と
して見て行きますね。
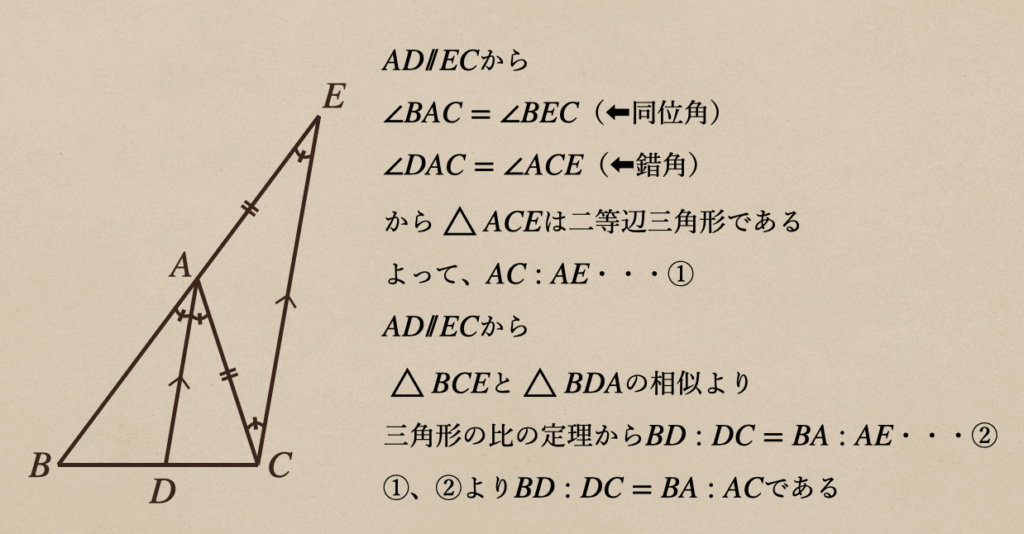
これで、二等分線の引かれた線分の比に定理が当てはまることが証明できましたね。
この定理も、よく利用されて問題が出題されるので、しっかり覚えていってくださいね。
(6) 平行線と図形の面積
平行に引かれた直線の中にある、図形の面積について考えて行きましょう。
\(AD/\!/BC\)、\(AD:BC=1:2\)の台形\(ABCD\)があり
対角線の交点を\(O\)とする。
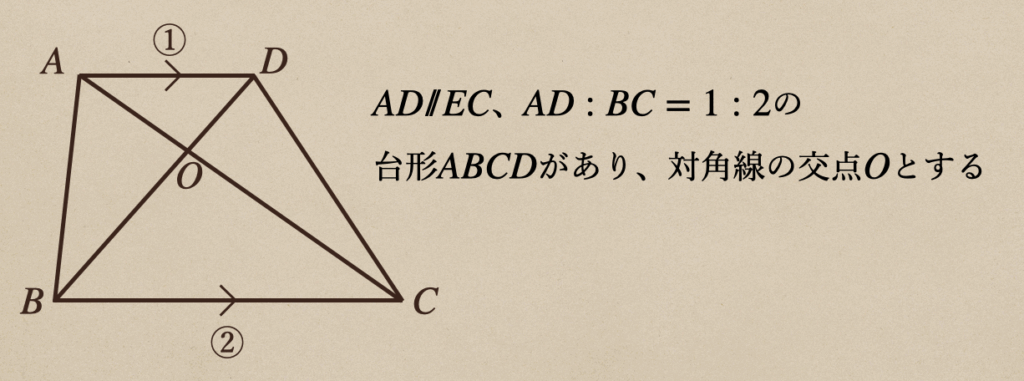
このとき三角形どうしの面積の比について考えてみよう。
ここで、まず注目するのは辺\(AD\)と\(BC\)は平行ってことなので
どこをとっても高さっていうのは同じになりますよね。
ようするに、三角形の面積は底辺によって決まってきますよってことになるんだね。
例えば\(\triangle{ABD}\)と\(\triangle{ACD}\)は底辺が同じ辺\(AD\)ってことなので
面積は\(\triangle{ABD}=triangle{ACD}\)となるんですね。
\(AD:BC=1:2\)ってことなので面積も辺の比と同じになって
\(\(\triangle{ABD}:triangle{BCD}=AD:BC=1:2\)になるってことですね。
平行に引かれた線上に頂点を持つ三角形で、底辺が同じであれば面積は等しく
底辺の比が面積の比になるってことになるんですね。
今回は、ここまでになります。
ここまでの記事が良かったと思ったらここをクリックしてね。
質問なんかがあった場合はコメントにお願いします。
では、また、さようなら。



コメント