どうも、こんにちはDKです。
今回は、中学3年生の相似な図形の「相似な図形の体積」について
やって行きますね。
中3-5(2)で「図形の比」についてやってきたんですけど、その最後に
平行線と図形の面積っていうのを解説したんですけど、ここで解説する
相似な図形の体積や面積っていうのと混同してしまうこともあるので
しっかり違いを理解して使い分けができるようにして行ってくださいね。
中3-5(1)では「相似な図形の基礎」についても解説しているので
よかったら、そっちも見てみてください。
(1) 相似な図形の面積
相似な図形には相似比っていうのがあったかと思うんだけど
相似比っていうのは辺の長さの比を表していて、これっていうのは
面積の比って言うわけではないんですね。
じゃあ、相似比に対して、面積比って言うのがどうなっているのかっていうのを
確認してみよう。
ここでは相似比が\(1:3\)の相似な図形の面積を見ていこう。
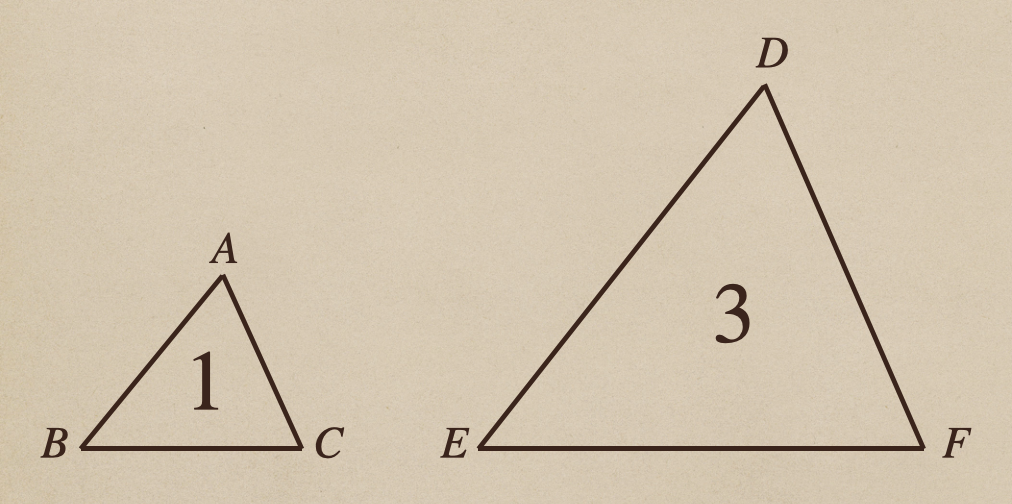
\(\triangle{ABC}:\triangle{DEF}=1:3\)の相似な図形があったとして
これらの面積を求めていくのに\(\triangle{ABC}\)の底辺を\(a\)として
高さを\(h\)とした場合、\(\triangle{DEF}\)の底辺は\(3a\)となって
高さは\(3h\)となるってことですね。
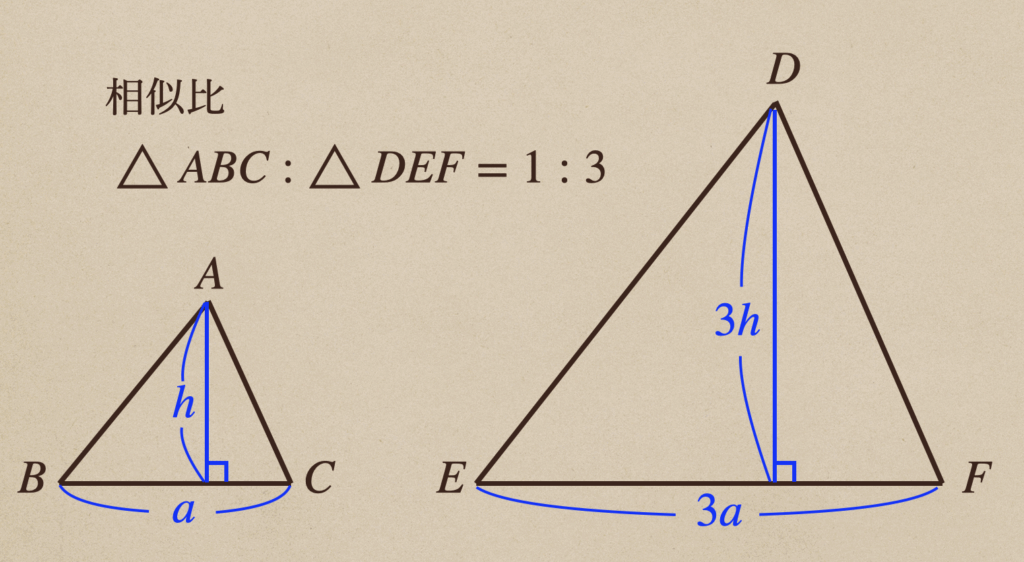
ここからそれぞれの面積を計算すると
\(\triangle{ABC}=\frac{1}{2}×a×h=\frac{1}{2}ah\)
\(\triangle{DEF}=\frac{1}{2}×3a×3h=\frac{9}{2}ah\)
となりますね。これから\(\triangle{ABC}:\triangle{DEF}\)の面積の比は
\(\frac{1}{2}ah:\frac{9}{2}ah=1:9\)になるってことですね。
相似比\(1:3\)に対して、面積比\(1:9\)ってことから面積比っていうのは
相似比の2乗されていることになりますね。
ようするに、こう言うことになるんだね。
<相似な図形の面積の比>
相似比が\(a:b\)である2つの図形の面積比は\(a^2:b^2\)となる
これが相似比と面積比の関係になるってことなんですね。
これをふまえて、今度は相似な立体の表面積比について考えてみよう。
(2) 相似な立体の表面積
今度は、相似な立体について見て行きますね。
立体なので、わかりやすいように相似な立方体で見て行きましょう。
相似比はさっきと同じ\(1:3\)で表面積の比の関係がどうなるのかを見て行きますね。
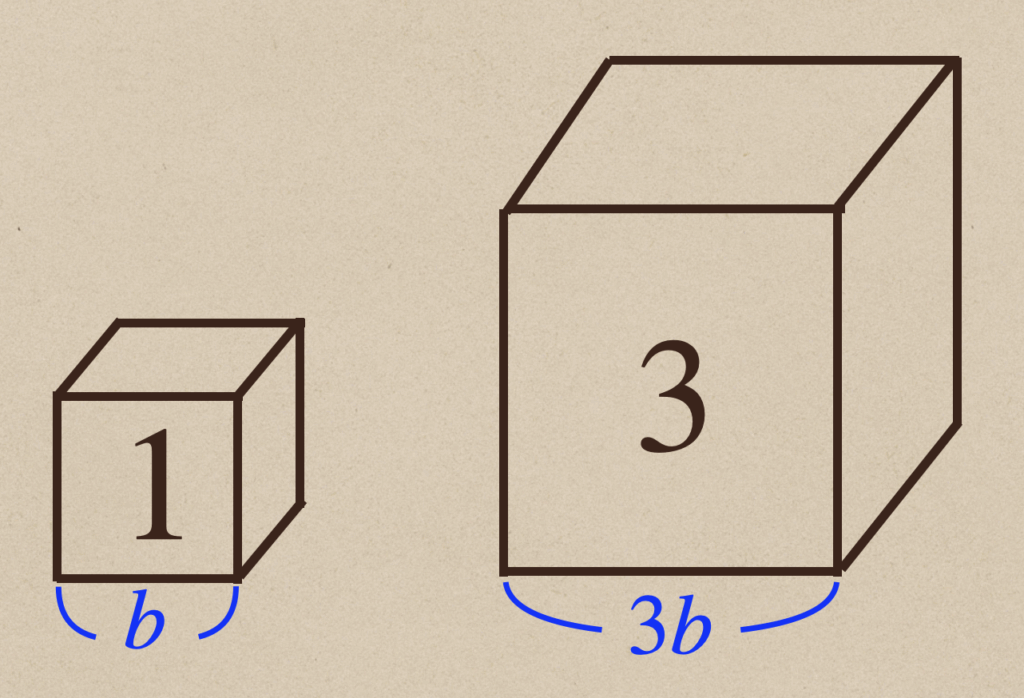
小さい方の立体の1辺を\(b\)とすると大きい方の1辺は\(3b\)となりますね。
立方体なので、すべての辺が同じになるってことですよね。
ここから、それぞれの表面積を計算してあげると
小の立方体:\((b×b)×6=6b^2\)
大の立方体:\((3b×3b)×6=54b^2\)
で、表面積の比は\(6b^2:54b^2=1:9\)となるので、これも相似な図形の面積と
同じで\(1:3^2\)となるってことですね。ようするに
<相似な立体の表面積の比>
相似比が\(a:b\)である2つの立体の表面積の比は\(a^2:b^2\)となる
ってことなんですね。
相似な立体の表面積の比は相似な図形の面積の比と同じ相似比を
2乗してあげればいいってことになりますね。
(3) 相似な立体の体積
最後は、相似な立体の体積について見て行きますね。
ここまで来れば、なんとなく定理も予想がついてしまうかもしれないんだけど
本当にそうなのかって言うのをここでは、確認していくことにしますね。
ここでも、相似比は\(1:3\)で見て行きますね。
今回は、長方体で小さい方のタテ、ヨコ、高さが\(a\)、\(b\)、\(c\)として
見て行きますね。
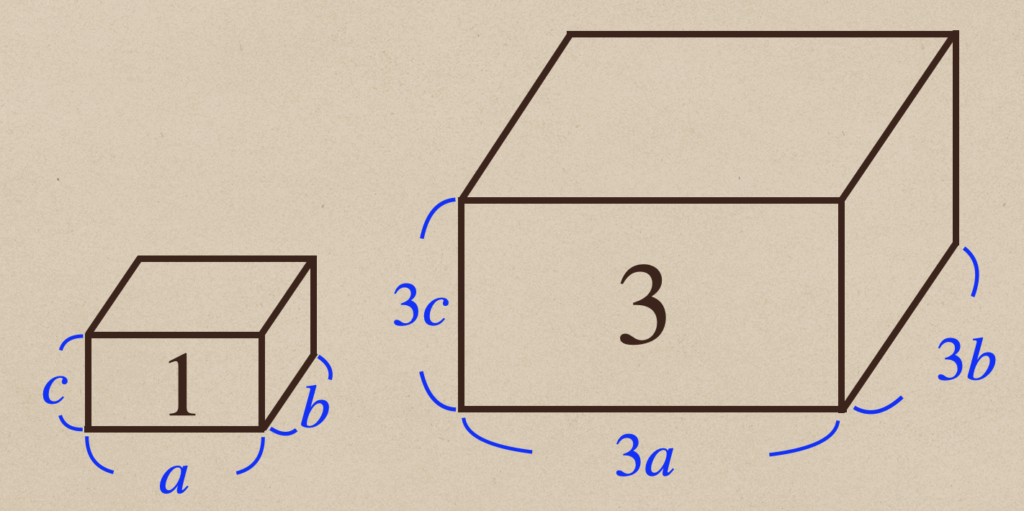
ここから、それぞれの直方体の体積を計算してみると
小の直方体:\(a×b×c=abc\)
大の直方体:\(3b×3b×3c=27abc\)
となって、体積の比は\(abc:27abc=1:27\)となるんですね。
このことから、相似な立体の体積は次のことが言えるってことになるんだね。
<相似な立体の体積の比>
相似比が\(a:b\)である2つの立体の体積の比は\(a^3:b^3\)となる
これで、相似な図形/立体の面積、表面積、体積の求め方がわかってもらえたかな?
2乗するのか3乗するのかっていうのは、面積と体積の単位っていうのを考えてあげれば
簡単に判断できてくるよ。
面積の単位:\(mm^2\)(平方ミリメートル)、\(cm^2\)(平方センチメートル)
体積の単位:\(mm^3\)(立方ミリメートル)、\(cm^3\)(立方センチメートル)
面積の場合、単位には2乗がついていて、体積の場合は単位に3乗がついているよね
これを見てあげれば、相似比に2乗するのか、3乗するのかっていうのがわかるよね。
今回は、ここまでになります。
ここまでの記事が良かったと思ったらここをクリックしてね。
質問なんかがあった場合はコメントにお願いします。
では、また、さようなら。



コメント