どうも、こんにちはDKです。
今回は中学3年性の「三平方の定理」について解説を行っていきますね。
前の項では三平方の定理の基礎の部分で、今回はタイトルにもあるように
「図形の計量」や[座標平面]の辺や体積を求めていく方法について
解説行っていきますね。
1.平面図形の計量
三平方の定理が使えると直角三角形の2辺が分かればもう1つの辺もわかるってことなので
これを使って、平面図形で長さを求めて行ってみよう。
まずはこれからだね。
・正方形の対角線の長さを求める
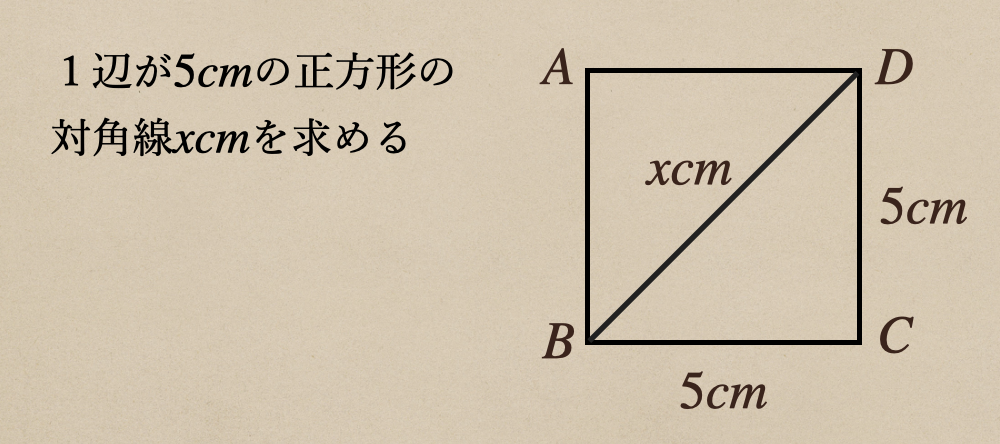
正方形の内角は\(90^\circ\)なので\(\triangle{BCD}\)は直角三角形って
ことになるよね。なので、三平方の定理が使えて\(BD^2=BC^2+CD^2\)となるね。
\(BC=CD=5\)で、対角線\(BD\)は\(xcm\)を代入してあげて
\(x^2=5^2+5^2\)
\(x^2=25+25=50\)
\(x=\sqrt{50}\) \(x>0\)
\(x=5\sqrt{2}\) //
今までは、四角形の対角線を求めることがむずかしかったけど、三平方の定理を
使えば簡単に求めることができるんだね。
・三角形の面積を求める
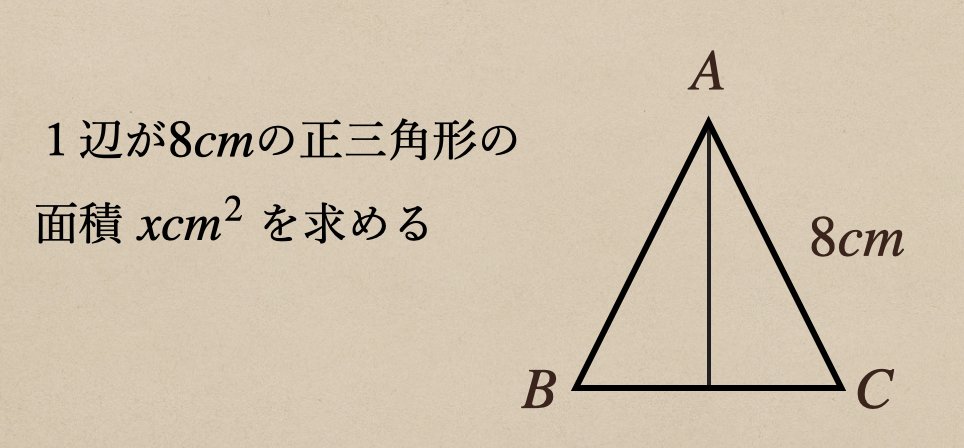
面積を求めるってことなので、三角形の高さを求めることができれば
底辺×高さ÷\(\frac{1}{2}\)で面積を求めることができるね。
頂点\(A\)がら\(BC\)に垂直に接する点を\(H\)としてその長さを\(h\)すると
\(\triangle{AHC}\)は\(HC=4\)、\(AC=8\)、\(AH=h\)の直角三角形と
なるので、ここから高さ\(h\)を求めてあげて\(\triangle{ABC}\)の面積を求めて
いけるよね。
\(8^2=h^2+4^2\)
\(64=h^2+16\)
\(h^2=48\)
\(h=\sqrt{48}\) \(H>0\)
\(h=4\sqrt{3}\)
\(\triangle{ABC}\)の面積:\(8×4\sqrt{3}×\frac{1}{2}=16\sqrt{3}cm^2\) //
これで、三角形の面積を求めることもできたね。
ちなみに、直角三角形で特別な形っていうのがあって、その形の場合、3つの辺の比が
決まっているものがあるんだね。それが二等辺三角形と内角が\(30^\circ\)、\(60^\circ\)、\(90^\circ\)の
三角形でそれらの関係っていうのが。。。
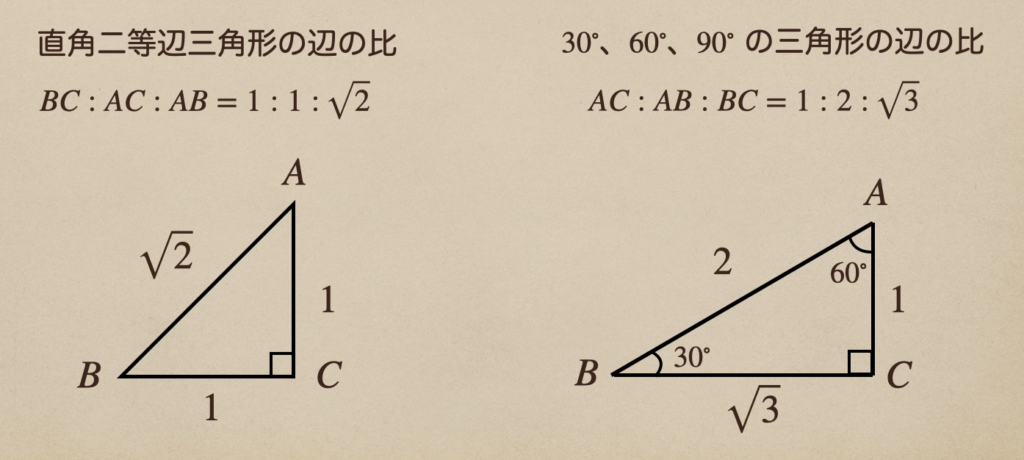
こんな関係があるんだね。これは、どの大きさであっても直角二等辺三角形か
\(30^\circ\)、\(60^\circ\)、\(90^\circ\)の三角形であれば成り立つものになるので
覚えておけば、三平方の定理の式で計算する必要なく、辺を求めることができるよ。
・円と三平方の定理
次は円にひかれた弦の長さを求めるっていうのをやっていこう。
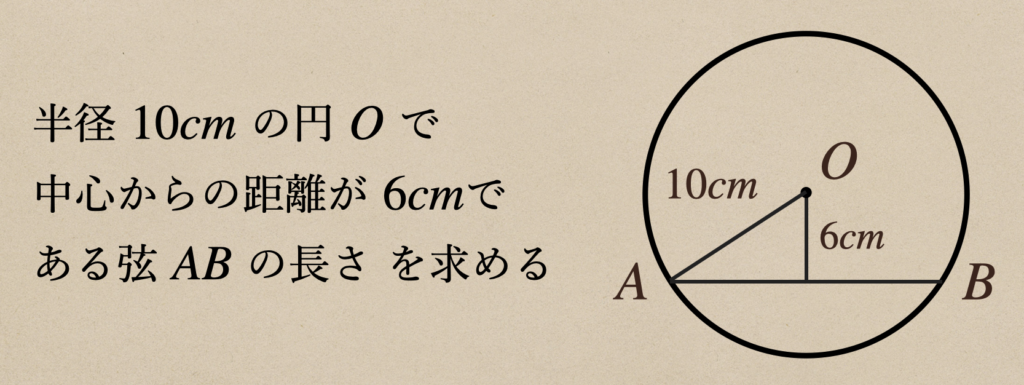
円\(O\)の半径、中心から弦までの距離がわかっていれば、ここから三平方の定理を
求めることができますよね。
中心\(O\)から弦\(AB\)に垂直に引いた点を\(H\)として、\(\triangle{AHO}\)が
直角三角形になっているので、\(AO=10\)、\(OH=6\)、\(AH=x\)としてあげて
\(x\)を求めてあげれば弦\(AB\)も求めていくことができますよね。
\(AO^2=OH^2+AH^2\)
\(10^2=6^2+x^2\)
\(100=36+x^2\)
\(x^2=64\)
\(x=8\) \(x>0\)
\(AB=2AH\)より\(AB=2×8\)//
こういったところでも、三平方の定理は使っていくことができるんだね。
・接線の長さを求める
円の弦を求めたのと同じように円に接する線の長さも求めていくことができるんだね。

\(PA\)は接線ってことなので、\(\angle{OAP}\)は\(90^\circ\)ってことなので
\(\triangle{OAP}\)は直角三角形ってことになるね。
\(OP=12\)、\(AO=8\)、\(PA=x\)ってことなので三平方の定理を使って
\(x\)を求めていけば\(PA\)の長さがわかるよね。
\(OP^2=AO^2+PA^2\)
\(12^2=8^2+x^2\)
\(144=64+x^2\)
\(x^2=80\)
\(x=\sqrt{80}\) \(x>0\)
\(x=4\sqrt{5}\)//
こんな風に直角三角形がある図形であれば2つの辺さえわかれば
もう一つの辺を求めることができるんだね。
2.座標平面上の点と距離
今度は、座標平面上の点の位置からできる図形について見ていきますね。
・座標平面上の2点間の距離
まずは、この図を見てみて
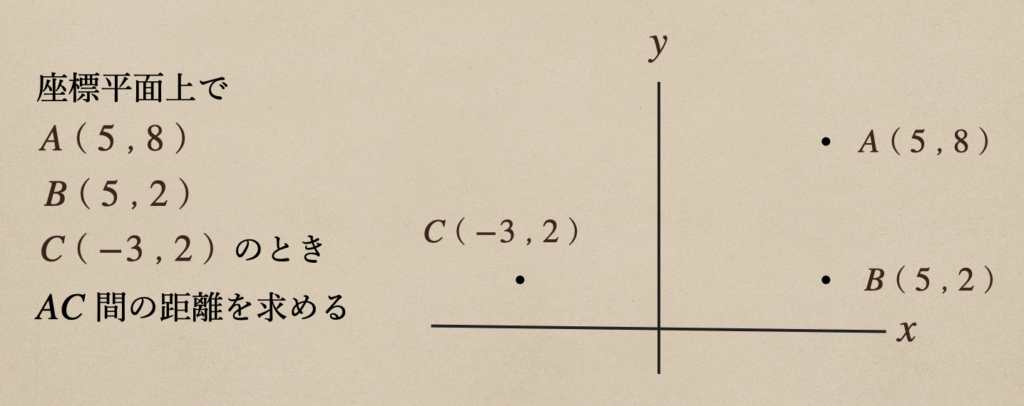
座標平面上の点で、点\(A\)と\(B\)の\(x\)が同じになっていて点\(B\)と\(C\)の\(y\)が
同じになっているってことなので、線分\(AB\)と線分\(BC\)は垂直になっているってこと
なるよね。ようするに、\(\triangle{ABC}\)は直角三角形ってことになるんだね。
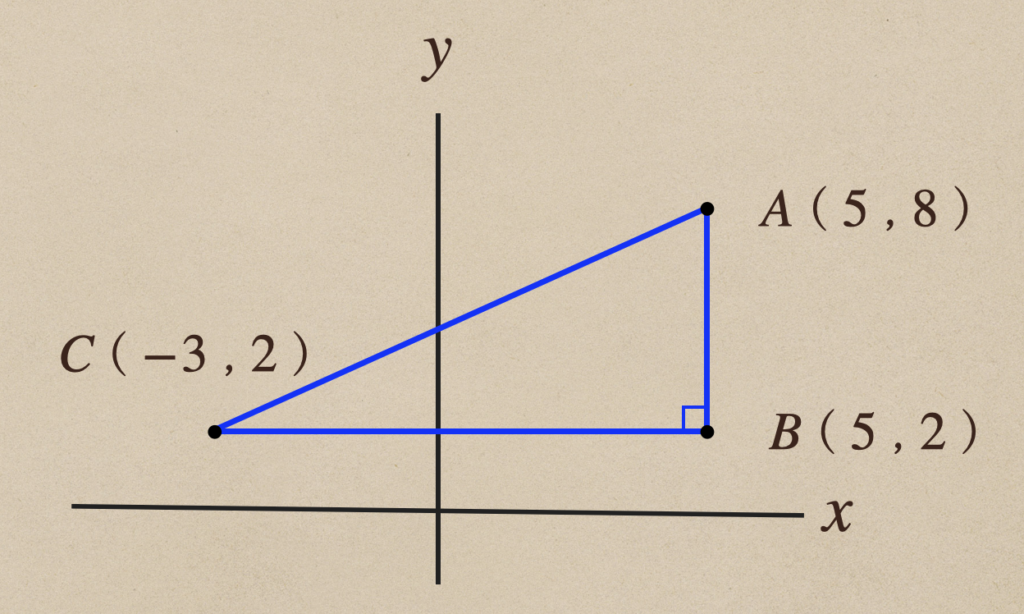
これで、点\(A\)、\(B\)、\(C\)の座標からそれぞれの距離を求めてあげて
三平方の定理を使ってあげて\(AC\)の距離を求めてあげればいいんだね。
\(AB\)の距離:\(8-2=6\)
\(BC\)の距離:\(5-(-3)=8\)
\(AC\)の距離:\(x\)
三平方の定理より \(AC^2=AB^2+BC^2\)
\(x^2=6^2+8^2\)
\(x^2=100\)
\(x=10\) \(x>0\)
よって、\(AC=10\)//
・座標から三角形の形を調べる
今度は、座標平面上に置かれた点を結んでできた図形がどういったものに
なっているのかを見ていきますね。
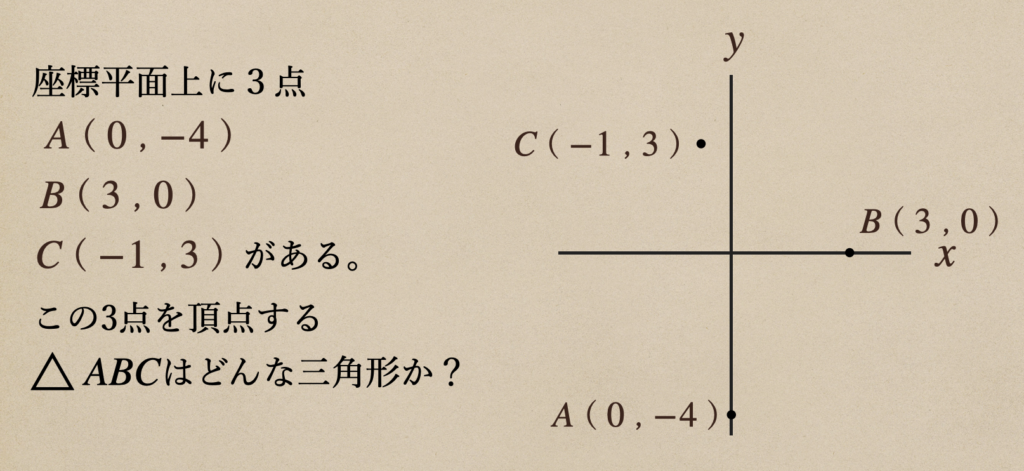
こんな風に、座標から三角形の形を考えていくってことだね。
ここでは、三平方の定理を題材としているので、定理が成り立つような
位置に点が置かれているんだけど、まず、確認することとしては
線分の\(AB\)、\(BC\)、\(CA\)の長さを求めて行ってみよう。
<\(AB\)の長さ>
\(AB^2=3^2+4^2\)
\(AB^2=9+16=25\)
\(AB=5\) \(AB>0\)
<\(BC\)の長さ>
\(BC^2=4^2+3^2\)
\(BC^2=16+9=25\)
\(BC=5\) \(BC>0\)
<\(CA\)の長さ>
\(CA^2=1^2+7^2\)
\(BC^2=1+49=50\)
\(BC=\sqrt{50}=5\sqrt{2}\) \(BC>0\)
\(AB:BC:CA=5:5:5\sqrt{2}=1:1:\sqrt{2}\)
よって、\(\triangle{ABC}\)は直角二等辺三角形である。
2点間の距離を求めのに、図形に線分を引いてみると、それぞれの線分っていうのが
直角三角形の斜辺になっているんだね。そして、斜辺以外の辺の長さは座標から
求めることができて、三平方の定理でそれぞれを求めていくことが
できるってことになるんだね。
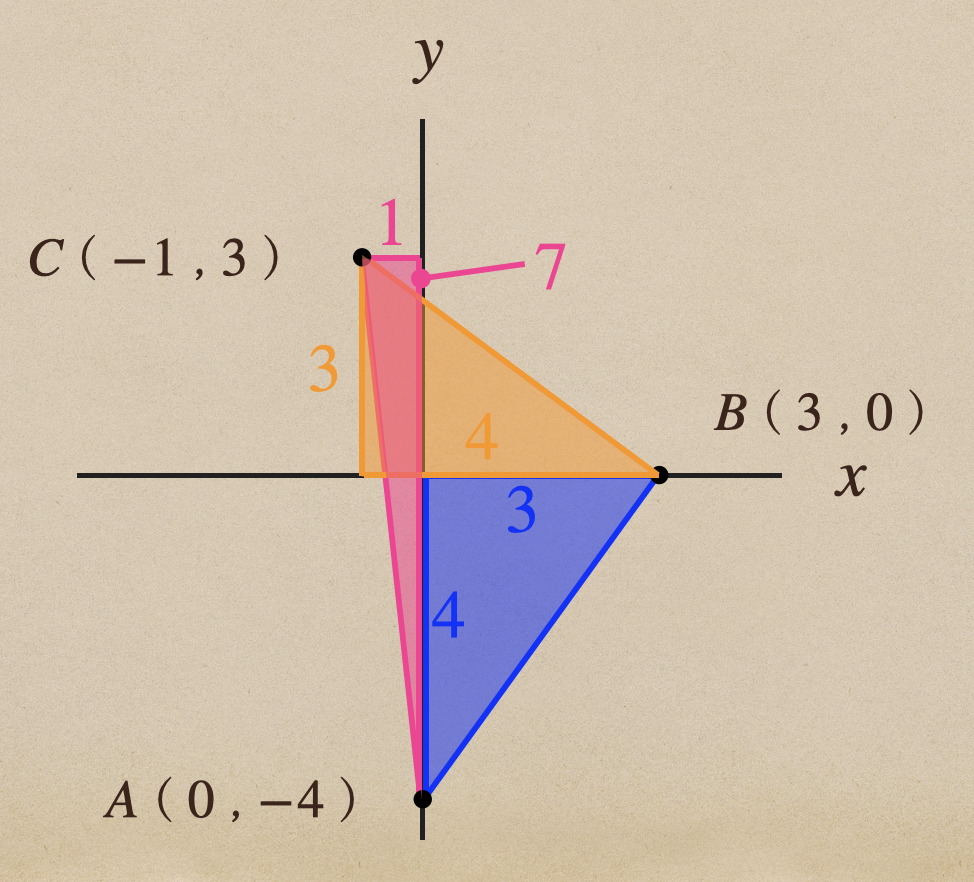
求められた各辺の長さから、前項の「2-1.平面図形の計量」で説明していた
特別な三角形の辺の比の関係にあったので、直角二等辺三角形ってことが
わかったってことになるね。
こういった、線分の長さから、どんな三角形かっていうのも知ることができるんだね。
3.空間図形の計量
この三平方の定理は平面図形だけでなく、空間図形でも使用することができて
立体のいろいろな部分の長さや、体積、表面積を求めていくことができるんだね。
・直方体の対角線を求める
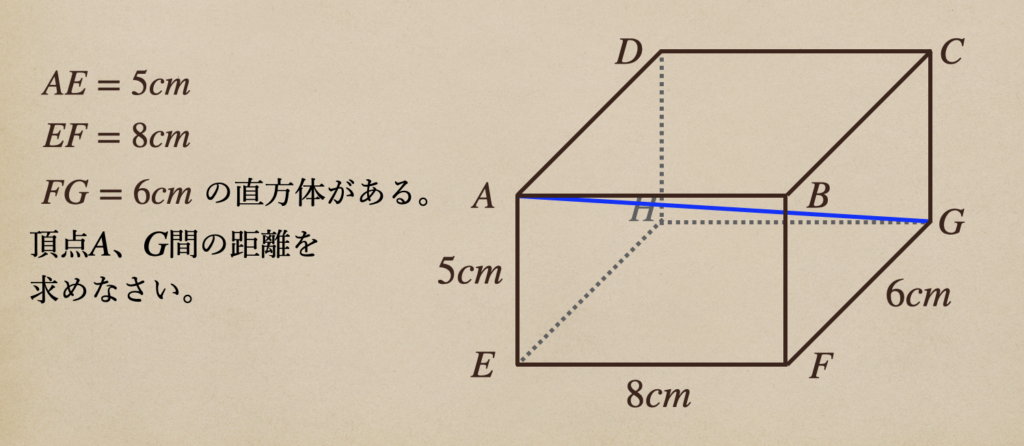
立体の対角線を求めようとするなら頂点の\(A\)、\(E\)、\(G\)を線で結んだ三角形を作って
あげて、その三角形っていうのが直角三角形になっているので\(AE\)の長さは\(5cm\)と
わかっていて、\(EG\)がわかっていないので、これを求めてあげる必要があるんだね。
そして、\(EG\)を求めてあげようと思うと、\(\triangle{EFG}\)から三平方の定理を
使って、求めていくことができるよね。
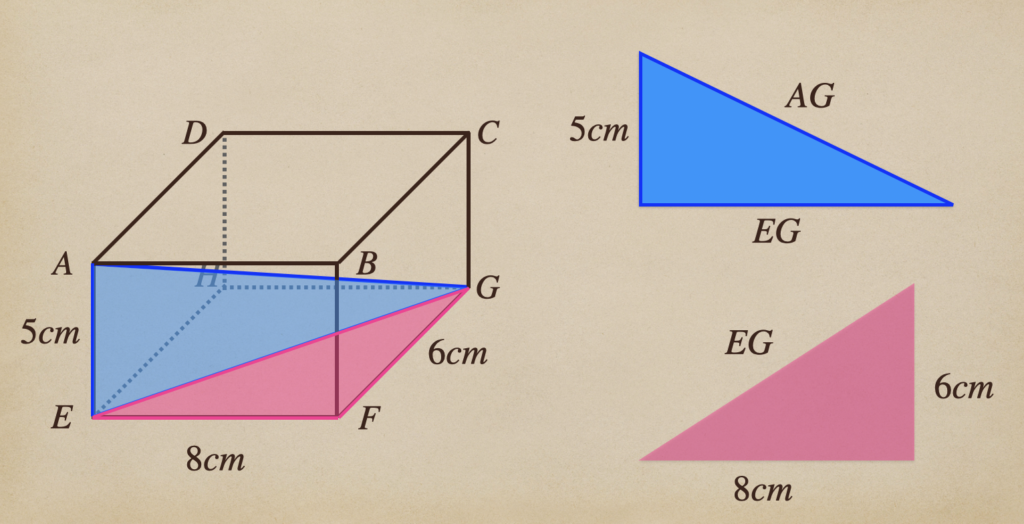
\(EG^2=8^2+6^2=64+36=100\)
\(EG=10\) \(EG>0\)
\(AG^2=5^2+10^2=25+100=125\)
\(AG=\sqrt{125}\) \(AG>0\)
\(AG=5\sqrt{5}\)//
立体でも、平面図形として1面ずつ見ていくことでそれぞれの長さを
求めていくことができて立体の対角線も求めることができるんだね。
・立体の体積と表面積
今度は、立体の体積や表面積について見ていきますね。
立体って言ってもいろいろあるんだけど、ここでは四角すいについて見ていきますね。
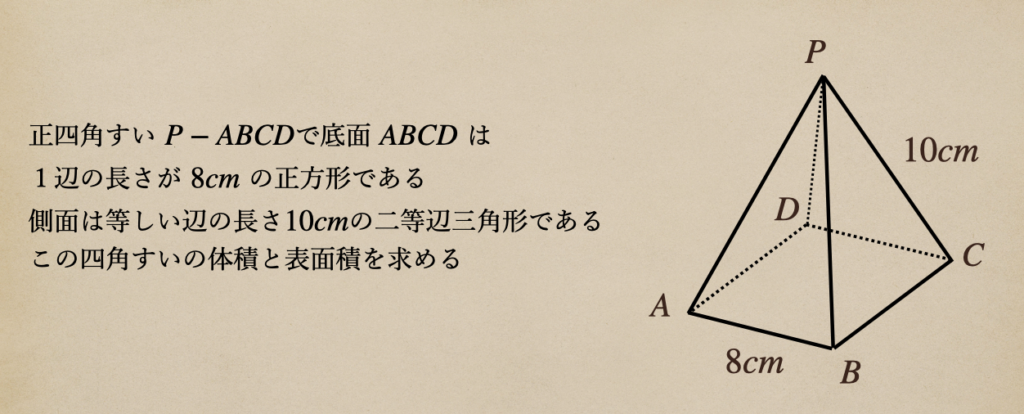
この図形の体積と表面積を求めるってことだね。
まずは表面積になるんだけど、これは側面の4つの三角形の面積と底面の面積の
合計が表面積になるってことだね。
側面の三角形の面積を求めようとすると、高さがわからないと求めることができないよね。
底辺は\(8cm\)ってことで高さが分かれば面積を求めることができるよね。
この三角形は斜辺が\(10cm\)の二等辺三角形ってことなので頂点\(P\)から底辺に
垂直に線を引いてあげた線分の長さが高さってことになるので、ここを三平方の定理で
求めてあげればいいね。
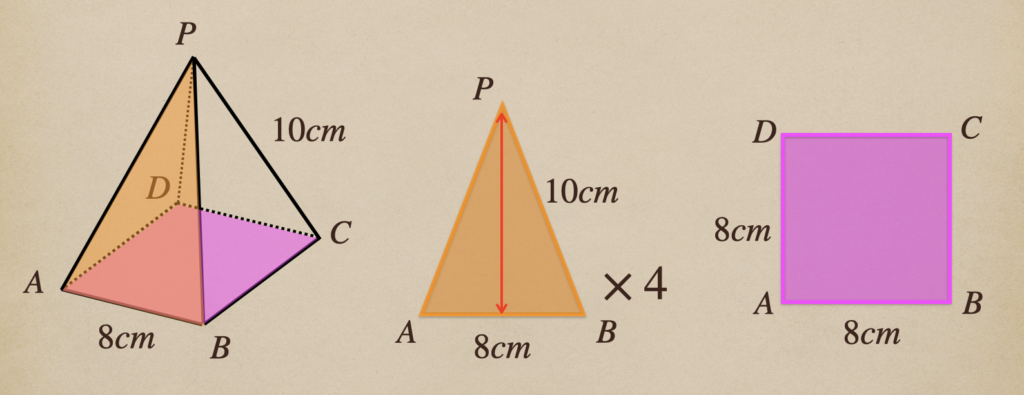
\(\triangle{PAB}\)の高さ\(h\)は斜辺\(10cm\)として、\(AB\)の半分\(4cm\)の
三角形から三平方の定理が使って
\(10^2=h^2+4^2\)
\(100=h^2+16\)
\(h^2=84\)
\(h=\sqrt{84}=2\sqrt{21}\) \(h>0\)
三角形の面積:\(8×2\sqrt{21}×\frac{1}{2}=8\sqrt{21}\)
四角形の面積:\(8×8=64\)
表面積:\(8\sqrt{21}×4+64=32\sqrt{21}+64\)//
これが表面積の求め方と解になるね。
次は体積を求めるんだけど、体積を求める公式は「低面積×高さ×\(\frac{1}{3}\)」で
求めることができるよね。ここでポイントはやっぱり「高さ」になるよね。
四角すいの高さは頂点\(P\)から底面\(ABCD\)に垂直に落とした線分が
高さってことなので、図にしてみると。。。
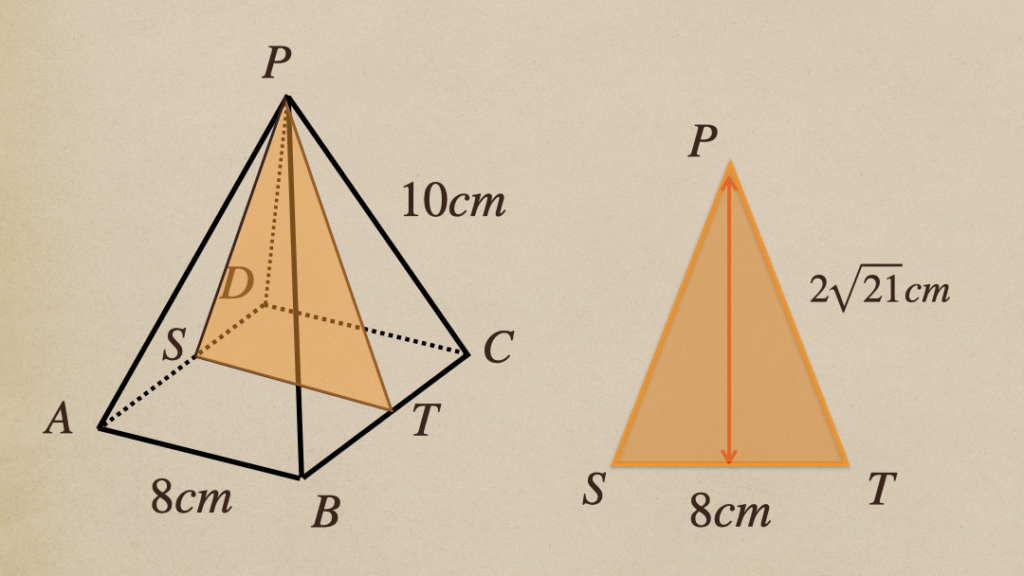
\(AB\)と\(BC\)の中点を\(S\)、\(T\)としたとき、\(\triangle{PST}\)として
見てあげて、この三角形の高さを求めてあげれば、四角すいの高さってことに
なるね。
\(\triangle{PST}\)の高さを\(h\)とする
三平方の定理から
\((2\sqrt{21})^2=h^2+4^2\)
\(84=h^2+16\)
\(h^2=68\)
\(h=\sqrt{68}=2\sqrt{17}\)
正四角すいの体積=低面積×高さ×\(\frac{1}{3}\)より
\(64×2\sqrt{17}×\(\frac{1}{3}=\frac{128}{3}\sqrt{17}\)//
こんな風に三平方の定理を使ってあげれば、立体の体積、表面積を求めていくことが
できるんだね。
今までに習った単元でも三平方の定理っていうのはいろいろと関わりがあるので
しっかり、理解して覚えておこう。
今回は、ここまでになります。
ここまでの記事が良かったと思ったらここをクリックしてね。
質問なんかがあった場合はコメントにお願いします。
では、また、さようなら。


コメント