どうも、こんにちはDKです。
今回は中学1年生の数学で習うデータの活用についてやっていきますね。
データっていうのは資料のことだね、資料の活用っていう言い方で習っている人も
いるかもだけど、内容は一緒になっているよ。
このデータの活用っていうの、中学ではサラッと習って終わっているかもしれないけど
このデータを見て、それを表やグラフにするって言うのは大人になってからの方が
使用する機会が増えるんだね。
何事もトライ&エラーで、繰り返し行なっていってベストなものを導き出すってことを
やっていくことがあるんだけど、ただ繰り返して行なっていくだけだと
エラー(失敗)を続けるだけになっちゃうよね?そんな時、エラーの情報をまとめ
それをもとに、何が悪かったのか、次はここを変えてトライするって言うのを
繰り返すことで、成功に近づいていくんだね。
ここで言うエラーの情報(データ)を元に分かりやすくした表やグラフっていうのを
活用することで、分析をしやすくなったりするんだね、こんな機会がこれからも
どんどん出てくるからここで習うデータの活用をしっかり学んでいってください。
それじゃあ、まずは度数分布についてやっていきますね。
度数分布
度数分布については動画でも公開しているよ。※音が出るから注意して
下の表は四つ葉のクローバーをある高さから落としてから地面に着くまでの
時間(滞空時間)をまとめたものになってるよ。
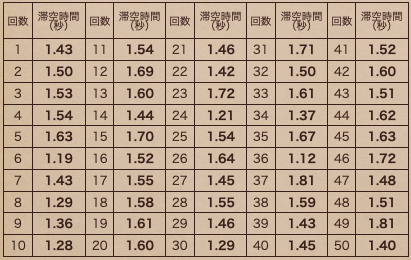
こんな風に行った作業に対して、結果を表にしているんだけど
このままだと、見にくいよね。そんな時に、整理してみるとどうなるかな?
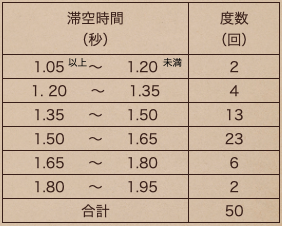
滞空時間を0.15秒ごとに区間を区切り、それぞれの区間にある回数をまとめた表になるんだ。
この1つ1つの区間を「階級」っていう言い方をするんだ
上の表の場合、階級の幅は0.15秒で階級の個数っていうのは6個ってことになるんだね。
そして、各階級に入るデータの個数を、この階級の「度数」って言うんだ。
度数っていうのは、階級の幅に含まれるデータの数を書く必要があって
この階級っていうのは 〜以上、〜未満となっていて
〜以上のところはその数字が含まれて、〜未満っていうところはその数字が含まれないので
度数を数えるときは、注意しよう。
そして、上の表のように階級に応じて、度数を整理した表っていうのを
「度数分布表」っていうんだね。
さらにこの「度数分布表」っていうのをグラフに表すことができるんだけど
横軸に滞空時間、縦軸を度数(回数)としてみてこんなグラフが書くことができるんだね。
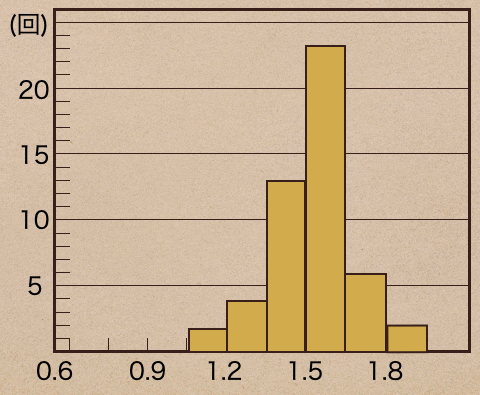
この階級の幅を横、度数を縦の軸にして長方形で表したグラフを「ヒストグラム」っていう
言い方をするんだね。
このヒストグラムにすることで、このデータも見やすくなったよね。
ただ、こんな時はどうなるかな?
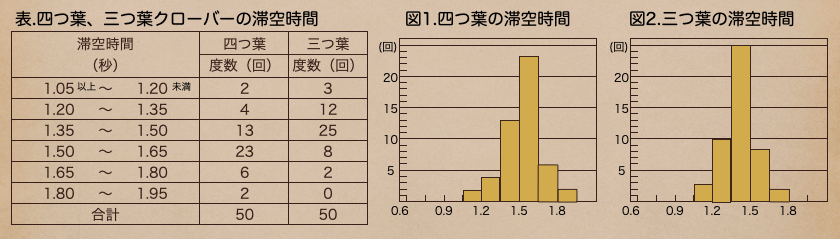
四つ葉のクローバーと三つ葉のクローバーのそれぞれの滞空時間の度数分布表から
ヒストグラムのグラフを表して書いたんだけど、ヒストグラムで表して
この2つのデータを見比べると、どういった違いがあるのかっていうのが
すぐには、分かりにくいよね。
この2つのヒストグラムを重ねて1つのグラフで見ようとしても、長方形が重なってしまって
余計に見にくくなっちゃうよね。
こんな時は、ヒストグラムのそれぞれの長方形の上の辺の中点を線で結んで表す方法が
あるんだ、そうすると…
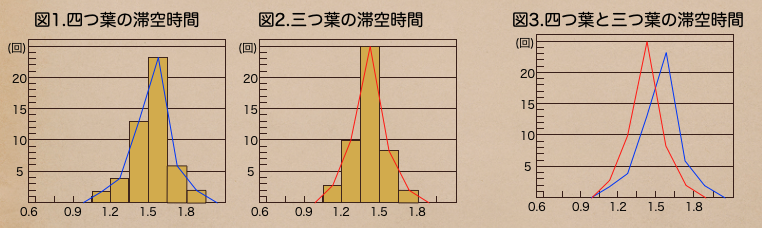
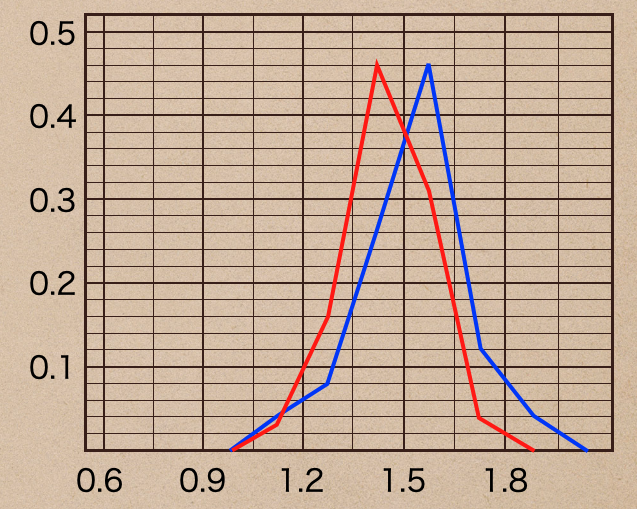
四つ葉のクローバーのヒストグラムを線で結んだ折れ線を青線で
三つ葉のクローバーのヒストグラムを線で結んだ折れ線を赤線で
書いたものを1つのグラフい合わせると2つのデータの比較が
しやすくなったよね。
このように折れ線グラフで書くのを「度数分布多角形」って言うんだ。
この度数分布多角形を書く時の注意は両はしのデータがないところは
度数「0」として、線分を伸ばして書く必要があるので、忘れずにしておこう。
こうすることで、2つのデータを見比べて三つ葉のクローバーの方が
滞空時間が短くなっていることがわかったりするってことなんだね。
今度は、こんな度数分布表があった場合どうなるかな?
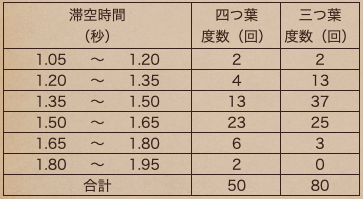
さっきと同じで四つ葉のクローバーと三つ葉のクローバーの度数分布表なんだけど
今回の表は三つ葉のクローバーの度数の合計っていうのが80回になっているよね?
四つ葉のクローバーは?っていうと、50回ってなっていて
それぞれの滞空時間を計測した回数っていうのが違っているよね。
この時、四つ葉と三つ葉で同じ階級の度数どうしをそのまま
比較してもいいのか?ってことだね。
答えはダメってことなんだね、計測した回数が違うとそれぞれの階級における
度数っていうのは比較できないってことなんだね、
今回みたいに50回、80回っていうと、そこまで差もないし
比較することができるかもしれないんだけ、この差がもっと大きな場合も
同じことが言えるかな?例え三つ葉のクローバーの計測を1000回やったとしたら
階級の度数が500回ってなってた場合、50回の計測を行ったものと
一緒に比較なんてできないよね。
じゃあ、こう言った場合はどうするのかっていうんだけど
この場合は、各階級の度数を全体の計測した回数で割ってあげることで
全体の度数の割合っていうのがわかるんだね。
この各階級の度数の全体に対する割合っていうのをその階級の
「相対度数」っていう言い方をするんだね。
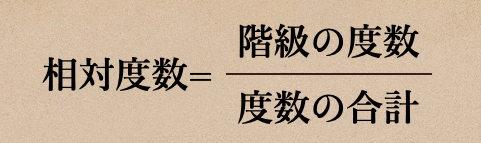
この割合っていうのは、ある階級における1回あたりの度数を
表しているってことになるんだね。
さっきの、度数分布表を相対度数で表して見てみよう。
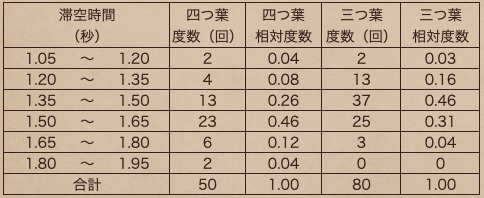
相対度数で表したことで、初めて、この四つ葉のクローバーと三つ葉のクローバーを
比較することができるんだね。
そして、この相対度数もグラフ(ヒストグラム、度数分布多角形)として
表すこともできるんだ。
度数分布表は階級は横っていうのはそのままなんだけど、
相対度数を縦で表して表にしているってことなんだね。
度数分布ってところでは、データから度数分布表やヒストグラム、度数分布多角形に
することで、データを分かりやすくなるようにしているんだね。
初めのうちは、表やグラフにすることはむずかしいかもしれないけど
色々なデータを表やグラフにしていくことで覚えていくことができるよ。
代表値と散らばり
ここからは、データにおける代表ちと散らばりについてやっていきますね。
動画でも、解説しているのでそちらも見てみてください。(注:音が出るよ)
下の表っていうのは、陸上選手2名が20回100mを走った時の記録を表にしているんだけど
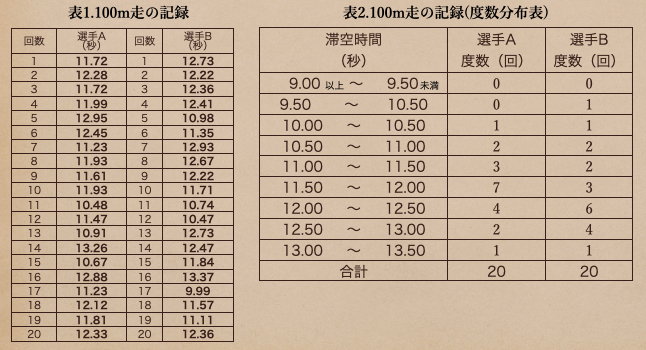
この2人の選手を見た時、どちらが早いのかっていうのが、この表からは判断がむずかしいよね。
このようなデータの特徴を表す数値として一般的なのが「平均値」になるんだね。
この平均値を求める式としては…

で、求めることができるんだね
上の表の平均値を求めるとなると
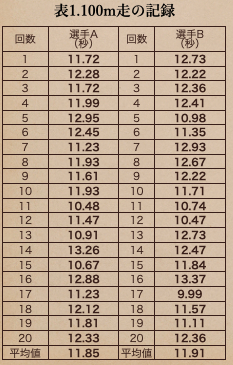
ここでは平均値なんかを求める時って言うのは、小数第2位までにして表しているんだね。
他にはデータの値全体を1つの代表を定めて、これを基準として
判断したりすることがあるんだね。これを「代表値」って言うんだね。
他にはデータを値の大きさの順番に並び替えて、その中央の値を
「中央値(メジアン)」って言うんだね。
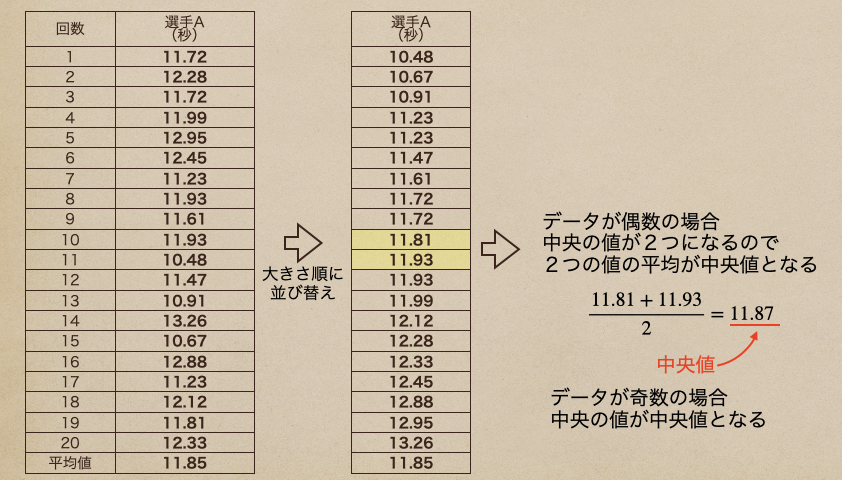
データの数によって、中央値の求め方って言うのは変わるので注意しておこう。
このデータの中央値をデータの代表の値にしようって決めたら
代表値は17.78になるってことだね。この代表値はデータの内容によって
決めることなので、必ずしも【代表値=中央値】とはならないってことも覚えておこう。
今度は、あるクラスの生徒の靴のサイズを調べたところ下の表の結果だったとき
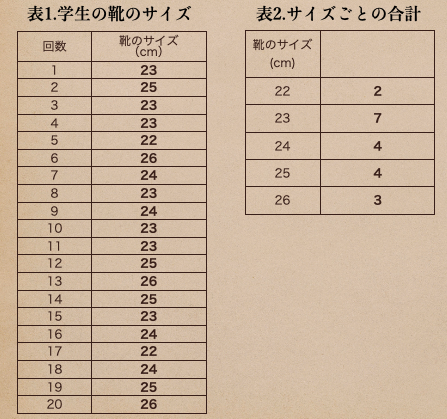
こんなデータにまとめられたとするね。
今回のように靴などの製造の場合っていうのは、できるだけ多くの数を
使用されているサイズを決めて、製造数の調節を行なったりするんだね。
このようにたくさんの人が使用しているサイズのことを「最頻値(モード)」って
いうんだね。上の表の最頻値は、23cmになるってことだね。
最頻値っていうのは階級で表している度数分布図でも決めることが
できるんだけど、その場合、階級の真ん中の値を「階級値」って言って
度数が多かった階級の階級値っていうのが最頻値になるってことだね。

上の図のように度数分布表で表したものから、平均値を求める必要が
あったとした場合。度数分布表っていうの階級別に度数で表されていて
それぞれのデータの値っていうのは、わからないよね。
度数分布表から平均を求めるってなった場合は、階級値っていうのが
その階級の値と見なして度数をかけてあげて、その階級の合計っていうのが
計算できるんだね。

それぞれの階級値に度数をかけてあげて、その合計から平均値を
計算してあげるってやり方だね。
データっていうのいろいろあるんだけど、AさんとBさんがそれぞれお団子を
10個ずつ作っていて、その重さを測ったところ次のような結果になったんだね。

Aさん、Bさんそれぞれの作ったお団子の重さの平均値と中央値を調べてみたら
上の通り、全く同じ値になったんだけど、このときAさんとBさんの作った
お団子はほぼ同じと言えるかな?
こういう時はデータの中の一番大きい値と一番小さい値の差を求めてみるんだ

この一番大きい値(最大値)と一番小さい値の(最小値)の差っていうのを
「範囲(レンジ)」って言うよ。
AさんとBさんのお団子の範囲はそれぞれ5.5gと13.9gと全然、違っているよね
こんな風に範囲が違う場合、度数分布やヒストグラムで書くとどうなるのか見てみよう。
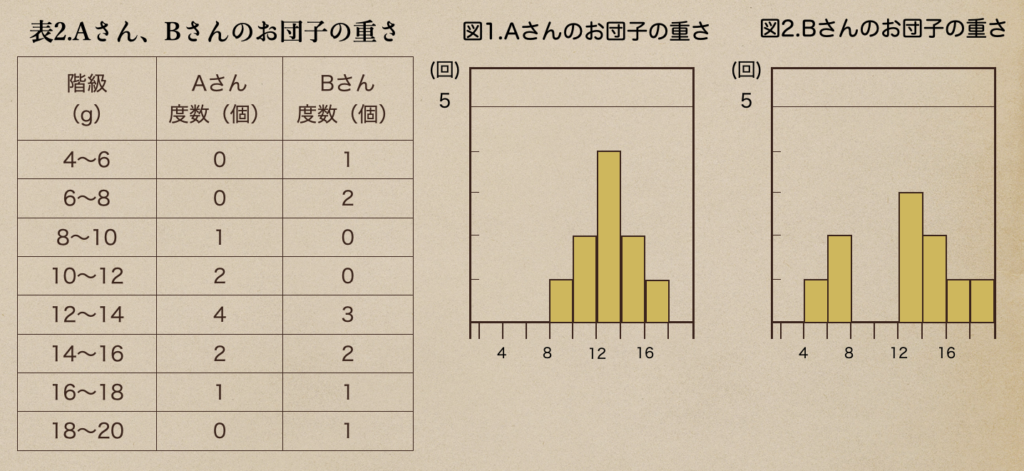
こうしてみると、Aさんの方は、きれいな山が1つできているのに対して
Bさんの方は、山が2つできていて、あまりきれいとは言えない形になっているよね。
このBさんのようなデータは「散らばっている」って言うんだね。
こんな風にデータだけ見ているだけだと、あまり気付けないことも
度数分布表やヒストグラムにすることで、どういった傾向のあるデータかってことが
わかったりするって言うことを覚えておこう。
近似値
次は近似値についてやっていきますね。
まずは、下の図の線分ABの長さって何mmになるかな?

40mm ? いや、39mmかな?もう少し細かく見てみよう。
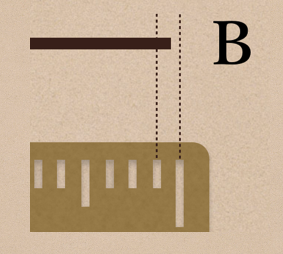
実際は39mm より長くて、40mm よりは短い長さってことだね
この線分ABを\frac{1}{10}まで読み取って 39.7mm って表すこともあるよね
ただ、測定っていうのはどんだけ精密に測ったとしても真の値と
等しくなっているのかっていうのはわからないんだね。
こんな風に測定した値みたいに真の値に近い値のことを「近似値」っていうんだね。
円周率の3.14って言うのも近似値になるよ。
そして、近似値から真の値を引いた差を誤差って言うんだね。
誤差 = 近似値 – 真の値
で計算することができるよ。
さっきの線分ABの長さの近似値40mmっていうのはcmで表すと
4cmってなるよね。これをmmの位までを意味のある数字するために
4.0cmと表すことがあるんだね。
近似値を表す数で、意味のある数字を「有効数字」って言って
その数字の個数を、有効数字の「けた数」って言うんだね。
はい、ではここまでがデータの活用についてでした。
ここまでの記事が良かったと思ったらここをクリックしてね。
質問なんかがあった場合はコメントにお願いします。
では、またさようなら。




コメント