どうも、こんにちはDKです。
ここからは中学2年生で習う数学について基礎となるところを解説しているよ。
2年生の数学はこの式の計算をしっかり、できるようにしていかないと
その後の、単元にはついていけなくなっちゃうので、しっかり基礎を身につけて
次に進んでいけるようにしていこう。
単項式と多項式
動画でも解説しているよ。(音が出るので注意して。)
ここでは、少し言葉を覚えていこう。
まずはおさらいになるんだけど、「項」って何かわかるかな?
「項」っていうのは…
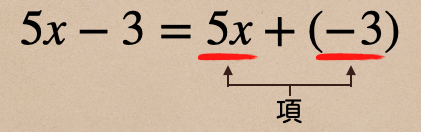
この式の場合だと、\(5xと-3\) っていうのが「項」になるんだね。
中学1年生では、\(5x\) を文字の項、\(3\) を数の項っていう言い方をしたりしていたよね。
それと、単項式、多項式っていうのがあって、それっていうのが…
単項式:項が1つだけのもの
多項式:項が2つ以上のもの
ってことで、どんな式が単項式、多項式かっていうと
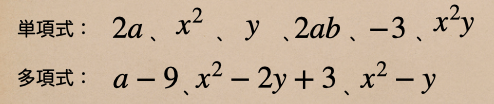
ようするに、項どうしを足したり、引いたりしていない式を単項式で
項どうしを足したり、引いたりしているものを多項式っていうんだね。
多項式の \(x^2-2y+3\) の中で文字を含んでいない \(3\) のことを定数項っていう
言い方するってことも覚えておこう。
定数項:多項式で文字を含んでいない項
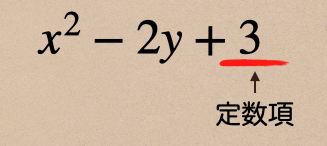
単項式で、かけあわされている文字の個数を単項式の次数っていうんだね。
多項式では、各項で次数が最も高い項の次数を多項式の次数っていうんだね。
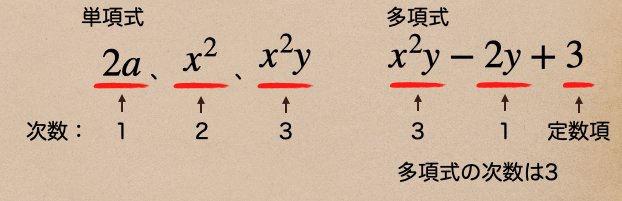
この次数っていうのが、1つの式を1次式、2つの式を2次式っていうんだね。
同類項
次は同類項についてやっていきますね。この同類項っていうのが
この単元「式と計算」のポイントになってくるところになるので
しっかり、どういったものなのかを理解していってくださいね。
同類項:多項式で同じ文字が同じ個数かけ合わされている項
ってことで、それっていうのが
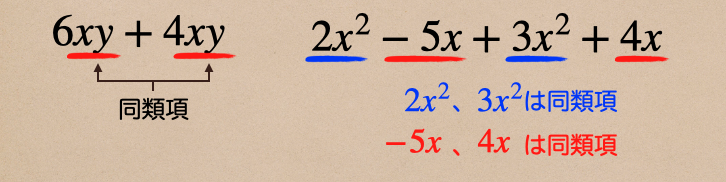
ってことなんだね。こんな風に多項式の中で、同類項っていうのがあって
この同類項どうしっていうのは、まとめて式を簡単にして行くことができるので
その計算の方法を見ていってみよう。
その計算方法っていうのが中学1年生で習った分配法則っていうのを使うんだね
分配法則っていうのは
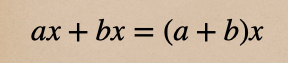
こんな式で \((a+b)\) を \(x\) でそれぞれにかけてあげればいいってやつだったよね。
これを今回は上の式のように、\(ax+bx\) の同類項である \(x\) を外に出して
\((a+b)x\)って式にしてあげるってことだね。
これを同類項を説明したときの式に当てはめてあげると…
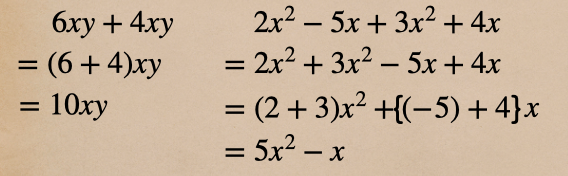
こんな風に同類項どうしを分配法則でまとめてあげて、カッコの中を計算して
簡単な式にしてあげることができるってことなんだね。
ちなみに、右の式の \(5x^2-x\) の \(x^2\) と \(x\) って言うのは同類項ではないので
間違えないようにしよう。
多項式の加法、減法
同類項どうしをまとめて簡単にするってことを理解してもらえたかと
思うので、今度は、多項式の加法、減法についてやっていくね。
加法っていうのは足す(+)ことで減法は引く(ー)ことだったよね。
加法:(1)\(6x+y+1\) に \(x-2y-3\) を加えた和
減法:(2)\(6x+y+1\) から \(x-2y-3\) を引いた差
この式をそれぞれ計算してみよう
まずは、(1)の加法を式にすると \((6x+y+1)+(x-2y-3)\) ってことだね。
これを計算すると
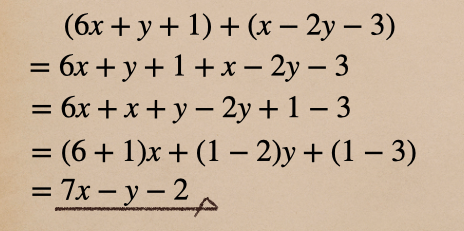
ここでは、計算をていねいにするために、わざわざ同類項をまとめたり
分配法則でカッコにしたりしているけど
2行目の \(6x+y+1+x-2y-3=7x-y-2)\) としてしまっても問題はないよ。
ただ、計算間違いはしないように確実に計算するようにしよう。
また、こういった式って言うのは、こんな解き方もあるんだ
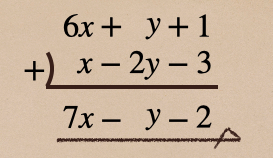
この方法は多項式を縦に並べて、それぞれ同類項を縦に計算をしてあげるっていう
方法になるんだね。
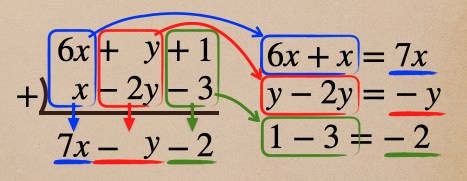
この縦書き計算っていうのは、次の連立方程式でも使う機会があるので、
やり方についてしっかり覚えておこう。
次は(2)の減法で、これを式にすると \((6x+y+1)-(x-2y-3)\) になるね
これを計算すると
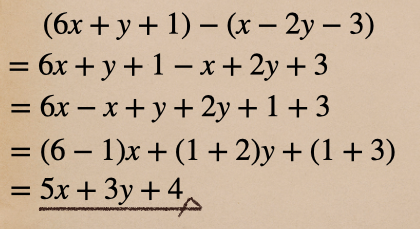
この計算で注意するところはカッコを外した時に \(x-2y-3\) の
それぞれに\(-1\) がかけられることになるので、符号が変わることに注意して計算しよう。
この式も、同じく、縦書きの計算ができて
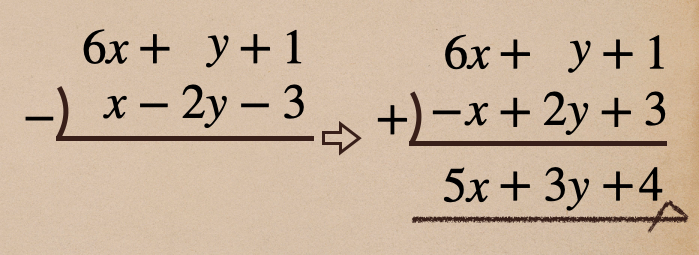
縦かきの計算で減法を行う場合は、一度、加法にするようにしよう
そのまま、減法から計算することは可能なんだけど、符号を入れ替えるのを
忘れてしまったりして計算ミスをしてしまうこともあるので、注意しておこう。
単項式と単項式の乗法
動画でも解説しているよ。(音が出るので注意して。)
この単項式と単項式の乗法を行うには係数の積と文字の積を求めてあげるんだね
ようするに
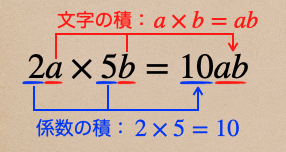
単項式っていうのは「係数×文字」になっているので、その積ってなると
「係数×係数×文字×文字」になって、それを計算してあげるってことだね。
この単項式どうしの乗法で注意が必要なのは累乗が含まれる計算をする場合だね。
累乗って言うのは指数で表されているもので、\(x^2\) や \(a^3\) のことだね。
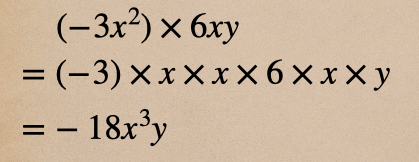
累乗が含まれていても、計算としては、係数の積、文字の積を行うことに
変わりはないので、落ち着いて、計算していこう。
累乗は同じ文字が指数の数だけかけられているってことなので
同じ文字の数を指数として表してあげればいいってことだね。
じゃあ、\(a^3×a^4\) の単項式どうしの乗法はどうやって計算しようか?

わざわざ、こんな計算していると、もっと指数の数が大きくなった時
計算が大変になっちゃうよね。
この累乗の乗法って言うのは単純に指数の数を足してあげることで
計算することができるんだね。
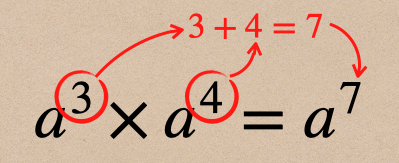
累乗っていうのは、指数の数だけ、文字がかけられているってことなので
その文字の数を表しているってことだよね。
なので、\(a^3\) は \(a\) が3個、\(a^4\) は \(a\) が4個あるってことなので
その乗法ってなると、 \(a\) が7個かけられているってことなるよね
なので、\(a^7\) になるってことだね。
これを、覚えておくと、累乗を含む単項式も計算がグッと楽になるから
ぜひ、覚えておこう。
単項式を単項式でわる除法
今度は、単項式どうしの除法ってことだね。
\(9ab÷3b\) を計算してみよう
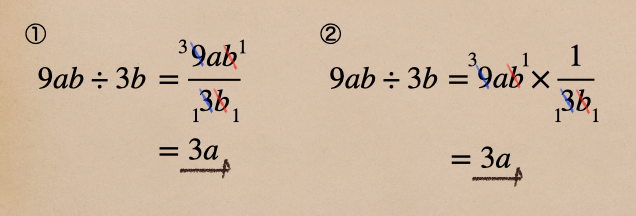
ここでは、2パターンの計算の仕方を紹介しているんだけど、
①の計算は分数の形にして計算していて
②の計算は除法(÷)を乗法(×)に変更してから計算しているってことなんだけど
①の計算も、②の計算もどっちの方法で計算してあげてもいいので
計算し易い方を選んで、計算して行くようにしよう。
ただ、この後に解説する分数を使った、除法なんでは①のように分数の形にするっていうのが
むずかしことになるので、計算に慣れていくっていうのであれば②の計算方法がいいね。
あと、累乗の除法っていうのは、累乗の乗法と同じ考え方で、除法の場合が
指数どうしを引いてあげればいいってことなるので、ここも覚えておこう。
次は、除法と乗法が混ざった計算について説明しておきますね。

乗法と除法が混ざった式の場合は、まずは除法を乗法にしよう。
ここで、注意が必要なのは\(-\frac{2}{3}a\)をどうやって逆数にするかってことなんだけど
係数が \(-\frac{2}{3}\) となっているよね、それに \(a\) がかけられているってことなので
これっていうのは \(-\frac{2a}{3}\) になっているってことなんだね
なので、これを逆数にすると、\(-frac{3}{2a}\) になるってことだね。
ここがしっかりと理解できていれば、あとは落ち着いて計算すれば、ミスなく
問題を解くことができるよ。
多項式と数の計算
多項式と数の計算っていうのは主に、乗法と除法になるんだけど
これっていうのは、中学1年生の文字式で習った内容になっているんだね。
ただ、中学2年生からはもう少し、計算がむずかしくなっているんだね。
ここでの基本となるのは
多項式と数の情報では、分配法則を使う
\(a(b+c)=ab+ac\) / \((a+b)c=ac+bc\)
ってことだね。これをふまえて計算してみよう
□多項式と数の乗法・・・ \(-3(4x-5y)\) を計算する
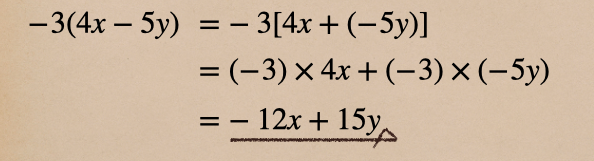
この計算での注意は、\(-3\) をそれぞれにかけるってことと
\(-5y\) を “\(+(-5y)\)” として考えるってことだね。
そして、\((-3)×(-5y)\) にしてあげるってことだね。\((-3)×5y\) としてはダメってことだよ。
□多項式を数でわる除法・・・ \((9x-12y)÷3\) を計算する
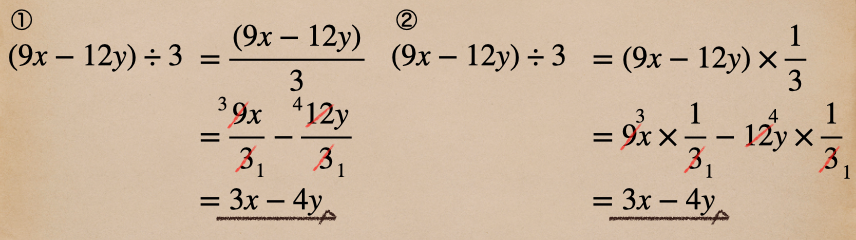
この除法でも、計算方法は2パターンあって
①式を分数の形にする
②逆数にして乗法(×)にする
だね、どちらの方法で計算してもオッケーってことだね
ただ、負の符号をかける時は注意が必要だね。
□カッコとふくむ式の計算・・・\(3(2x-6y)-5(x-3y)\) を計算する
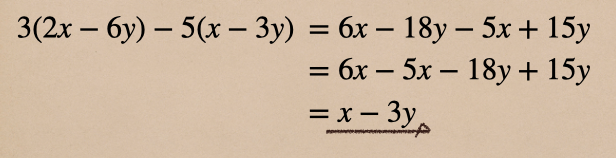
この計算はそれぞれを分配法則を使って計算して
あとは、同類項どうしを計算してあげるってことだね
ここでも、注意は負の符号がふくまれる項どうしをかける時だね。
□分数をふくむ計算・・・\(\frac{2x-y}{3}-\frac{x-3y}{2}\) を計算する
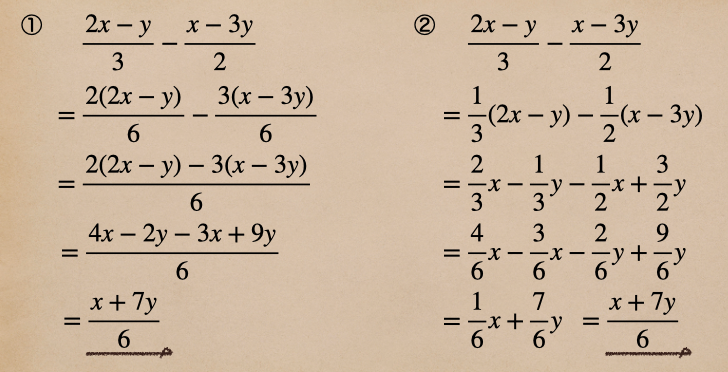
ここでも2パターンの計算方法があって
①通分して計算する
②分配法則を使用して計算する
どちらの方法で計算しても問題はないよ、両方のパターンでの計算の仕方をっていうのを
しっかり理解して、計算できるようにしていこう。
式の値
動画でも解説しているよ。(音が出るので注意して。)
ここも、中学1年生でならってきた代入を行なって式の値を求めるってことになるね。
1年生の時より式もむずかしくはなっているけど、考え方は同じだよ。
まずは、文字の値を代入して式の値を求めてみよう。

それぞれの文字に値を代入して、計算をしてあげれば式の値が求められるって
ことだったよね。
じゃあ、次は累乗をふくむ式の値についてやってみるよ。

累乗の場合は、どこに指数がかかっているかって言うのが大事で
今回の場合は \((-2)^2\) ってことだったので、\((-2)×(-2)=4\) と
正の数になるってことだね。あとは、計算間違いのないように
確実に計算をするだけだね。
今度は、多項式の加法、減法と乗法が混ざった式の場合になるよ。
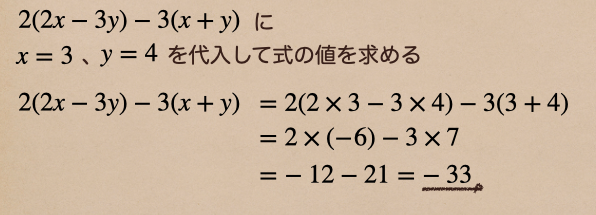
上の式ではそのまま、文字の値を代入して、数の項にしてから
計算をしていったんだけど、この式の場合だと式を簡単にすることができるよね。
式を簡単にしてから、文字の値を代入して式の値を求めた場合も見てみよう。
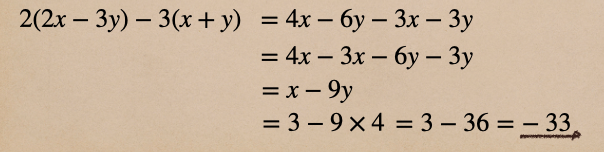
式を簡単にした方が、文字の値を代入する方が数の項の計算が簡単になったよね。
この式の場合、どっちの求め方でも問題はないので自分の得意な方でとければいいよ。
ここまでが、式と計算になるよ。いろいろな式の計算を解説したけど、
問題では、ここで解説した式の計算をまぜこんだ式を計算するようなものが出題されるから
1つ1つを確実に計算できるようになるまで、繰り返し問題を解いていってくださいね。
式の利用[数の性質]
今度は、式の利用[数の性質]ってところをやっていくね。
ここでは、文字を使って、「こうだから、こうなる」って言う説明をすることになるので
今までの計算を行うだけではないので、この『説明する』ってどう言うことなのかを
しっかり理解していってください。
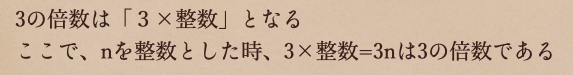
文字で式を表してみると、3nってなって、3×nになっているってことだよね。
だから、nの値がどんな数であろうと、最後には3をかけることになるので
結果、3の倍数ですよってことが言えるってことだね。
他にも、こんなことも言えるよ。
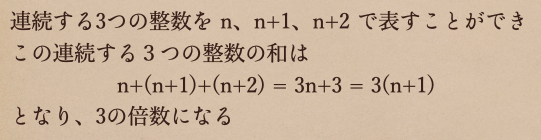
実際に、連続する整数 [3,4,5]や[13,14,15]の和っていうのは
5+6+7=18
13+14+15=42
と、どちらも3の倍数になっていることがわかるよね。
数字の計算だけだと、何パターンかの連続する3つの整数の和を計算して
どれも、3の倍数にあることを確認することができると思うんだけど
文字を使って考えてあげることで3の倍数であるってことがすぐにわかったよね。
こんな風に
文字を整数としてみたとき、整数についての
性質がすべての場合に成り立っていることを
文字式を使って説明することができる
ってことなんだね。
ここで、文字式を使って色々な数の表し方っていうのを紹介しておくね。
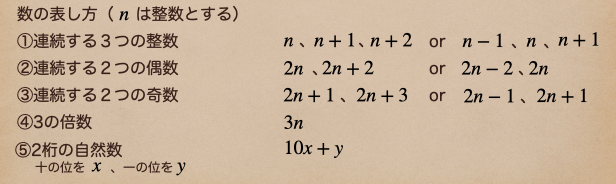
こんな風にして、文字式を使って数を表したりできるってことなんだね。
関係を表す式
□式による説明
文字式っていうのは、その文字式を書くだけでそれが何を言っているのかが
わかるものがあるんだけど、何かわかるかな?
それは、公式になるんだね。
公式ってその文字式で面積なんかを説明していることになるんだね。

円の面積は?っていうと半径×半径×円周率だよねこれを文字式で書くと
\(S=\pi r^2\) ってなるよね、これは円の面積の公式として表されていて、
一般的に面積は S 、半径は r 、円周率は π として表されているよね。
逆にいうと、\(S=\pi r^2\) は何を表している?って聞かれた時に
円の面積って答えることができるんだね、こんな風に文字式を見て
その式を説明することができるってことなんだね。
□等式の変形
ここに 等式:\(y=2x-21\) があって、これを\(x=O\) の形にしようとすると…

移行を使って、式を \(x=O\) の形にすることができたよね。こんな風に
初めの式を変形して \(x\) の値を求める式にすることを
「\(x\) について解く」と言う
こうすることで、\(y\) の値を代入してあげれば、\(x\) を求めることができるってことだね。
今回は、\(x\) について解いたんだけど、「OOについて解く」ってなると
「OO = 〜」となるように式をいこうしてあげる必要があるってことだね。
例えば、円錐の面積 \(V=\frac{1}{3}\pi r^2h\) をhについて解くってなると
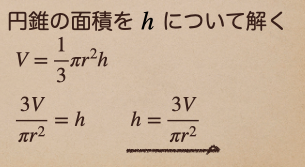
このように h=〜 の形にしてあげるってことですね。
〜=h って式でも同じことで、間違いではないんだけど数学の書き方の基本として
求める文字(ここで言うと h )は左辺に書いて「h=〜」ってして
書くようにしよう。
ここまでが式と計算についての解説となります。
ここまでの記事が良かったと思ったらここをクリックしてね。
質問なんかがあった場合はコメントにお願いします。
では、またさようなら。



コメント