どうも、こんにちはDKです。
今回は、中学2年生で習う、連立方程式についてやっていきますね。
この連立方程式からようやく、ザ・数学って感じになってくるので
しっかり、どう言ったものかを理解して自分のものにしていってくださいね。
連立方程式
まずは、連立方程式って何?っていうところからやっていきましょう。
動画でも、解説やっているよ。
まずは、こんな場合…
1袋2個入りのリンゴと1袋3個入りのオレンジを合計30個となる
式にして書くとすると

って書くことができる。
これは、\(2x\)がリンゴ\(x\)袋の時のリンゴの個数で、
\(3y\)がリンゴ\(y\)袋の時のオレンジの個数となって、その合計が30個になるよって
式になっているんですね。
こんな風に、\(2x+3y=30\)のような式を2元1次方程式って言うんですね。
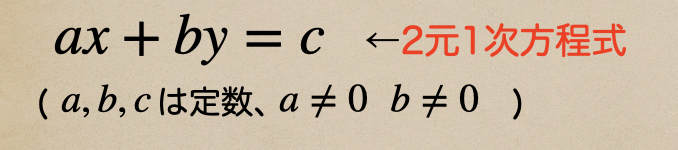
そして、2元1次方程式を成り立たせる、\(x\)と\(y\)の値の組みを解って言うんだね。
さっきのリンゴとオレンジの2元1次方程式の解を見てみよう。
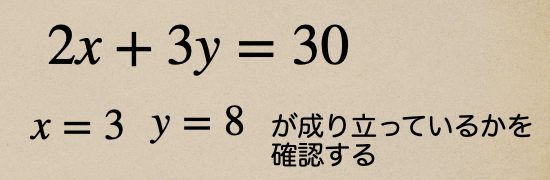
\(x=3\)と\(y=8\)が成り立つかを確認する場合は、\(2x+3y=30\)に
それぞれ、代入してみるんだね。そうすると…
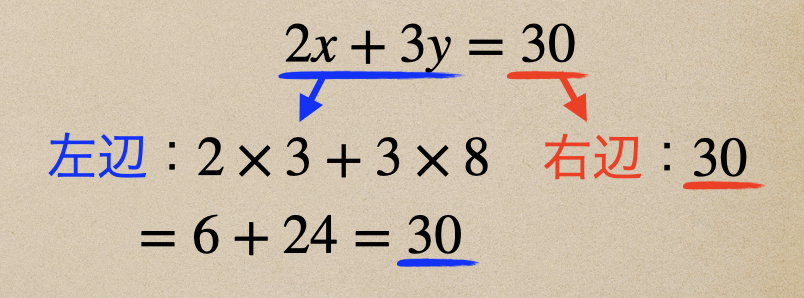
左辺の式に\(x\)と\(y\)を代入して値が30となって、右辺の値と同じになったよね。
左辺=右辺となっているので、\(x=3\)と\(y=8\)は2元1次方程式の解になるってことだね。
ちなみに、2元1次方程式\(2x+3y=30\)の解は他にもあるので
どんな解があるかを確認してみてください。
さっきのリンゴとオレンジの2元1次方程式っていうのは
1袋2個入りのリンゴと1袋3個入りのオレンジを合計30個となる
ってことだったよね。これにさらに
リンゴの袋とオレンジの袋の合計が13袋となる
っていうのを追加した場合、2元1次方程式で書くと

と表すことができるんだね。
この\(x+y=13\)の解は?っていうと、
\(x=1\)、\(y=12\)や\(x=6\)、\(y=7\)になるんだね。
じゃあ、この2つの方程式の両方を成り立たせる\(x\)と\(y\)の値の組みを求める時っていうのは
①1袋2個入りのリンゴと1袋3個入りのオレンジを合計30個となる
②リンゴの袋とオレンジの袋の合計が13袋となる
方程式で書く場合は
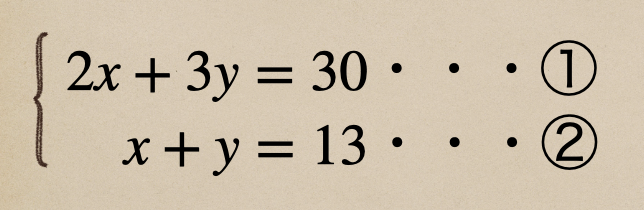
となって、これを連立方程式っていうんですね。
そして、この連立方程式っていうのは、それぞれの解から、2つの方程式が
成り立つものっていうのは、1種類しかないってことなんですね。
方程式①、②の解を書き出して、確認してみましょう。

これが、それぞれの2元1次方程式の解となっているんですね。この中で
同じ、解になっているのが1つありますよね。\((x,y)=(9,4)\)がそうですね。
なので、この連立方程式の解は\((x,y)=(9,4)\)ですよってことになるんですね。

解の書き方はいろいろあるんだけど、どの書き方でも正しいので、自分の書きやすい書き方で
解を表していこう。
今回は、それぞれの2元1次方程式の解を書き出して、共通する値が解ですって
求めてみたんだけど、ここで解として表したのは正の整数だけになっているんだね。
他にも、負の整数や、分数、少数でも書き出していくことはできるので
2元1次方程式の解っていうのは、いくらでもあることになるんだね。
それをわざわざ、書き出して共通の値を探し出すことなんて無理だよね。
なので、今度は連立方程式の解き方っていうのを解説していきますね。
連立方程式の解き方(加減法)
連立方程式っていうのは、解き方が2パターンあって、1つずつ解説していきますね。
まずは、連立方程式
\(4x+y=12\) ・・・①
\(x+y=6\) ・・・②
この連立方程式を見てみると、\(y\)の係数が等しいよね。
こんな時は①の各辺から②の各辺をひくことができるよね。
これを、ひとつ前の解説の式と計算でもやっていた、縦に計算する方法で
各辺を計算してあげるんですね。
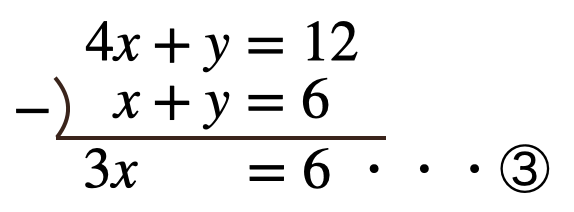
各辺でひいたことによって、③のように文字を1つだけ含む方程式にすることができたよね。
③から\(x\)の値を求めると。。
\(3x=6\)
\(x=2\) ・・この\(x\)の値が連立方程式の\(x\) の解となる
ここで、\(x\)の値を②の式に代入すると
\(x+y=6\)
\(2+y=6\)
\(y=6-2=4\)
となって、この連立方程式の解は\(x=2\)、\(y=4\)となるんですね。
こんな風に、\(x\)と\(y\)の連立方程式から\(y\)をふくまない方程式を導き出すことを
連立方程式から\(y\)を消去するっていうんだね。
そして、
2つの式の左辺と左辺、右辺と右辺を加法、減法して
1つの文字を消去する、この解き方を加減法という
この加減法は、連立方程式の片側の係数が同じであったりして加法、減法を
行うことで、片方の文字を消去できるときによく使われるんだね。
じゃあ、もう一つ連立方程式の解を加減法を用いて解いてみるね。
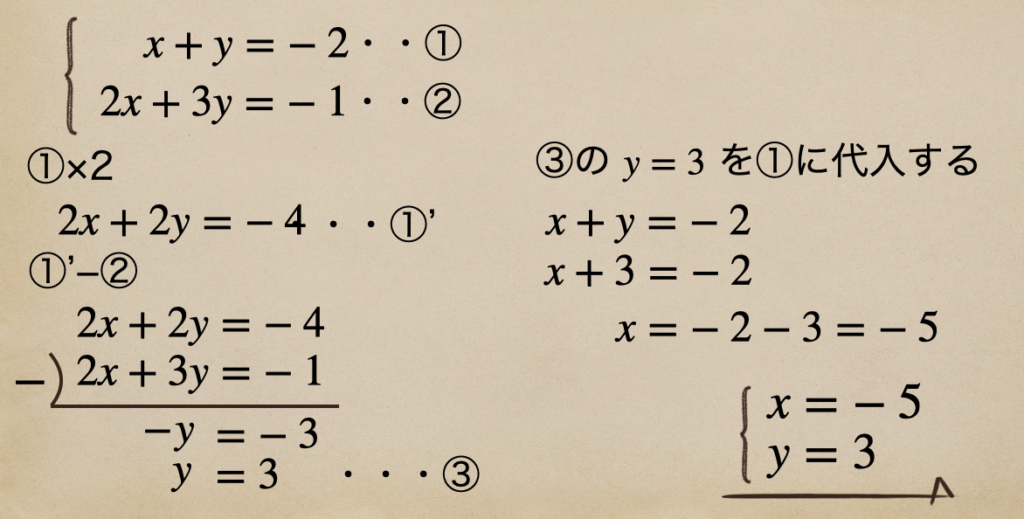
この連立方程式では\(x\)も\(y\)も係数が等しくないですよね、なので
この場合はまず、どちらかの係数を合わせてあげる必要があるんだね。
なので、①の方程式に2をかけてあげることで、\(x\)の係数を合わせてあげて
①’の方程式にしてるんですね。これで、\(x\)の係数が等しくなったので
①’−②をしてあげて、\(x\)を消去してあげて、残った\(y\)の値(③)が求められたよね。
そして、③の\(y=3\)を①の方程式に代入してあげて\(x\)の値を求めて
解は\(x=-5\)、\(y=3\)になったってことですね。
この連立方程式を解く場合っていうのは、上で紹介しているように
方程式に番号を振ってあげて、その番号をどうするっていうのを書きながら
計算をしていくようにしよう。こうすることで、自分が何をしたいのかっていうのを
整理することができるし、読み手(先生)なんかも、理解がしやすくなって
正しく採点してもらえるよ。わざわざ、言葉で細かく説明してもいいんだけど
そうするとテストとかでは、説明文を書くだけで時間を使ってしまって
時間がなくなって、最後まで問題が解けなくなるってことにもなっちゃうので
短く、的確にやっていることを説明しつつ、問題を解くようにしていくことを
意識していきましょう。
次はもう一つの方程式の解き方について解説していきますね。
連立方程式の解き方(代入法)
今度は、連立方程式の解き方のもう一つの方を解説していきますね。
こっちでは、この連立方程式
\(y=2x\) ・・・①
\(3x-y=6\)・・・②
で解き方の解説を行っていくよ。
この連立方程式のような場合、①の方程式に注目すると
\(y=2x\)ってなっているよね。これって、\(y\)は\(2x\)ですよって言ってるんだね。
ということは、②の方程式の\(y\)も\(2x\)に置き換えることができるよね。
ようするに
\(3x-y=6\)
\(3x-2x=6\)
\(x=6\)
こんな風に、文字を一つにすることができたよね。これっていうのが
\(y=2x\)を②の方程式に代入したことで、②の式から\(y\)を消去した
ってことなんだね。
代入して一方の文字を消去して解を導く解き方を 代入法 という
代入法は\(y=ax\)や\(x=by\)ってなっている時には使われやすいんだね。
もちろん、\(y=ax\)や\(x=by\)って式でなくても代入法は使うことはできるので
さっき、加減法で解き方を解説していた連立方程式を
代入法で解いたらどうなるか見てみよう。

方程式①と②のどちらで式から、\(y=OO\) 、 \(x=OO\)を解いても
問題ないんだけど、代入する式はあまり複雑にならないようにしておこう。
複雑な代入を行っていかないといけないってことになるので、
少しでも簡単に計算できるようにするようにしておこう。
いろいろな連立方程式の解き方
動画でも解説しているので、確認してみよう。(音が出るので注意してね)
いろいろな連立方程式っていうのは
□カッコがふくまれた連立方程式
□小数がふくまれた連立方程式
□分数がふくまれた連立方程式
□\(A=B=C\)となっている連立方程式
この4つになるんだ。それぞれ、解き方を見ていこう。
□カッコがふくまれた連立方程式
\(3x-5y=3\)・・・①
\(x-4(x-y)=-6\)・・・②
こんな風に、連立方程式の中にカッコが含まれている場合になるんだ。
こんな時は、カッコを外して式を簡単にするんだね
なので、②の式を分配法則を使って計算するんだね。
\(x-4(x-y)=-6\)
\(x-4x+4y=-6\)
\(-3x+4y=-6\)・・・③
②の式を③の式にまで、簡単にできたよね。
あとは、①と③の連立方程式を解いてあげればいいってことになるよね。
ちなみに、①と②の連立方程式の場合は、加減法、代入法の
どちらでやる方がいいかわかるかな?
それは、加減法ってなるんだ。式を並べてみてみると
\(2x-5y=-11\)・・・①
\(-3x+4y=-6\)・・・③
\(x\)の係数が①:\(3x\)、③:\(-3x\)になっているよね
①+③をすれば、\(x\)を消去することができるよね。
なので、この場合は加減法で解くほうがいいってことなんだね
もちろん、代入法で解くこともできるんだけど、複雑な計算をしないといけなくなってしまうので
あまり、おすすめはできないかな。
□小数がふくまれた手連立方程式
次は、小数をふくむ連立方程式だね。
\(0.3x-0.5y=-0.2\)・・・①
\(-5x+7y=2\)・・・②
①の式が小数になっているよね、このまま解いていくことはできるんだけど
もっと簡単に解く方法があるんだね、それは
①の式の両辺に \(×10\)をしてあげるってことですね。
方程式っていうは、左辺と右辺が等しい関係にある等式ってことですよね。
等式の場合は、両辺に同じ数をかけても等式は成り立つってことだったよね。
なので、①の式の両辺に \(×10\)ても、等式は成り立つってことなんだね。
\((0.3x-0.5y)×10=-0.2×10\)
\(0.3×10-0.5y×10=-0.2×10\)
\(3x-5y=-2\)・・・③
こんな風に\(×10\)してあげることで、小数の係数だったものが
整数がとして表されているよね。
あとは①と③の連立方程式を解けばいいってことになるね。
□分数がふくまれた連立方程式
今度は、分数をふくんだ連立方程式について見てみるよ。
\(\frac{1}{3}x-\frac{1}{4}y=2\)・・・①
\(2x+y=2\)・・・②
分数の場合は小数と同じように、まずは分数を整数にしてあげるんだね。
①の式の両辺に\(3\)と\(4\)の最小公倍数である\(12\)をかけてあげると
分数である\(\frac{1}{3}x\)と\(\frac{1}{4}y\)の分母をはらうことができるんだね。
実際に、計算式を見てみよう
\(\frac{1}{3}x-\frac{1}{4}y=2\)
\((\frac{1}{3}x-\frac{1}{4}y)×12=2×12\)
\(\frac{1}{3}x×12-\frac{1}{4}y×12=2×12\)
\(4x-3y=24\)・・・③
これで、式が簡単になったので①、③の連立方程式を解いていけばいいってことだね。
□\(A=B=C\)となっている連立方程式
次は、こんな方程式の場合はどうなるか、考えてみよう。
\(8x+3y=3x-2y=5\)
この方程式っていうのは、\(8x+3y\)と\(3x-2y\)と\(5\)っていうのが
お互いが等しいことを表しているんだね、なので、こんな連立方程式がつくれるんだね。
\(8x+3y=5\)・・・①
\(3x-2y=5\)・・・②
3つがそれぞれで等しいってことなので、こんな連立方程式をつくることもできるんだね。
\(8x+3y=3x-2y\)・・・③
\(3x-2y=5\)・・・④
\(A=B=C\)の形の方程式は
3通りの連立方程式をつくることができて
どの連立方程式の解は同じになる
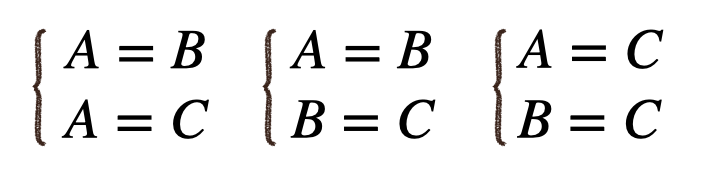
なので、\(A=B=C\)のような式は3通りのうち、どの連立方程式をつくって
解いてもいいってことになるんだね。
連立方程式の利用
動画でも解説しているのでそっちもみてみて下さい。(音が出るので注意してね。)
連立方程式では、計算問題も解き方を自分なりに考えて出来るだけ
簡単に、早く解けるようにしていくことが大事になってくるんだけど
他にも大事になってくるのが、ここで解説する連立方程式の利用になるんだ。
それっていうのが、文章から連立方程式をつくるってことなんだね。
ここでは、その文章問題の代表となる
□代金に関する問題
□割合の問題
□速さの問題
について解説をしておくね。例題をもとにどのように連立方程式をつくるのかっていうのも
説明しているよ。
まずは、文章問題をやっていく上で、押さえておくポイントを言っておくよ。
・何を\(x\)と\(y\)にするか考える
・等しい関係を見つけて、連立方程式をつくる
・つくった連立方程式の解が正しいか確認する
ってことなんだね。この3点をふまえて次に進もう。
□代金に関する問題
代金に関するっていうのは、OO円のリンゴを△△個買ったってのが
よくあって、このOOか、△△ってところのどちらが、わかっていないので
そこに、\(x\)や\(y\)を当てはめて式を作るってことなんだね。
それと、個数と金額っていうのをかければ代金になるってこともしっかり
理解しておこう [個数]×[金額]=[代金]ってことだね。
例題を解いてみよう。

この問題を考えてみよう。まずは、どこを\(x\)、\(y\)にするかで
この問題で聞かれているのは「りんごとぶどうの値段は?」と聞かれているので
りんごとぶどうの値段がわかっていないことなので
ここを\(x\)、\(y\)にしてあげればいいですね。
りんごの値段 :\(x\)、ぶどうの値段:\(y\)としていきましょう。
問題の中で「りんご5個と、ぶどう3個買った時は1050円」ってことなので
これを方程式で書くと、\(5x+3y=1050\)ってなるんですけど
これっていうのが

それぞれを細かく書くと、青字は個数、オレンジは値段(単価)、赤字は代金となっていて
この方程式っていうのは[代金+代金=代金]の等式になっているってことがわかるよね。
こんな風に、方程式をつくる場合は、左辺と右辺が同じものになっていないといけないってこと
なんですね。これが[個数+個数=代金]とかにならないように注意しよう。
もう一つの「りんご3個と、ぶどう6個買った時は1260円」っていうのは
\(3x+6y=1260\)となるんですね。
これも、同じく[代金+代金=代金]になっているってことですね。
これで、二つの方程式ができたので
\(5x+3y=1050\)・・・①
\(3x+6y=1260\)・・・②
の連立方程式ができたってことですね。これを解いていくと…

計算問題の連立方程式を解く場合は、解は\(x=OO\)、\(y=OO\)と書いていたんだけど
文章問題の答えっていうのは、りんごとぶどうの値段を書かないと
正解とはならないので注意しておこう。また、その際の単位を合わせることも
重要になってくるので、注意しておこう。
□割合の問題
割合に関する問題は、苦手って人も多いと思うんだけど
それっていうのが、割合となる1割、2割っていう歩合や
25%、50%なんかの百分率っていうのが、いまいちわからないって人が
この割合のところで、つまずいたりしちゃうよね。
簡単に整理しておくと、こういうことだよ。
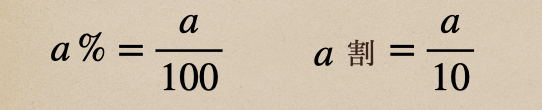
百分率(%)は全体を100とした時の割合で
歩合(割)ていうのが全体を10とした時の割合になるってことなんだね。
例えば、「\(x\)個の\(40\)%」のとき、式にしてみると
\(x×\frac{40}{100}=\frac{2}{5}x\)
ってことだね。
例題を解いてみよう。

りんごとぶどうの収穫量がいくつかってことを聞かれているので
りんごの収穫量:\(x\)個、ぶどうの収穫量:\(y\)個 としていくよ。
まずは、収穫量の合計\(350\)個って言っているので
\(x+y=350\)って等式がつくることができるね。
もう一つは、不良品の数の合計が\(60\)個ってことだよね。
りんごの不良品の個数はっていうと収穫量の\(20\)%ってことなので
\(x×\frac{20}{100}=\frac{1}{5}x\) になるね。
ぶどうの不良品の個数はっていうと収穫量の\(15\)%ってことなので
\(y×\frac{15}{100}=\frac{3}{20}y\) になるね。
なので、\(\frac{1}{5}x+\frac{3}{20}y=60\)の等式が成り立つよね。
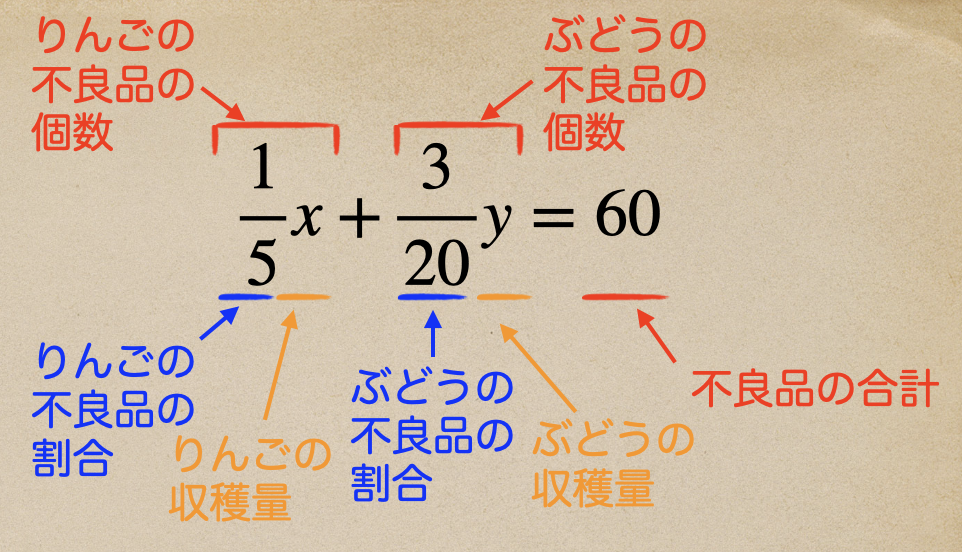
代金に関する問題の方でも解説したように
左辺、右辺が同じものになっている必要があって
この方程式は「個数+個数=個数」の等式になっているってことだね。
これで
\(x+y=350\)・・・①
\(\frac{1}{5}x+\frac{3}{20}y=60\)・・・②
っていう、連立方程式がつくれたってことだね。これを解いていくと…

ここでも、代金に関する問題と同じで、\(x=OO\)、\(y=OO\)で終わるのではなく
問いに対して、答えるようにして終わらせよう。
問いはりんごとぶどうの収穫量はいくつかってことなので
りんごの収穫量;150個、ぶどうの収穫量:200個としているってことだね。
□速さの問題
速さの問題ってなると、速さ、道のり、時間の3つの関係がポイントで
小学校でも、習ってきたそれぞれの関係式がこうだったよね。

この3つの内、2つが分かれば、残りの1つも関係式から
導き出せるってことだったよね。
これも、例題を解いてみよう。

この速さの問題っていうのは、文章だけで説明されていると
何を言っているのか、分かりにくいよね。
こういう時は絵に書いて状況を確認してみよう。
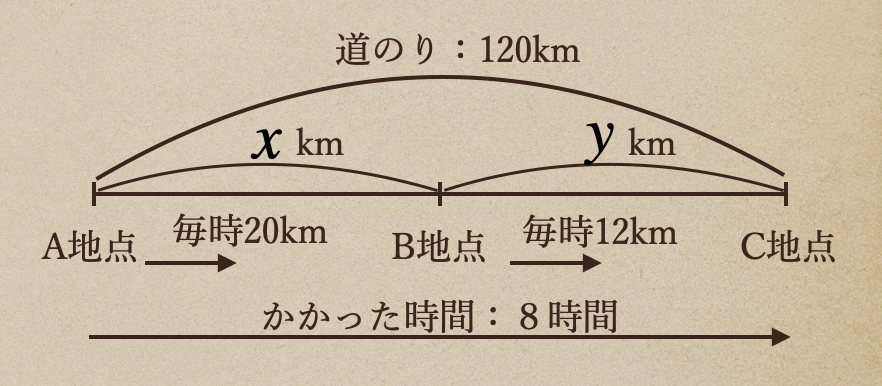
絵に書くとこうだね、問題ではA-Bの道のりとB-Cの道のりを聞かれているので
A-B間の道のりを\(x\)km、B-C間の道のりを\(y\)kmとして連立方程式をつくっていこう。
まずはA-C間の道のりは\(120\)kmってことなので、\(x+y=120\)になるよね。
そして、もう一つはA-C間までにかかった時間が\(8\)時間ってことなので
A-B間とB-C間それぞれでかかった時間が分かれば、方程式をつくることができるよね。
[時間]を求めようとすると、[道のり]÷[速さ]で求められるから
A-B間はっていうと、\(\frac{x}{20}\)となるよね。
B-C間はっていうと、\(\frac{y}{12}\)となるね。
これから、方程式は\(\frac{x}{20}+\frac{y}{12}=8\)で等式が成り立つよね。
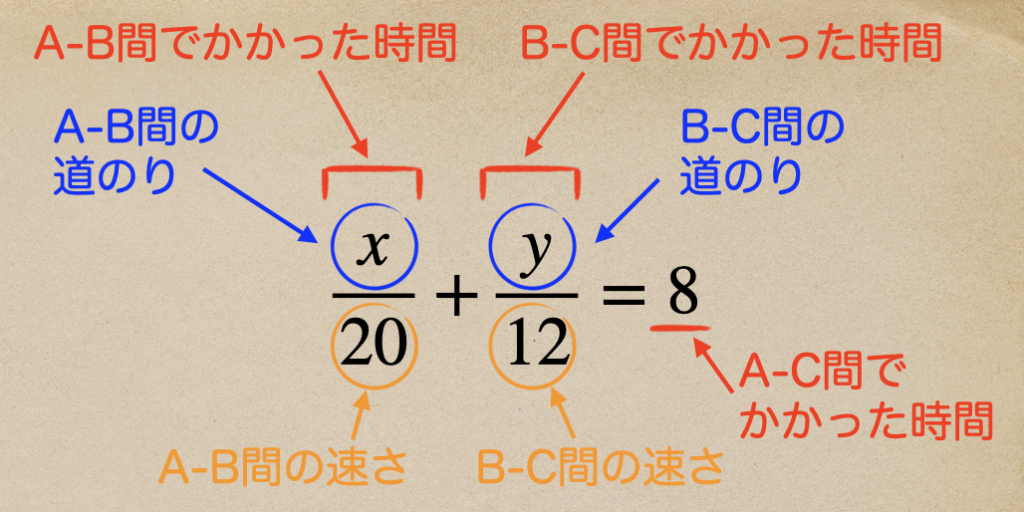
この等式は「時間+時間=時間」になっているってことだね
この、速さの問題で注意としては、3つの速さ、道のり、時間の
関係式で、いろいろな式をつくることができるんだけど
方程式をつくる中で、左辺と右辺の形が同じになっていないと
等式は成り立たないってことなので、方程式をつくる場合は
つくった式が何を表しているかっていうのを確認するようにしていこう。
2つの方程式がつくれたので、
\(x+y=120\)・・・①
\(\frac{x}{20}+\frac{y}{12}=8\)・・・②
の連立方程式をつくることができたよね。そして、これを解くと…
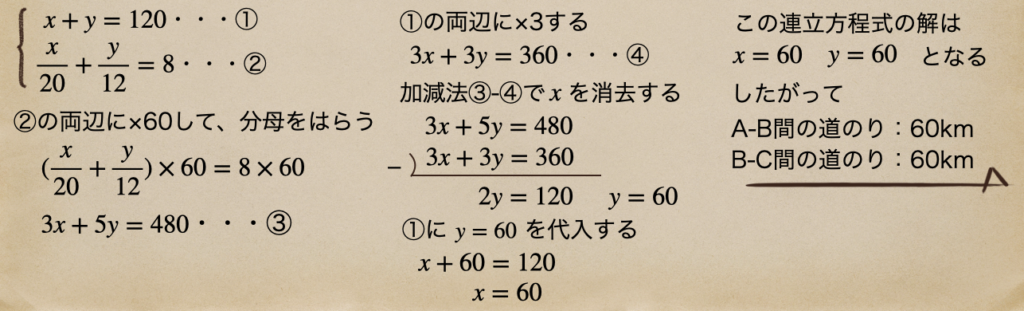
他の問題でも同じことが言えるんだけど、問題に出題されている値の単位には
十分、注意しておこう。
特に速さの問題では、[時間]は時間なのか、分なのか
[道のり]もkmなのか、mなのかをしっかり、確認しよう。
すべての単位があっていればいいんだけど、たまに、問題内では”m”として
出題されていて、答えのところで「何kmか答えよ」なんて
少し意地悪な、問題も出てくるかもしれないので、単位は必ず確認するようにしていこう。
以上が連立方程式になります。
結構、長めの内容になっちゃったけど、一つ一つ、かなり重要なものに
なっているので、一つ一つをしっかり理解できたってなってから
次の項目に進むようにしていってくだい。
ここまでの記事が良かったと思ったらここをクリックしてね。
質問なんかがあった場合はコメントにお願いします。
では、またさようなら。



コメント