どうも、こんにちはDKです。
今回は正の数・負の数の計算について学んでいこう。
このブログでの内容は動画でも解説してるよ。
※動画再生は音が出るから注意してね。
ちなみに、計算には加法、減法、乗法、除法の4つがあってこれらをまとめて四則(しそく)と
呼ぶんだ。それぞれ、
加法(かほう):足すこと・・・+ その答えを『和(わ)』と呼ぶ
減法(げんぽう):引くこと・・・ー その答えを『差(さ)』と呼ぶ
乗法(じょうほう):かけること・・・× その答えを『積(せき)』と呼ぶ
除法(じょほう):割ること・・・÷ その答えを『商(しょう)』と呼ぶ
ってこと。言葉とどう言う計算のことかは理解しておこうね。
これから数学を行なっていく上で、最終的に行き着くのが
四則の計算になってくるから、基礎を理解して、数をこなして慣れていくことが大事になってくるよ。
じゃあ、早速やっていこう。
正の数・負の数の加法
加法、減法は小学生で学んだ、加法(かほう)ってのは”足すこと”だね。
ただ、中学では正の数だけでなく、負の数の”足す”をするため
少しややこしくなっちゃうんだね。
加法の場合
4+6 は 4より6大きい数 を求めることになるよね
同様に、
(ー4)+6 は −4より6大きい数 を求めることを言うんだね。
それぞれを数直線上で書き表すと⇩こうなるね。

だから、それぞれの答えは
4+6=10 (ー4)+6=2
となることがわかったね。これは正の数を足した場合の考え方になるんだ。
次は負の数を足した場合どうなるか考えてみよう。
4+(ー6) は 4より−6大きい数を求めるんだよ。
(ー4)+(ー6) は ー4より−6大きい数を求めるってことになるんだね。
それぞれを数直線上で書き表すと⇩こうなるね。
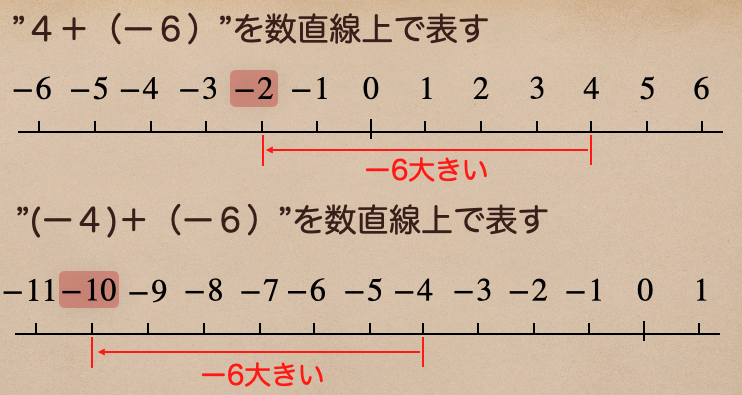
それぞれの答えは
4+(ー6)=ー2 (ー4)+(ー6)=ー10
ってなるんだね。
加法(足し算)するだけなのに、ややこしいよね。
加法に対してのポイントを教えるね。
正の数・負の数の加法
①同符号の2つの数の場合の和
符号は2つの数と同じ符号にする
絶対値は2つの絶対値の和
②異符号の2つの数の場合の和
符号は絶対値の大きい方の符号をつける
絶対値は2つの数の大きい方から
小さい方を引いた数

2つの数が同符号か異符号かによって計算のやり方が変わっちゃうけど
初めのうちはこのやり方で慣れていこうね。
加法には計算法則っていうのがあって、これも覚えておこうね。
加法の交換法則・・a + b = b + a
例:4+6=6+4、(ー4)+6=6+(ー4)
加法の結合法則・・( a +b ) + c = a + (b + c )
例:(4+6)+5=4+(6+5)
それぞれの法則はむずかしそうに見えるけど、単純に加法(足し算)の式であれば
並び替えて計算しても、どこから計算してもいいよってことだね。
ただ、気をつけておくべきなのは、式が全て、加法になっている必要があるよ。
次は減法について学んでいこうね。
正の数・負の数の減法
減法では、2パターンあることを知ってそれぞれのパターンでどのような計算になるかを
理解していこうね。
①正の数を引く
例えば、(+4)ー(+6)や(ー4)ー(+6)のような式だね。
(+4)ー(+6)の場合、+4より+6小さい数を求める計算だよね。
これは言い換えると +4より−6大きい数を求める計算と同じことが言えるんだね。
これって、加法でも同じ言い方していたの覚えてる?
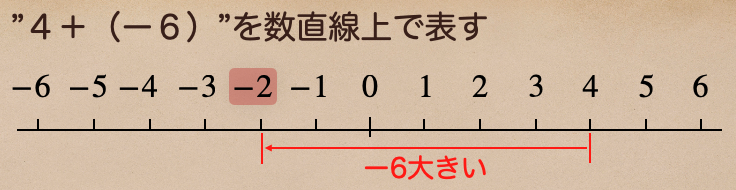
そうだよね、4+(ー6)の時と同じだよね。ようするに、
(+4)ー(+6)=(+4)+(ー6)=−2 と同じことになるんだね。
同様に(ー4)ー(+6)の場合、−4より6小さい数を求める計算だよね。
これも言い換えると −4よりー6大きい数を求める計算と同じことが言えるんだ。
これも、加法でも同じ言い方していたよね。

(ー4)+(ー6)と同じ計算になるよね。ようするに、
(−4)ー(+6)=(ー4)+(ー6)=−10と同じになることがわかったね。
次のパターンも見てみよう。
②負の数を引く
例えば (+4)ー(ー6) (ー4)ー(ー6)のような式だね。
(+4)ー(ー6)の場合、 +4より−6小さい数の計算だよね
これも、言い換えると +4より6大きい数の計算となるんだ。
あれっ、これって単純に4より6大きいってことだよね。
そうすると、 (+4)ー(ー6)=(+4)+(+6)=10 となるね。
同様に(ー4)ー(ー6)の場合、 ー4より−6小さい数の計算になるよね。
これも、言い換えると ー4より6大きい数の計算となるね。
ようするに (ー4)ー(ー6)=(ー4)+(+6)=2 となるね。
ここで、減法のまとめだよ

減法の場合、結果として、引き算が足し算になっただけと思ったよね。
そのとおりなんだ、減法はまず加法に変えることが大事なんだね、これは何でかって言うと
次の加法と減法の混じった計算で必要になるからなんだ。
加法と減法の混合計算
加法と減法が混ざった計算式については学ぶというよりは計算式そのものをいかに簡単にして解くかが重要になってくるよ。
なぜ簡単にするかって?それは、簡単に計算できる方が、間違いが少なくて済むからなんだ。
数学って言うのは、いかに計算を簡単にして、間違うことなく早く解けるかが大切になるんだ。
だから、どうやったら簡単にできるかを考えながら解いていこうね。
例えば、 (+7)ー(+5)+(ー8)ー(ー3) って式があったとするね。
これを普通に解いた場合、左から順に解いていく?それとも式を簡単にしてから解いていく?
試しに左から順に解いていくね。

今回の例題はさほど、難しくないので左から順に解いても間違いは少ないかもしれないけど
正の数、負の数を加法、減法していくと、符号が換えたり、加法を減法にしたりしながら解くのは
相当な慣れが必要になってくるんだ。だから、上の例題の場合はまず…

この計算だと、減法がすべて加法に変えて、さらには正の数と負の数をそれぞれ計算して最後に
残りを計算することができるから、間違いが少なくできるよ。
慣れてくれば、②の順番を変えるなんかは飛ばして、計算してしまってもオッケーだよ。
また、加法だけの式で正の数の和、負の数の和で計算した+7、+3、ー5、ー8を項(こう)と言うんだ。その中でも+7、+3を正の項、−5、ー8を負の項と呼ぶからここも覚えておこうね。
中学校からの数学は問題に対して、どのように解いたかが採点の一部になってくるんだ。
だから、問題と答えだけ記入して正解していても減点されてしまうからしっかりと
どのように解いたかまでを書く癖をつけようね。言葉で説明する必要はないよ。

解き方の途中で、式が間違えている、計算が間違えている場合は減点となることもあるから
計算式を書く時には、間違いのないように解こうね。
次は正の数、負の数の乗法、除法を学ぶね。
ここまでの記事が良かったと思ったらここをクリックしてね。
コメントもくれるとうれしいな。





コメント