どうも、こんにちはDKです。
ここでは、中学生で習う数学の基礎を解説しているよ。
今回は中学2年生で習う、確率の続きやっていきますね。
確率って何?や確率の求め方っていうのは、「中2-6(1).確率と場合の数」の方で
解説しているので、確率についてもっと学びたいって人は、そっちも
みてみてください。
今回は、いろいろな確率として問題でよく使われるものを紹介しておくね。
それぞれで場合の数の考え方も見ていこう。
動画でも、基礎の解説やっているんで、よかったらそっちも見てみてください
(注:音が出るよ)
(1)サイコロの確率
サイコロを投げて出た目の確率を求めるっていうのがよく使われて
2個のサイコロを投げる場合なんかもあるね。
このサイコロっていうのは、1から6までの目があるので
1個のサイコロで起こり得る場合の数っていうのは”6通り”ってことになるね。
これが2個使った場合だと”6×6通り”、3個だと”6×6×6通り”って考えていくようにしよう。

(2)コインの確率
これは表・裏のでかたを問われる問題になりますね。
コインを投げる確率の場合、複数のコインを投げて
その時の表と裏の組み合わせを確率で求めるって問題があるね
コインの表裏のすべての場合の数は、2通りで、コインの枚数分だけ
×2をしてあげればすべての場合の数を求めることができるね。
あることがらの起こる回数は、樹形図にしてみてあげるのがいいね。

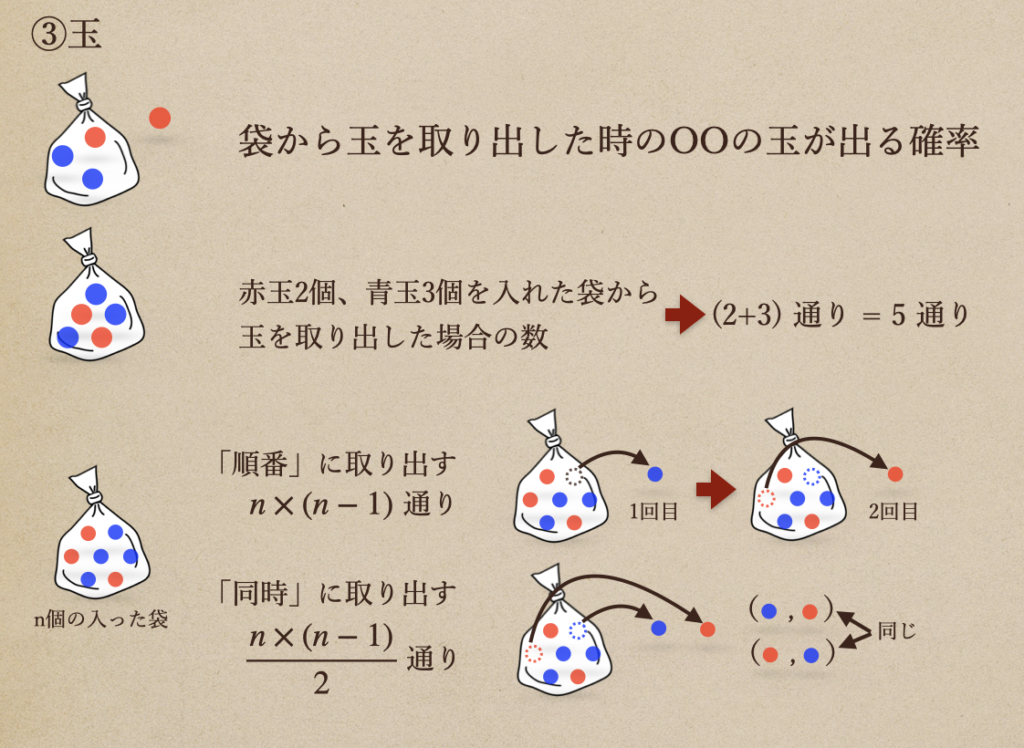
(3)玉を取り出す時の確率
2色以上の玉を取り出してその時のあることがらの起こる確率を求めたりするんだね。
袋から玉を取り出す場合のすべての場合の数は、袋に入れている玉の数によるね。
赤玉2個、青玉3個を入れた袋の場合、すべての場合の数は5となるってことだね。
あと、袋から玉を取り出す時っていうのは、「順番」に取り出す場合と「同時」に取り出す場合
があって、それぞれの取り出し方によって、すべての場合の数っていうのは変わってくるんだね。
n 個の玉が入っている袋があったとして。。
・「順番」に取り出したときの場合の数は \(n×(n-1)\) 通り
・「同時」に取り出したときの場合の数は \(\frac{n×(n-1)}{2}\) 通り
になるんだね。
「順番」の場合、取り出した玉が1回目、青で2回目、赤だったとき
(青、赤)の組み合わせになるんだけど、「同時」の場合だと一緒に2個取り出すことになるので
その時に取り出した玉が(青、赤)であった場合、(青、赤)(赤、青)の並びは関係ないことに
なるんだね、だから、取り出したときの場合の数っていうのを半分(\(\frac{1}{2}\))に
してるってことなんだね。
ただ、上の場合の数は袋から2回取り出したときなので
3回「順番」に取り出したときの場合の数っていうのは \(n×(n-1)×(n-2)\) 通り
となるので、ここは注意しておこう。
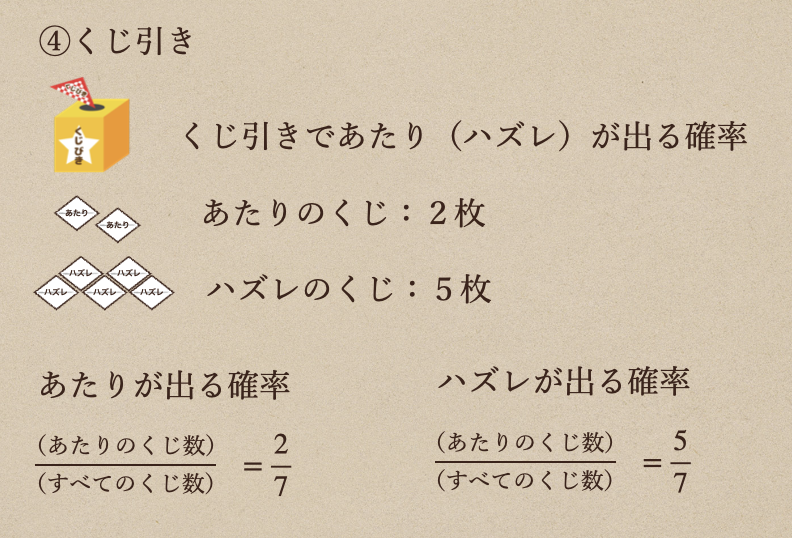
(4)くじ引きの確率
くじ引きの場合は、あたりの本数、ハズレの本数が分かれば
確率を求めていくことができるね。
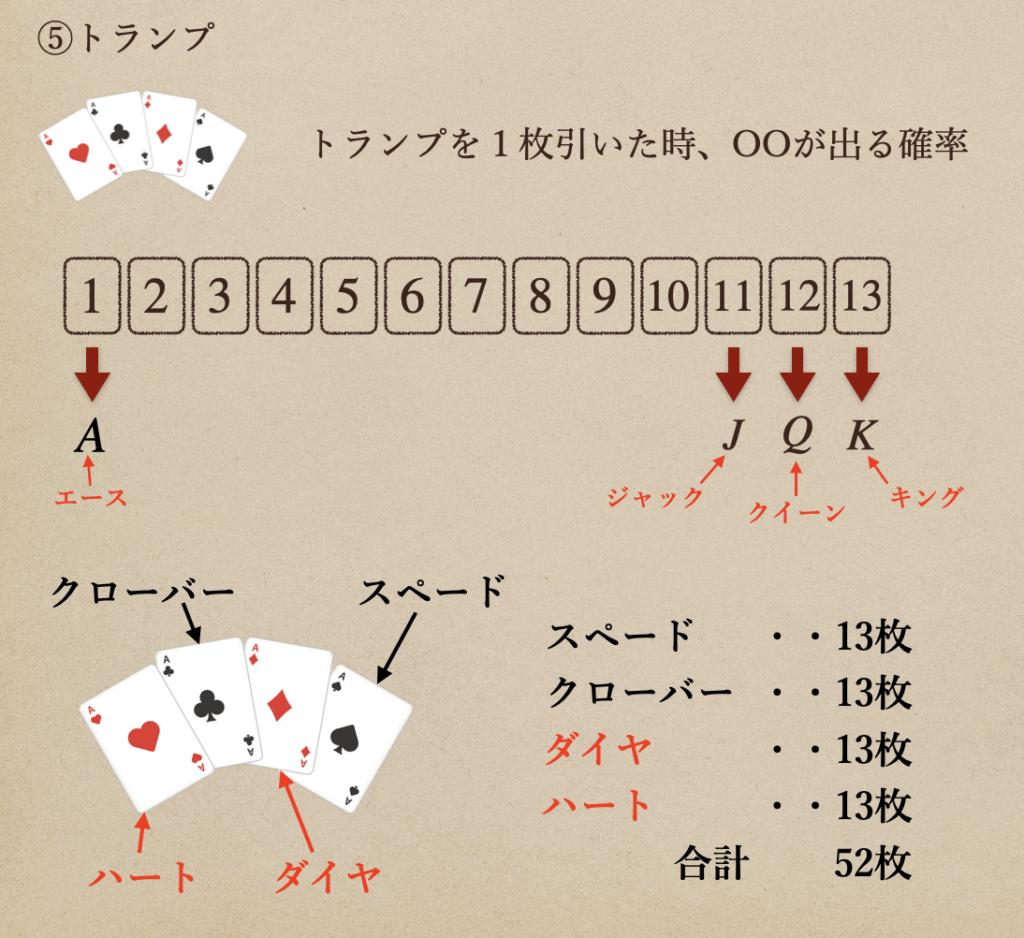
(5)トランプの確率
トランプは枚数が多く、これの確率っていうのを考えるとややこしそうって
思うかもしれないんだけど、トランプっていうのは特徴があってそれを
覚えておくことで、簡単に確率は求めることができるようになるので
その特徴を覚えておこう
[特徴1]
トランプの数字は1から13まであって、そのうち「1」,「11」,「12」,「13」は
アルファベットで表示される。
「1」 ・・・「A」 ※エースと言う
「11」・・・「J」 ※ジャックと言う
「12」・・・「Q」 ※クイーンと言う
「13」・・・「K」 ※キングと言う
[特徴2]
トランプは4つのマークがあり、マークには2色の色分けがある
♠️:スペード (黒色)
♣️:クローバー (黒色)
♦️:ダイヤ (赤色)
❤︎:ハート (赤色)
[特徴3]
トランプの枚数はマーク4種×数字(1〜13)=52枚ある
ここにあげた、パターンのそれぞれの考え方っていうのを
しっかり理解しておいてもらえると、関連する確率の問題も求めやすくなるよ。
あとは、いろいろな確率の問題を解いてみて確率の求め方に慣れていくようにして行ってみてくだい。
今回は、ここまでになります。
ここまでの記事が良かったと思ったらここをクリックしてね。
質問なんかがあった場合はコメントにお願いします。
では、またさようなら



コメント