どうも、こんにちは DK です。
ここでは、中学生で習う数学の基礎を解説しています。
今回は、中学2年生で習う、データ比較と箱ひげ図についてやっていきますね。
中学1年生ではデータの活用ってところで、度数分布やヒストグラムっていうのを
習ってきたと思うんだけど、それらは、1つのデータの傾向や特徴っていうのを
見るときに使われるものになるんだね。
ここでは、複数のデータの分布の様子や比較する方法についての学びを解説していきますね。
動画でも、解説しているのでそちらも見てみてください。(注)音が出るよ
四分位数と四分位範囲
いきなり、聞きなれない言葉が出てきたんだけど、例を挙げながら解説していくね。
まずは、1年生と2年生の1週間の自宅での学習時間の集計をとったデータがあったとするね。

データをただ集めただけだと、1年生と2年生でどんな違いがあるのかっていうのがわかりにくいよね。
それに、1年生は14人分、2年生は13人分の集めたデータとなっているんだね。
こんな時のデータの傾向を分析するのに有効なのが、大きい順に並べて4等分して
分布の様子を調べる方法があるんだね。
この4等分するときの位置にある値っていうのを四分位数(しぶんいすう)って言うんだね。
実際にさっきの学習時間を4等分してみるね。

この青点線で引いた場所っていうのが、それぞれ四分位数ってことになるんだね。
そして、この四分位数って言うのは、小さい方から順に
第1四分位数、第2四分位数、第3四分位数と言って、第2四分位数って言うのは
データの中央値になっているんだね。
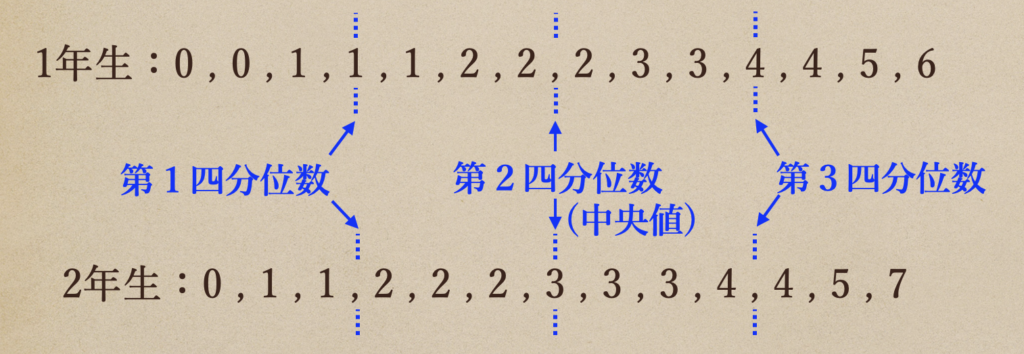
けど、データの数によっては、四分位数が数字と数字の間になっているところがあるよね
その場合は、前後2つの数字の平均値っていうのがそれぞれの四分位数になるってことだね。
なので、
第1四分位数は1年生は「1」、2年生は「1.5」
第2四分位数は1年生は「2」、2年生は「3」
第3四分位数は1年生は「4」、2年生は「4」
ってことになるんだね。
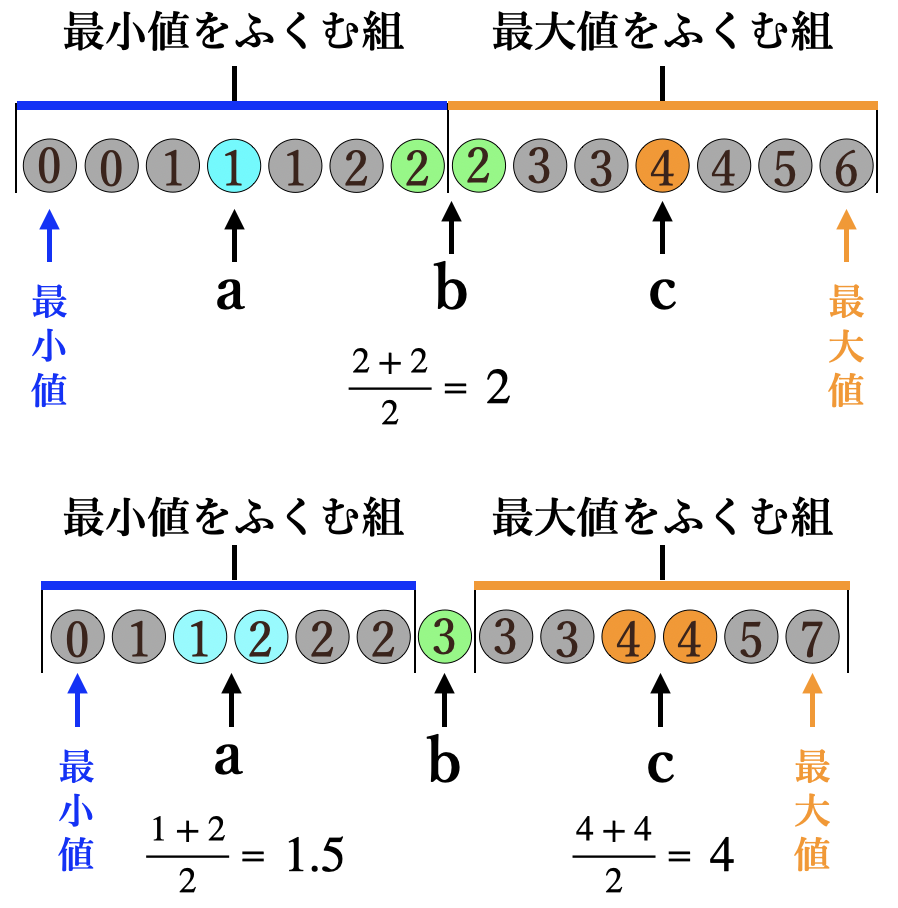
ここで、四分位数の求め方っていうのをデータが奇数と偶数の場合で
見比べながら確認しておきますね。
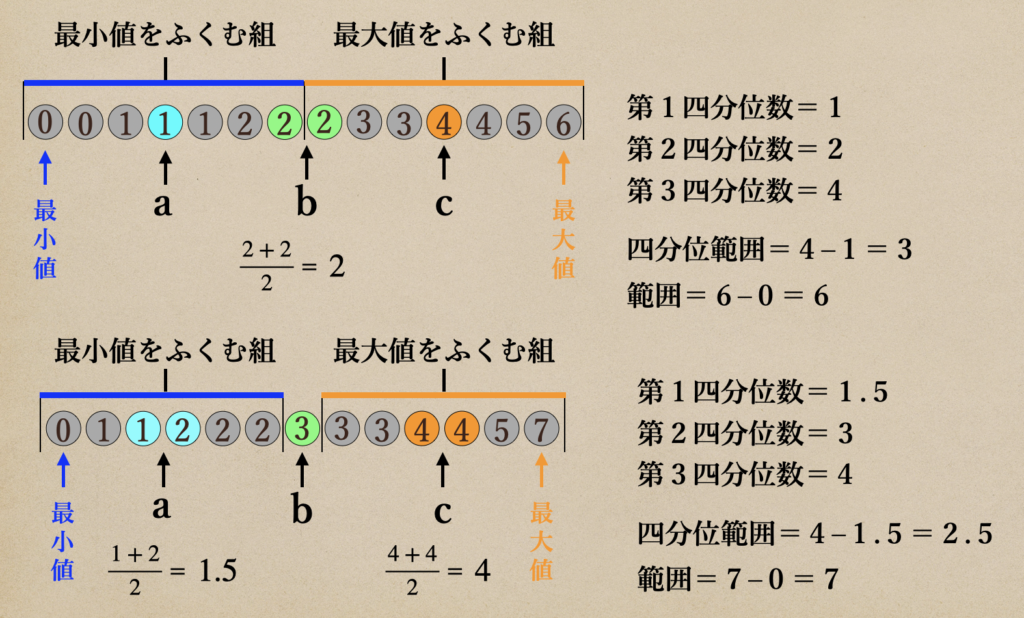
【四分位数の求め方】
①データの小さい順に並べて
中央値 b (第2四分位数)を求める
②中央値を境にして、最小値をふくむ組
最大値をふくむ組に分ける
③最小値をふくむ組の中央値 a
(第1四分位数)を求める
④最大値をふくむ組の中央値 c
(第3四分位数)を求める
データの数が偶数の場合は中央値が2つになるので、その平均値になるんだね。
データの数が奇数の場合は中央値は1つになるんだけど、最小値をふくむ組と
最大値をふくむ組は中央値を除く必要があるので、ここは注意が必要だね。
そして、データが奇数の場合は、最小値をふくむ組と最大値をふくむ組は
偶数になるので、それぞれの中央値である第1四分位数と第3四分位数は
2つの値の平均値で求めてあげるんだね。
あと、第3四分位数と第1四分位数の差っていうのを四分位範囲(しぶんいはんい)って
言うっていうのも覚えておこう。
ちなみに、最大値と最小値の差は「範囲」って言い方になるよ。
【四分位範囲(しぶんいはんい)】
(第3四分位数)ー(第1四分位数)=(四分位範囲)
【範囲】
(最大値)ー(最小値)=(範囲)
なので、1年生のデータの場合 四分位範囲は4−1=3となって範囲は6−0=6ってことだね。
2年生のデータの場合 四分位範囲は4ー1.5=2.5となって範囲は7−0=7となるんだね。
これらをまとめると。。
こんな風に、四分位数を求めることができるんだね。
この四分位数を求めてみたけど、この数字だけ見てもデータの傾向を分析するには
まだ、わかりにくいよね。次はこの四分位数を使って箱ひげ図っていうのをかいてみるね。
箱ひげ図
箱ひげ図(はこひげず)は1年生の1週間の自宅学習時間を元に書いてみましょう。
一つ前のところで四分位数は値はそれぞれ求めてわかっていましたよね。
それを表にしてまとめると。。

これを、箱ひげ図にしてかくと、こんな風にかくことができるんだね。
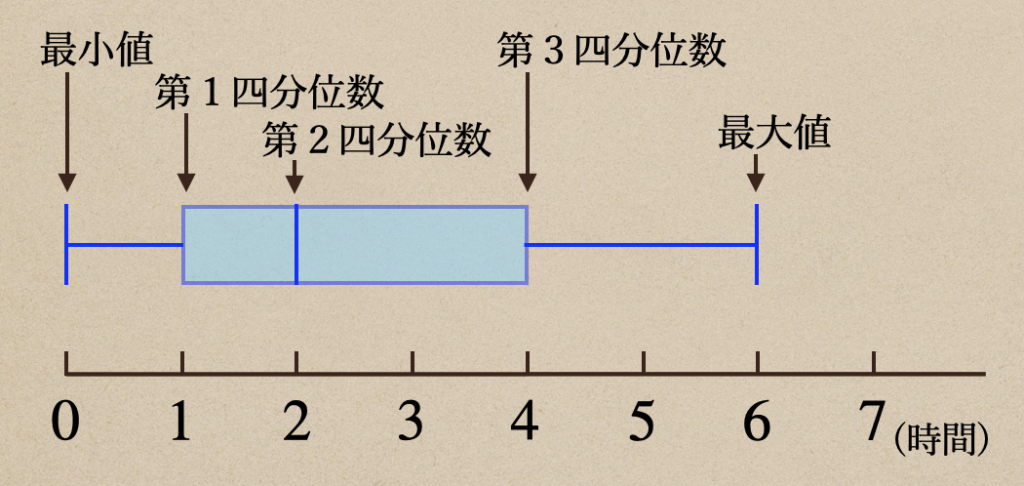
これが箱ひげ図ってことになるんだね。
かき方としては、
①最大値、最小値に縦線を引く
②第1四分位数から第3四分位数を四角形でかく
③第2四分位数に縦線を引く
④四分位数の四角形以外のところを最大値、最小値に横線を引く
となるね。ちなみに、四分位数の四角形を塗りつぶす必要はないからね。
それと、この箱ひげ図で四分位範囲と範囲がどこになるのかって言うと
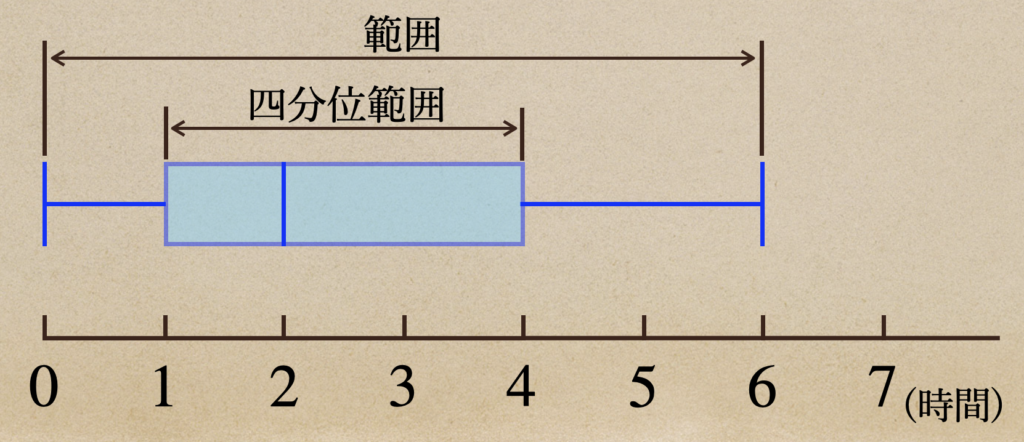
この部分を言っているってことをになるんだね。
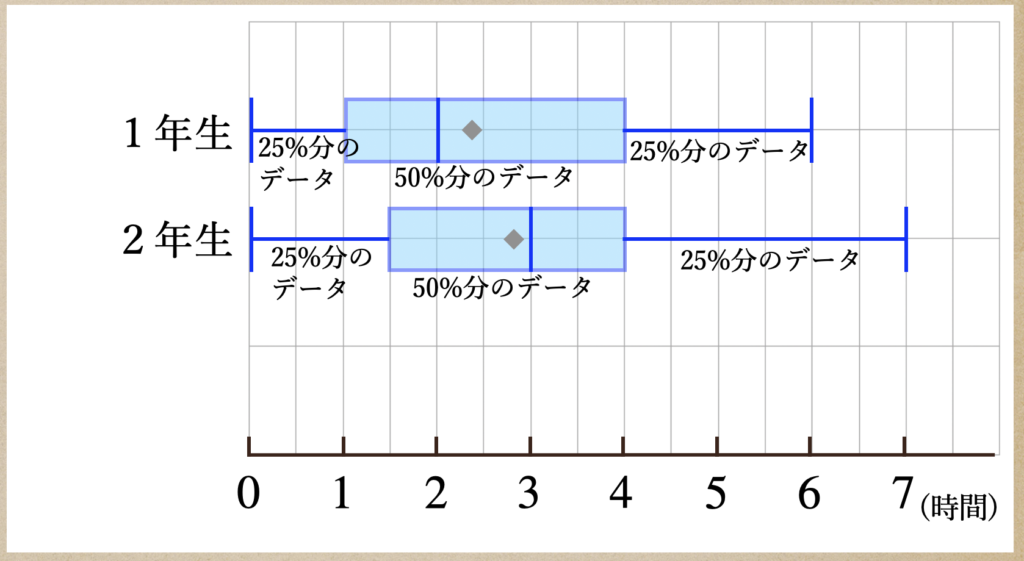
箱ひげ図を使って、1年生と2年生を比較してみると

こんな風になるんだね。図の中の◆はデータの平均値を書き込んでみたよ。
平均値と中央値は違うってことを理解しておこう。
この箱ひげ図の特徴としては、1年生は14人のデータで2年生は13人のデータから
箱ひげ図をかいているんだけど、ひげの長さって言うのはデータの値(最大値、最小値)によるので
ひげの長さが長いからデータが多いとは限らないってことなんだね。
あと、箱ひげ図の四分位範囲って言うのは、データの50%、ようするに半分がこの中に
含まれていて、最小値側、最大値側っていうのがそれぞれ25%のデータになるってことなんだね。
この特徴を理解した上で、この箱ひげ図は複数のデータの分布の様子を
比較することができるんだね。
ヒストグラムと箱ひげ図
ヒストグラムと箱ひげ図の関係をやる前に
箱ひげ図を見るときのポイントを確認しておきますね。
例えば、「25回の計測を行った結果」の箱ひげ図がここにあったとするね。
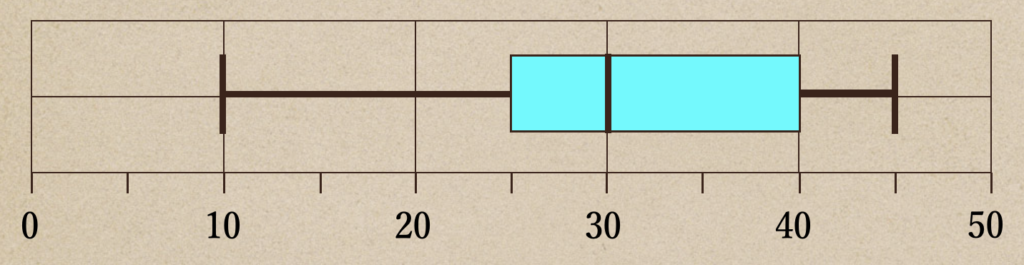
この箱ひげ図からわかることって言うのを見ていくと
最小値、最大値、第1四分位数、第2四分位数、第3四分位数がわかるよね。
そして、この5つがデータのどの部分かって言うのも、データの個数がわかっていれば
わかるよね。
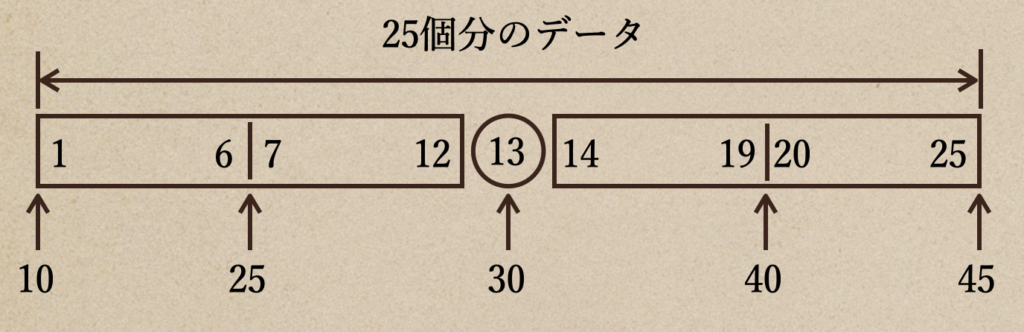
今回のデータは25個なので、中心値となる第2四分位数はデータの
小さい方から13個目ってことで、これが30ってことがわかるよね。
同じように見ていくと、第1四分位数は6番目と7番目の平均値で25となって
第3四分位数は19番目と20番目の平均値で40ってことだね。
箱ひげ図でわかることって言うのは、上の図のように、全体のデータ個数に対して
それぞれの四分位数の位置とそのときのデータの値になるんだね。
これをしっかり理解しておくようにしよう。
あと、この箱ひげ図っていうのは、ヒストグラムと合わせることでデータの分布の様子を
よりくわしく見ることもできるんだね。
今度は、データ①から④までの内容が次のような場合で見ていきますね。
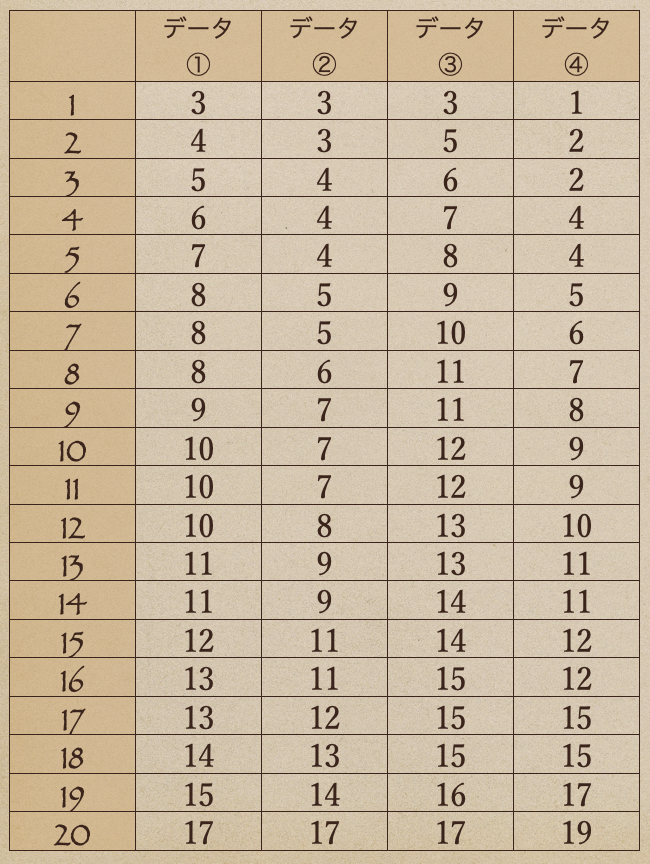
このデータから、度数分布表と四分位数を表にすると。。
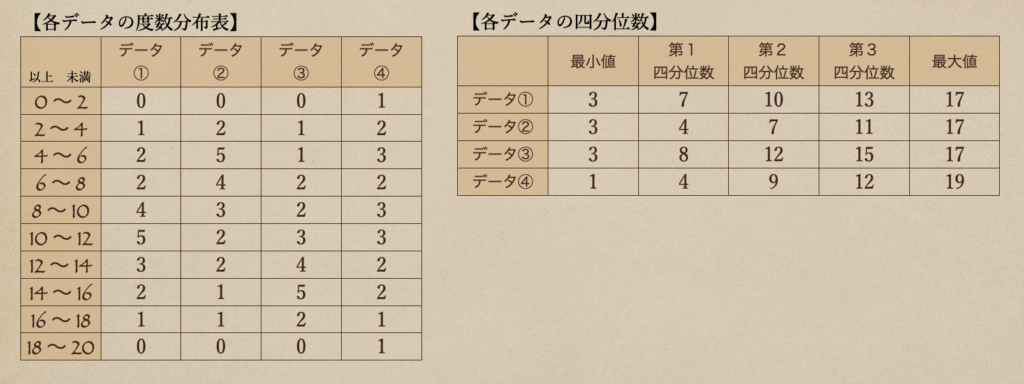
こんな風にまとめることができるんだね。
この表はみんなも自分で作ってみて、確認してみてね。
これらの表から、ヒストグラムと箱ひげ図をかいて見ると。。
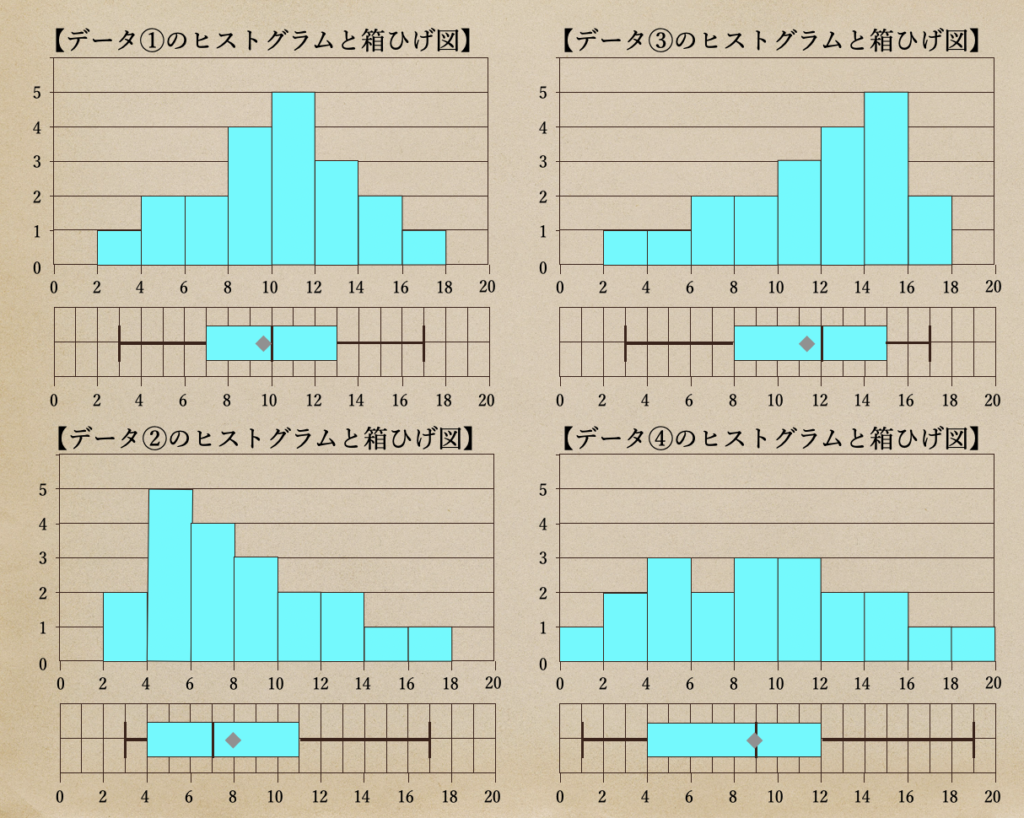
こんな風にかくことができるんだね。
ここで、ヒストグラムと箱ひげ図にどんな傾向があるのかっていうのを確認してみよう。
【ヒストグラムと箱ひげ図の関係】
(1)四分位範囲はヒストグラムの山が大きいところにかたよる
(2)中心線はヒストグラムの高い山よりに位置している
(3)箱ひげ図の最大値、最小値の範囲はヒストグラムの両端の山と同じ
この関係っていうのは、データの個数、図の書き方によっては、見え方っていうのが
変わってきたりするんだけど、関係性としては同じことが言えることになるんだね。
ヒストグラムと箱ひげ図の関係っていうのは、問題でも度々、出題されることがあるので
しっかり理解しておいてください。
今回は、ここまでになります。
ここまでの記事が良かったと思ったらここをクリックしてね。
質問なんかがあった場合はコメントにお願いします。
では、またさようなら。



コメント