どうもこんにちは、DKです。
今回から、中学3年生の単元に入っていきますね。
最初は「多項式」からですね。多項式って聞くと1年生や2年生で
習ったところって思うかもしれないんだけど。
この3年生の多項式っていうのは、多項式同士の乗法になっていて
計算のややこしさが、数段アップしているものになるんだね。
それと、3年生から習うことっていうのは、ある意味、数学らしくなってくるので
難しさもアップしているんだね。
なので、ここで基礎をしっかり学んで、しっかり理解をしていってください。
では、さっそく基礎の解説、始めていきますね。
1.多項式と単項式の乗法、除法
まずは、2年生でも少し、習ってきた単項式、多項式について軽くおさらいしておこう
単項式:項が一つだけの式
多項式:項が2つ以上ある式
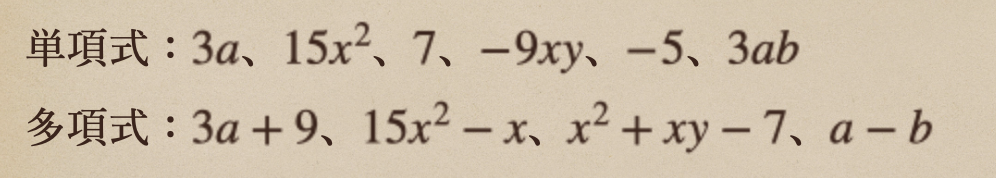
簡単に言うと、こう言うことだったよね。
この章では、単項式と多項式の乗法について、見ていきますね。
単項式と多項式の情報っていうのは、2年生で習った数の項と多項式の乗法と
同じで、分配法則を使って計算してあげるってことなんだね。
\(a(b+c)=ab+ac\)
\((a+b)c=ac+bc\)
こんな風に、カッコの外の単項式をカッコの内のそれぞれにかけて
計算してあげるってことになるんだね。

細かく解くとこんな感じになるんだね。
実際、ここまで細かく書く必要もないけど、すぐに計算間違いをしてしまうって
人は、一つずつていねいに解いていくことから始めてみよう。
単項式と多項式の除法は、これも多項式と数の項の除法と同じように
式を分数の形で表して簡単にするか、除法を乗法に直してから計算するかの
2通りの解き方があるね。
\((a+b)÷c=\frac{a+b}{c}\)
\((a+b)÷c=(a+b)×\frac{1}{c}=\frac{a}{c}+\frac{b}{c}\)
除法はどちらの方法で解いても、解は同じになるよ。
ただ、分数の形にする方法で注意が必要なのは、分母は分子の多項式のどちらにも
かかっているってことなんだね。
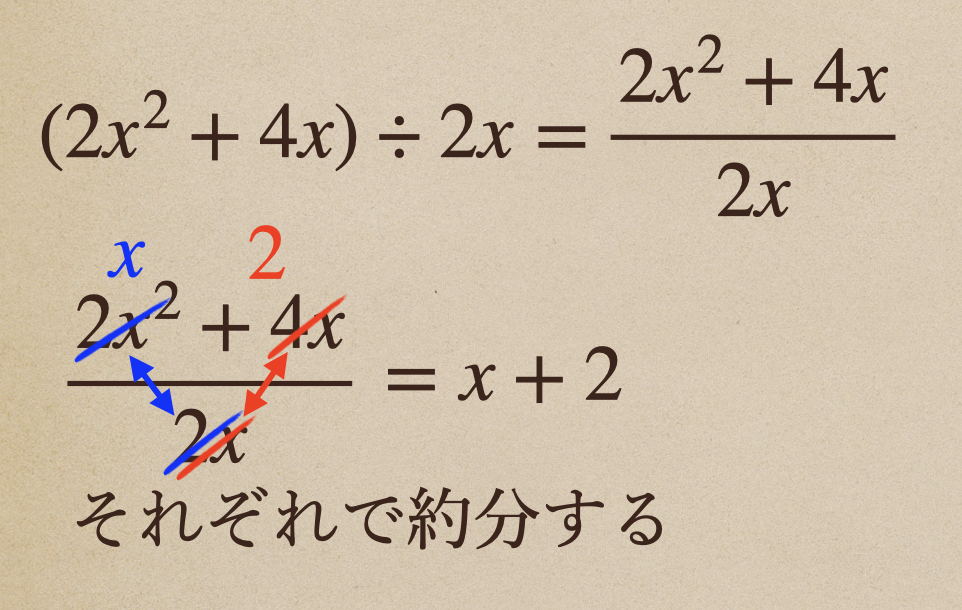

考え方としては、分子の多項式でお互いが割れる単項式でカッコを作ってあげると
カッコの外に出ている項と分母の項で約分してあげるといいってことだね。
初めのうちは、約分するのが難しく感じるかもしれないんだけど慣れてくれば
自然に解き方を身につけていけると思うので、いろんな問題を解いて
解き方に慣れていくようにしていこう。
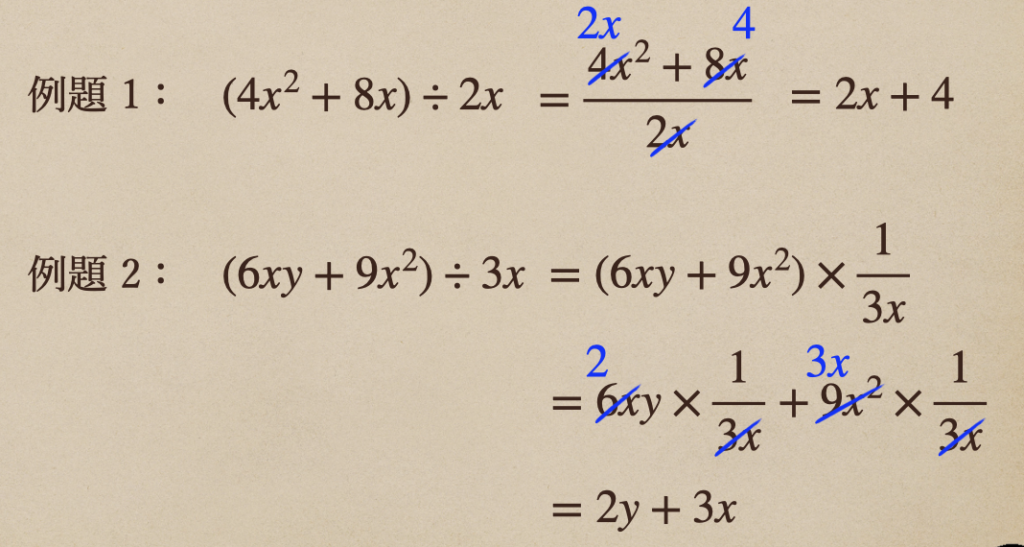
例題で解いてみると、こんな感じだね。
約分する時に、間違えやすいので注意しておこう。
2.多項式の乗法
まずは、これを見てみて。
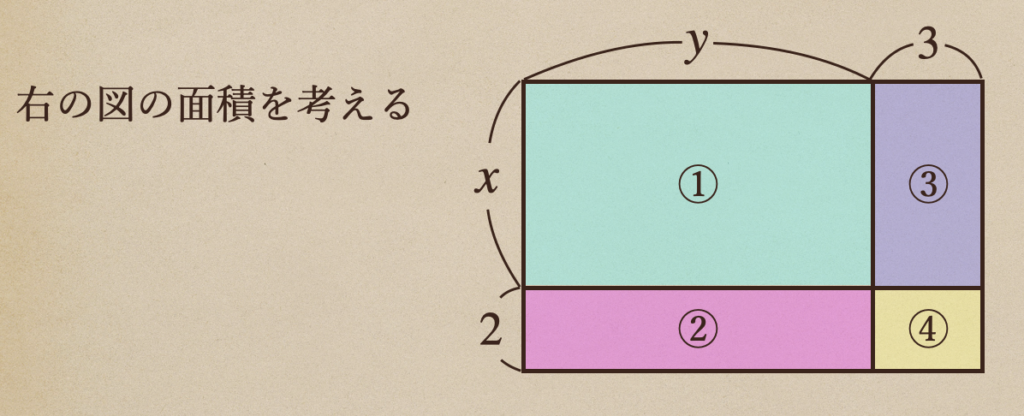
四角形があって、その中に横線と縦線を引いて、4つの四角形ができているよね。
このそれぞれの面積を見てみると。。
[①の面積]\(x×y=xy\)
[②の面積]\(2×y=2y\)
[③の面積]\(x×3=3x\)
[④の面積]\(2×3=6\)
全体の面積は、①+②+③+④=\(xy+2y+3x+6\)・・・⑤
ってことになるよね。図からタテの長さは\(x+2\)、ヨコの長さは\(y+3\)となるよね。
ようするに全体の四角形の面積は\((x+2)(y+3)\)・・・⑥ として表すことができるんだね。
そして、⑤で表した式と⑥で表した式っていうのは、同じ四角形の面積ってことで
⑤ = ⑥ってことで、\((x+2)(y+3)=xy+2y+3x+6\)となるってことだね。
他にも、多項式を計算する時の考え方として次のように考えることもできるよ。
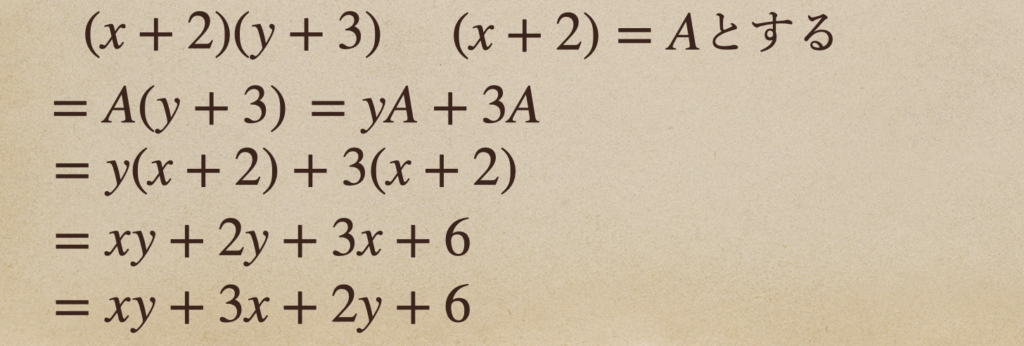
どちらかの多項式を単項式に置き換えて計算することで
それぞれをかけることで求めることができたね。
こんな風にカッコを外して計算することを「展開する(てんかいする)」っていう
言い方をするんだね。展開するっていうのはこういうことだね。
<展開する>
単項式と多項式の積や多項式と多項式の積の形をした式を1つの多項式に表すこと
多項式と多項式の積で\((x+a)(y+b)\)を展開すると
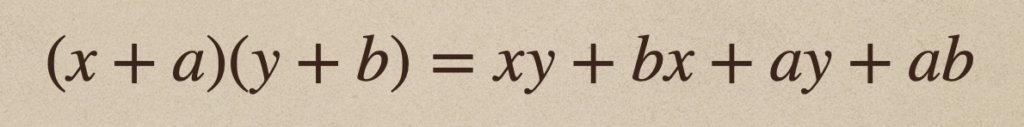
この展開のされ方っていうのは、これからもよく使われるのしっかり覚えておこう。
公式っていうわけじゃないのでわざわざ覚える必要なくて、多項式と多項式の積は
それぞれかけてあげて展開してあげてるだけなので、展開する方法っていうのを
しっかり理解しておこう。
覚えておく必要があるのは次に解説する「展開の公式」でこれは大事な公式なので
しっかり、理解して覚えていくようにしていってくださいね。
今回は、ここまでになります。
ここまでの記事が良かったと思ったらここをクリックしてね。
質問なんかがあった場合はコメントにお願いします。
では、またさようなら。



コメント