どうもこんにちは、DKです。
このブログでは中学数学の基礎を学びたい人向けに
各単元の基礎の解説を行っています。
今回は中学3年生で習う多項式の展開の公式についてやっています。
多項式は4回に分けてるので他のブログを見たい人は こちら から
アクセスしてみてください。
式の利用
ここまでに解説を行ってきた、展開の公式や因数分解っていうのがいろいろな場面で
役に立てることができるんだね。
(1)展開の公式(乗法公式)の利用
ここに文字式ではない、数字 \(51^2\) っていうのがあったとして
これを計算しなさいってなった場合、みんなはどうやって計算をするかな?
普通に計算をして、\(51^2=51×51=2061\)ってするよね。
けど、これを展開の公式っていうのを使って計算してあげることができるんだね。
それが、\(51^2=(50+1)^2\) として考えてあげるんだね。
この\((50+1)^2\)っていうのは、\((x+a)^2\)と同じ形になってるんだね。
ようするに展開の公式の \((x+a)^2=x^2+2ax+a^2\) を利用して計算してあげることが
できるんだね。
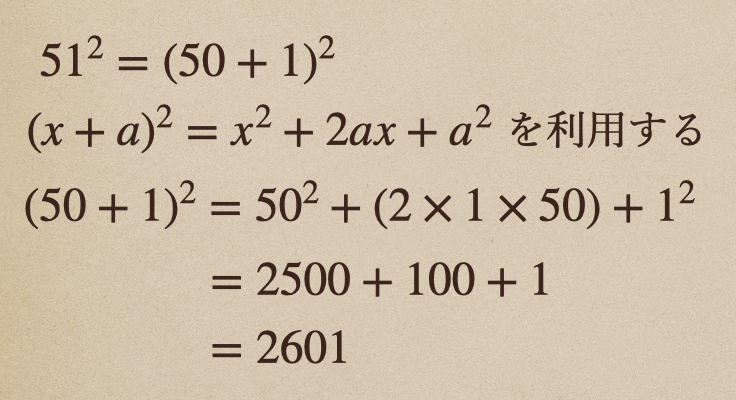
展開の公式を使って、解いてあげると、計算がしやすくなって
暗算でも計算することができたよね。
もう一つ、例題を考えてみよう。
例題 \(48^2\)
これを展開の公式を利用して計算してみるね。
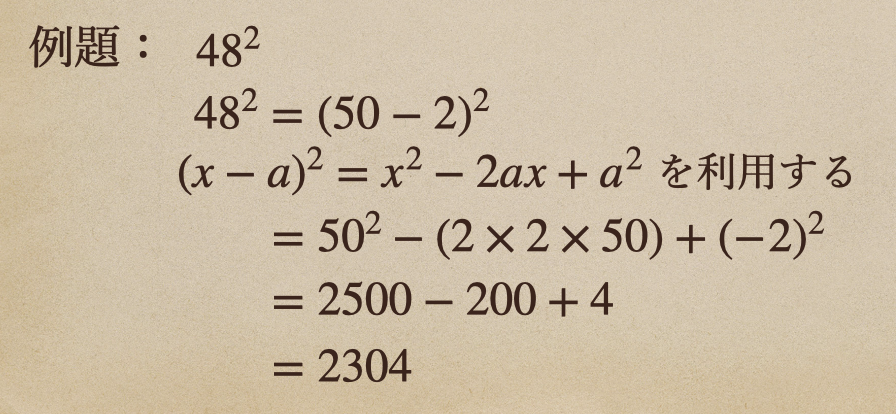
キリのいい数字にしやすかったりした場合には有効な計算方法なので
考え方っていうのを理解して、活用してみよう。
(2)因数分解の公式の利用
今度は、因数分解の公式を使った計算方法だね。
これも、(1) と同じで文字数を使わない計算式\(65^2-35^2\)っていうのを
考えた場合、普通に計算すると
\(65^2-35^2=65×65-35×35=4225-1225=3000\)
ってなって、これを暗算で計算するのは、難しいよね。
これを因数分解の公式\(x^2-a^2=(x+a)(x-a)\)を利用して解いてみると。。
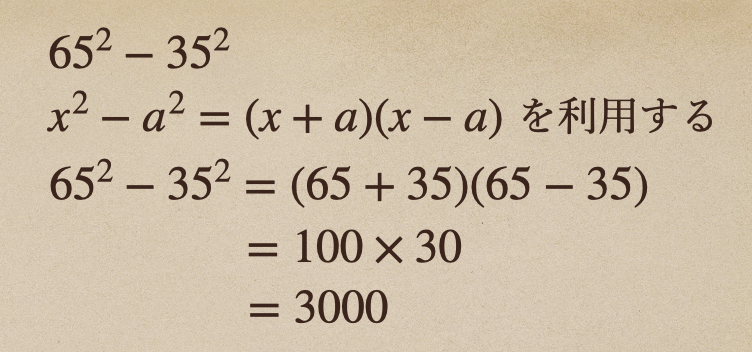
暗算でも計算しやすくなったよね。
この展開の公式や、因数分解の公式の利用っていうのは、
普段でもよく使う機会っていうのが多いので、ただ、計算するのではなく
いかに、計算を簡単に早くできるかっていうのを考えていくことを
意識していくようにしてみよう。
(3)式の値の計算
今度は、この問題を見てみて
問題:\(x=77\)、\(y=23\)のとき、\(x^2-y^2\)の値を求めよ。
この場合、みんなならどうやって計算するかな?
そのまま、\(x\)と\(y\)の値を代入して解く?
解:\(77^2-23^2=5929-529=5400\)…
2桁の累乗の計算をするのって、やっぱり抵抗があるよね
筆算して計算することはできるから、別に計算できないわけじゃないけど
大変だよね。
こんな時も、因数分解の公式を使って \(x^2-y^2=(x+y)(x-y)\)としてから
計算してあげると。。
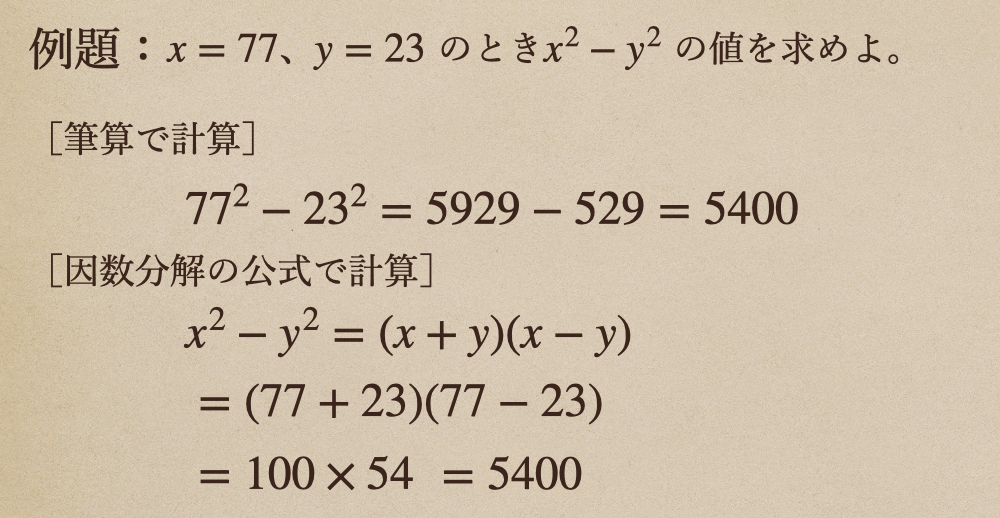
計算の式を書いていくと、因数分解の公式での解き方の方が多くなっているように
見えるんだけど。中身の計算って言うのは、簡単になっているよね。
こんな感じで展開の公式、因数分解の公式を使っていくこともできるってことなんだね。
(4)整数や図形の問題の利用
この多項式では、文字を使って数を表すってことをよく使われていて
それって言うのが。。

こんな風に表すことができるんだね。
\(m\) と \(n\) が整数であれば、それを2倍すれば必ず、偶数になるし
その偶数に\(1\)を足してあげれば、それは奇数になるってことだね。
これを利用した問題っていうのが。。

奇数を文字にして表して、それらの積の解っていうのが奇数であることを
証明したってことになるんだね。
今度は図形を使った問題を見てみよう。

問題としては、証明問題ってことになるんだけど、証明したい\(S=2ab\pi\)を
考えても、今の段階では、導き出すことはむずかしいよね。
この場合、まずは色をつけた部分の面積\(S\)っていうのを求めてあげよう。
ここで、ポイントになるのが色をつけている部分っていうのは大きな円になっていて
その直径はっていうと、円\(O\)の直径と円\(O’\)の直径の和ってことだよね。
ようするに、大きい円の半径はっていうと\(a+b\)として表すことができるよね。
これを元に、面積\(S\)を求めてみると。。

色のついた面積\(S\)を求めたら、\(S=2ab\pi\)になったので、これで\(S=2ab\pi\)が
証明されたってことだね。
ここでも、文字で式を作って、展開の公式から式を計算して求めていったってことになるね。
多項式の計算って言うのは、多くの場面で用いられることになるから
その計算の仕方であったり、展開の公式、因数分解の公式っていうのを使うことで
計算を時短することができるってことなんだね。
今回は、ここまでになります。
ここまでの記事が良かったと思ったらここをクリックしてね。
質問なんかがあった場合はコメントにお願いします。
では、またさようなら。



コメント