どうも、こんにちはDKです。
今回は中学3年生で習う「関数\(y=ax^2\)」の利用についてやっていきますね。
一つ前で関数\(y=ax^2\)についての基礎を説明しているので
そっちもよかったらみてみてください。
「関数\(y=ax^2\)」の利用では、文章問題から\(y=ax^2\)の形を作って
答えを求めていくんだね。ここでは、よく使われる問題を紹介しつつ、例題を交えて
解き方までを解説していきますね。
[1] 物体の落下
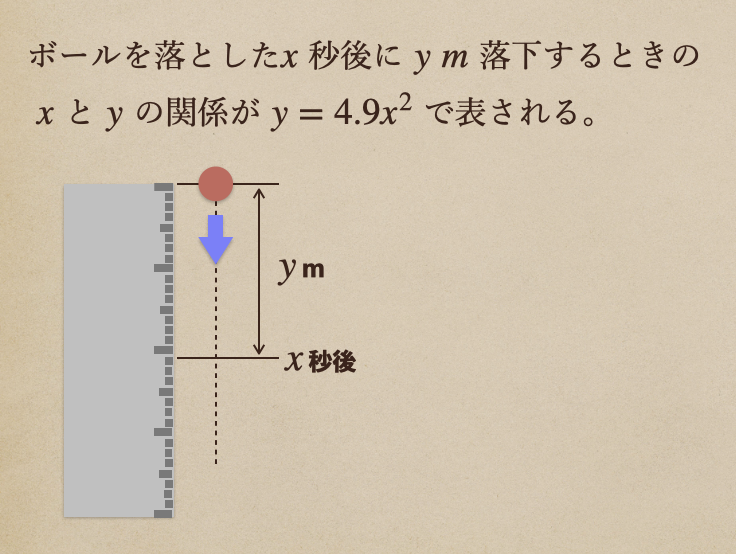
これは、ボールを落として\(x\)秒後に\(y\) \(m\)落下するときって言うのが
\(y=4.9x^2\)で表しますよ。ってことになるんですね。
この\(y=4.9x^2\)っていうのは、問題の中で提示してくれるのでわざわざ覚える必要は
ないので、物体を落下させるときって言うのは関数\(y=ax^2\)で表されるって言うのを
覚えておこう。
これを踏まえて例題を見ていきましょう。
例:地面から\(125m\)の高さからボールを落としたとき、落ち始めてから\(x\)秒後に
ボールが落ちた距離を\(y\) \(m\)とすると、\(y=5x^2\)の関係がある。
① 2秒後には、何\(m\)落ちるか求めなさい
②地面に落下するまでに何秒かかるか求めなさい
この問題では、関数が\(y=5x^2\)として表されているんだけど、問題によっては
比例定数をキリのいい数字に置き換えて表されることもあるんだね。
ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー
①2秒後ってことなので、これが\(x\)となるので、\(x=2\)ってことですよね。
なので、この\(x=2\)を\(y=5x^2\)に代入してあげて
\(y=5×2^2\)
\(y=20\)
ってことなので、2秒後には\(20m\)落下したことになりますね。
②地面までの距離は\(125m\)ってことなので、今度は\(y=125\)っていうのが
わかっているとなるので、これを\(y=5x^2\)に代入してあげて
\(125=5x^2\)
\(x^2=25\)
\(x=±5\)
となって、\(x≧0\)となるので、地面に落ちるまでの時間は\(5\)秒後ってことになりますね。
ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー
以上が物体の落下における関数\(y=ax^2\)になりますね。
[2] 振り子の長さ
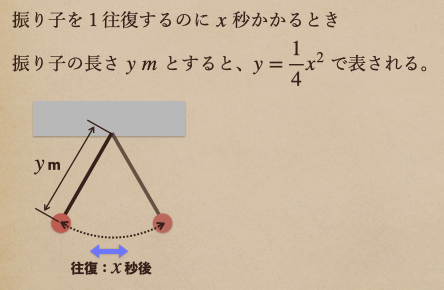
振り子の運動とその長さには関係があって、振り子を1往復するのに
\(x\)秒かかるときの振り子の長さ\(y\) \(m\)とすると\(y=\frac{1}{4}x^2\)で
表すことができるんだね。
これも、例題を見ていきますね。
例:長さ\(y\) \(m\)の振り子がある。この振り子が1往復するまでの時間を\(x\)秒と
したとき、その関係は\(y=\frac{1}{4}x^2\)で表される。
①1往復が2秒かかるとき、振り子の長さを求めよ
②振り子の長さが\(25cm\)のとき、1往復にかかる時間を求めよ
関数\(y=\frac{1}{4}x^2\)からそれぞれを求めてあげればいいってことになりますね。
ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー
①1往復が2秒ってことなので、\(x=2\)を\(y=\frac{1}{4}x^2\)に代入してあげて
\(y=\frac{1}{4}×2^2\)
\(y=\frac{1}{4}×4=1\)
\(y=1\)ってことなので、振り子の長さは \(1m\)ってことになりますね。
②振り子の長さが\(25cm\)ってことで、\(y=25\)を代入して\(x\)を求めるかって
言うと、これは間違いで、ここで注意しないといけないのは、振り子の長さが
\(25cm\)ってことで、この振り子の長さの関係は[長さ\(m\)と時間\(s\)]で
\(y=\frac{1}{4}x^2\)の関係が成り立っていることになるんですね。
なので、ここではまず、\(cm\)を\(m\)に直してあげる必要があるんですね。
\(y=25(cm)=0.25(m)=\frac{1}{4}(m)\)としてからこれを、\(y=\frac{1}{4}x^2\)に
代入してあげるってことですね。
\(\frac{1}{4}=\frac{1}{4}x^2\)
\(1=x^2\)
\(x=±1\)
となって、\(x≧0\)であることから、\(x=+1\)となって
振り子の長さ\(25cm\)の1往復する時間は\(1\)秒になるってことですね。
ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー
こう言った問題で注意するのは、単位があっているかしっかり確認して
解くようにしていきましょう。
[3] 車の制動距離
車は急には止まれないって言葉がありますよね。
それって言うのは車がブレーキをかけて車が停止するまでの間には
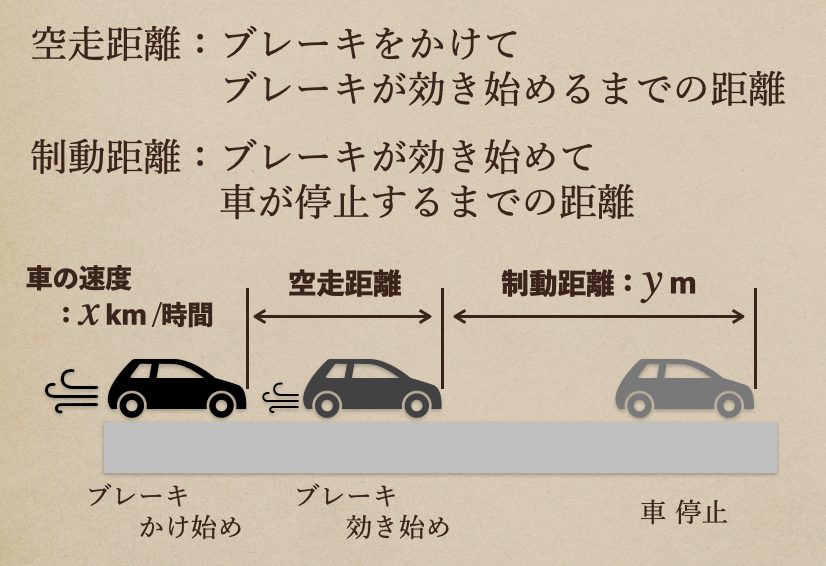
・空走距離:ブレーキをかけ始めてブレーキが効き始めるまでの距離
・制動距離:ブレーキが効き始めてから車が停止するまでの距離
の2つの距離があって、これらを足した和って言うのが「停止距離」って言うんですね。
そして、この「空走距離」は一般的に車の速さに比例するってことなんだけど
「制動距離」って言うのは、車の速さの2乗に比例しているってことなんだね。
なので、この「制動距離」って言うのは、車の速さを時速\(x\) \(km\)とすると
制動距離(車が停止するまでの距離)を\(y\) \(m\)とすると、\(y=ax^2\)で
表すことができますよってことなんだね。
例題見ていきますね。
例:時速\(x\) \(km\)で走っている車の制動距離が\(y\) \(m\)であったとき
\(y\)は\(x\)の2乗に比例する。このとき、時速\(60km\)で
走っている車の制動距離が\(24m\)であった。
①\(y\)を\(x\)の式で表しなさい
②この車が時速\(90km\)で走っているとき、制動距離を求めなさい
①で関数\(y=ax^2\)の比例定数\(a\)を求めて、②で\(x=90\)を代入してあげれば
いいってことになるね。
ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー
①\(y=ax^2\)に\(x=60\)と\(y=24\)を代入してあげて
\(24=a×60^2\)
\(24=3600a\)
\(a=\frac{24}{3600}\)
\(a=\frac{1}{150}\)
となるので、\(y\)を\(x\)で表すと、\(y=\frac{1}{150}x^2\)となるってことだね。
②\(y=\frac{1}{150}x^2\)に\(x=90\)を代入してあげて
\(y=\frac{1}{150}×90^2\)
\(y=\frac{8100}{150}\)
\(y=54\)
となるので、時速\(90km\)で走る車の制動距離は\(54m\)ってことになりますね。
ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー
ここでも、\(x\) \(km\)と\(y\) \(m\)で単位が違っているので注意しておこう。
[4] 図形の中に現れる関数
この項では、実際に例題を使ってどういったものかって言うのを説明していきますね。
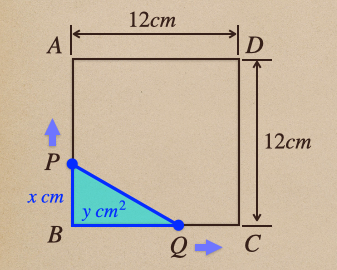
例:1辺が\(12cm\)の正方形\(ABCD\)がある。点\(P\)、\(Q\)は点\(B\)を
同時に出発して、点\(P\)は辺\(AB\)を毎秒\(1cm\)で点\(A\)まで進み
点\(Q\)は辺\(BC\)を毎秒\(2cm\)で点\(C\)まで動く。
点\(P\)、\(Q\)が\(B\)を出発してから\(x\)秒後の\(\triangle{PBQ}\)の
面積を\(y\)\(cm^2\)としたとき
①\(5\)秒後の\(\triangle{PBQ}\)の面積を求めなさい
②\(\triangle{PBQ}\)の面積が\(9cm^2\)となるのは
何秒後か求めなさい。
こういった図形を使った問題が出題されるケースがよくあって
この問題でどこに関数\(y=ax^2\)が出てくるかって言うのは問題を
解いていけばわかってくるので、問題を解きながら確認していってみよう。
ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー
①まずは、\(triangle{PBQ}\)の面積を求めようと思うと
辺\(PB\)と辺\(BQ\)の長さがわかれば三角形の面積が求めることができる
それぞれ、\(x\)秒後の辺\(PB\)と辺\(BQ\)の長さは
\(PB=x\)、\(BQ=2x\)として表すことができる。ここから
\(\triangle{PBQ}=y=\frac{1}{2}×x×2x\)
\(y=x^2\)
ここに、\(x=5\)を代入して
\(y=5^2=25\)
なので、\(5\)秒後の\(\triangle{PBQ}\)の面積は\(25cm^2\)となる。
ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー
三角形の面積を求めてあげたら、\(y=x^2\)となるのでここで
関数\(y=ax^2\)が出てきたってことだね。
続けて②を解いていくよ。
ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー
②今度は、\(\triangle{PBQ}\)の面積がわかっているってことなので
\(y=9\)を代入してあげて
\(9=x^2\)
\(x=±3\)
\(x\)は\(P\)、\(Q\)が進む時間なので、\(x≧0\)なので
\(x=3\)となって、
\(\triangle{PBQ}\)の面積が\(9cm^2\)となるのは\(3\)秒後となる。
ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー
関数\(y=ax^2\)を求めることができれば、答えを求めていくだけになるね。
始めの関数の式を導き出すところが文章問題では一番大事なところと
なってくるってことだね。
[5] いろいろな関数
今度は、関数\(y=ax^2\)ではないんだけど、他にも関数となるものがあるんだね。
(1) グラフが階段状の関数
グラフが階段状になっている関数ってことなんだけど、??どういうこと??
ってなるんだけど、例えば下の表はD鉄道の運賃を表したもので
初めは180円からスタートして乗り込んだ駅から2駅ごとに20円ずつ運賃が
増していき8駅以上は運賃が一律260円になっているものを表しているんですね。

これを、グラフで書くとこんな感じになっている関数で
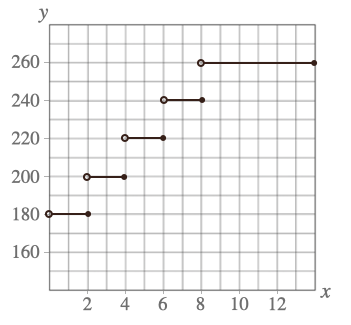
今までにない、グラフになりましたよね。
こう言った形のグラフの関数もあるってことなんだね。
これは、\(x\)と\(y\)の関係は次のようになっているってことなんだね。
\(0≦x<2\)のとき\(y=180\)
\(2≦x<4\)のとき\(y=200\)
\(4≦x<6\)のとき\(y=220\)
\(6≦x<8\)のとき\(y=240\)
\(8≦x\)のとき\(y=260\)
このグラフで、「⚪︎」で表してあるところはその値をふくんで
「⚫︎」で表してあるところはその値はふくまないってことになるんだね。
この見方をグラフを書くときやグラフから読み取るときに
間違えてしまうしまうので注意が必要だね。
(2) 2倍ずつ増える関数
これも、例を見ながら考えてみよう。
ここに紙があって、これを半分に切って、切り取った紙を重ねて
さらに半分に切って、また切り取った紙と元の紙をすべて重ねて
これまた半分にするといった具合に、これを繰り返し行なって
\(x\)を切り取った回数として、\(y\)を\(x\)回切ったときの
紙の枚数として、これを表にしてあげると。。

これを\(y\)を\(x\)の式で表してあげると
\(y=2^x\)
となるんだね。こう言った関数もあるってことなので覚えておいて。
今回は、ここまでになります。
ここまでの記事が良かったと思ったらここをクリックしてね。
質問なんかがあった場合はコメントにお願いします。
では、また、さようなら。
.jpeg)


コメント