どうも、こんにちはDKです。
今回は中学3年生で習う三平方の定理についてやって行きますね。
三平方の定理って聞いてもなんのことか想像することはむずかしんだけど
これは別の言い方でピタゴラスの定理とも言うんだね。
なんでも、紀元前500年ごろにギリシャのピタゴラスとう言う数学者が
石畳の形から直角三角形の辺の上にできる図形の面積に関係性があることに
気づいたことで発見された定理と言われているんだね。
歴史に興味のある人はピタゴラスで調べてみて。
ここでは、そのピタゴラスが発見した三平方の定理がどういったものなのかって言うのを
解説していきますね。
ちなみに、この三平方の定理は万能で、これがわかることでいろんなところの
辺の長さって言うのを求めていくことができて、とても重要な単元となっているので
しっかり、理解して行ってくださいね。
それでは、こっちの「三平方の定理」についてやって行きますね。
1.三平方の定理
直角三角形を見たときに、各辺を1辺とする正方形の面積っていうのは
次のことが言えるんだね。
「直角をはさむ2辺をそれぞれ1辺とする2つの正方形の面積の和は
斜辺を1辺とする正方形の面積に等しい」
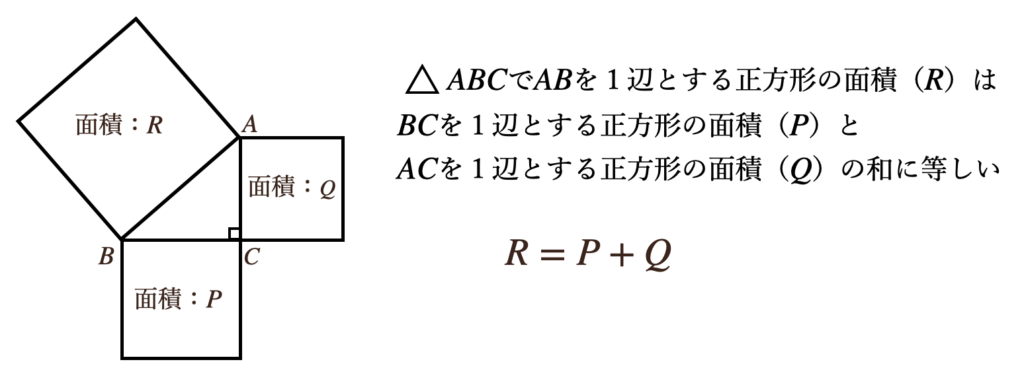
このことから、\(AB\)、\(BC\)、\(AC\)の辺をそれぞれ、\(a\)、\(b\)、\(c\)としたとき
それぞれの正方形の面積は、\(R=c^2\)、\(P=a^2\)、\(Q=b^2\)となるので
\(R=P+Q\)は\(c^2=a^2+b^2\)と置き換えてあげることができるんだね。
ようするに、直角三角形の3つの辺の長さについて次の定理があるんだね。

実際にこの三平方の定理が成り立つのかを証明して確認してみよう。
証明の仮定は「\(\triangle{ABC}\)は\(\angle{C}=90^\circ\)の直角三角形」で
結論は「\(c^2=a^2+b^2\)」として証明していきますね。

こんな風に、直角三角形の斜辺を1辺とした正方形を作ってあげて
2つの正方形の面積で等式を作ってあげて、それぞれに辺の長さを当てはめて
\(c^2=a^2+b^2\)であることを証明することができているんだね。
これで、「三平方の定理」っていうのは正しいってことになるんだね。
次にこの三平方の定理で直角三角形の辺の長さを求めることが
できるようになったので、実際の辺の長さを求めて行ってみよう。
2.直角三角形の辺の長さ
さっそく、次の問題を解いてみよう。
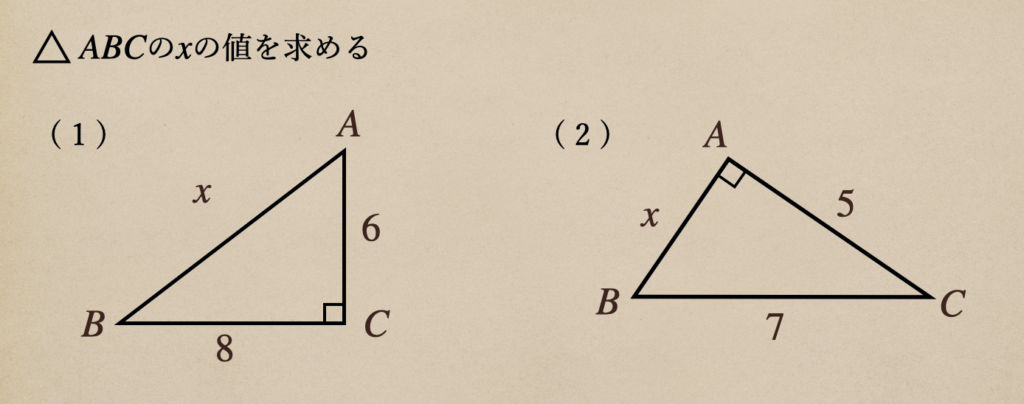
三平方の定理を使って次の図形の\(x\)の値を求めてみよう。
注意する点としては、直角三角形の斜辺以外の辺の長さの2乗の和が斜辺の長さの2乗と
等しくなるってことだね。
(1)から\(x\)を求めていくよ。
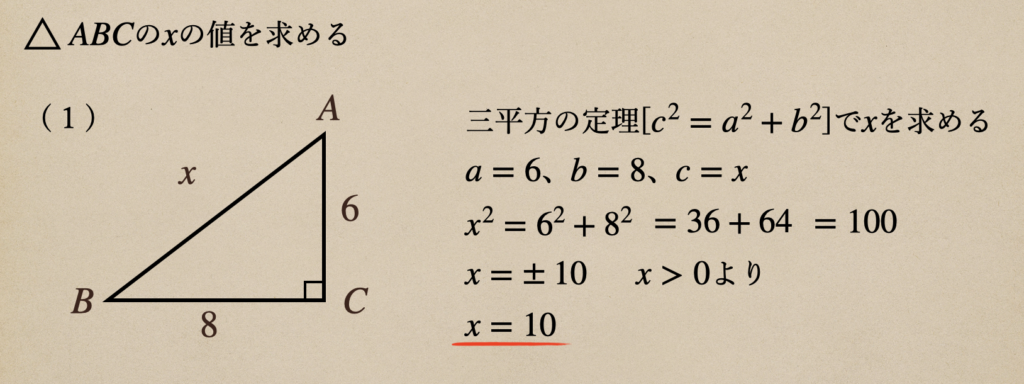
\(x\)の2乗を取ってあげて、平方根を求めてあげるんだね。
\(x\)は図形の辺になるので、負の数ってことはないので\(x>0\)ってことで
\(x=10\)となるってことなんだね。
じゃあ、次は(2)の\(x\)を求めていくね。
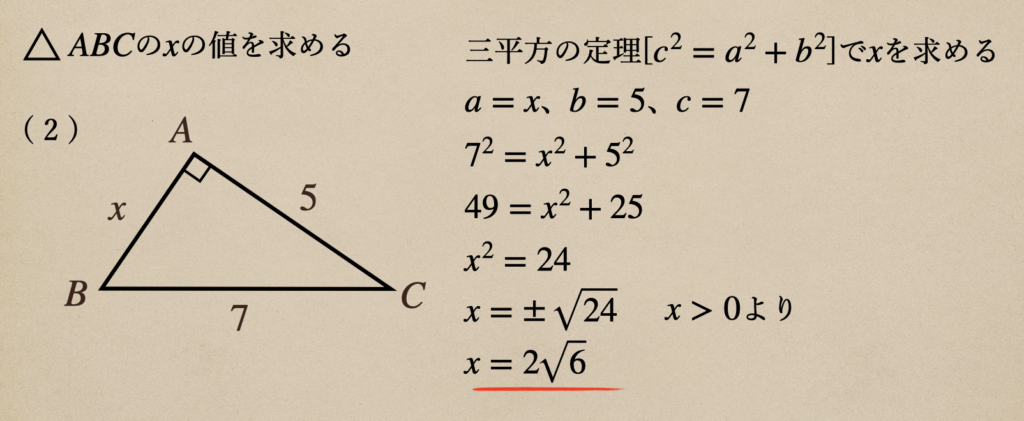
(2)の場合は、斜辺が\(7\)で\(x\)は\(a\)(もしくは\(b\))となるんだね。
\(x\)の2乗をなくしてあげて、平方根を求めてあげると整数ではなく、ルートとなっても
それが答えってことになるんだね。
ちなみに、この三平方の定理[\(c^2=a^2+b^2\)]で\(a\)、\(b\)、\(c\)が
整数となる組み合わせっていうのは、決まっていて次のような組み合わせになるんだね。

よく使われるのは赤わくで囲った\(a=3\)、\(a=4\)、\(a=5\)の組み合わせになるので
覚えておこう。他の組み合わせも可能な限り、覚えておけるとテストで役に立つよ。
3.三平方の定理の逆
ここまでで、三平方の定理から直角三角形であれば、\(c^2=a^2+b^2\)であることが
言えるってことがわかったので、今度は三角形の3辺が\(c^2=a^2+b^2\)であれば
その三角形は直角三角形であることが言えるかを考えてみよう。
ここに①、②の2つの三角形があって
①の三角形は\(AB=5cm\)、\(BC=4cm\)、\(CA=3cm\)で
②の三角形は\(EF=4cm\)、\(FD=3cm\)、\(\angle{F}=90^\circ\)だったとき
①の三角形が直角三角形であることを証明することで\(c^2=a^2+b^2\)であれば
直角三角形であることを証明できるんってことになるんだね。
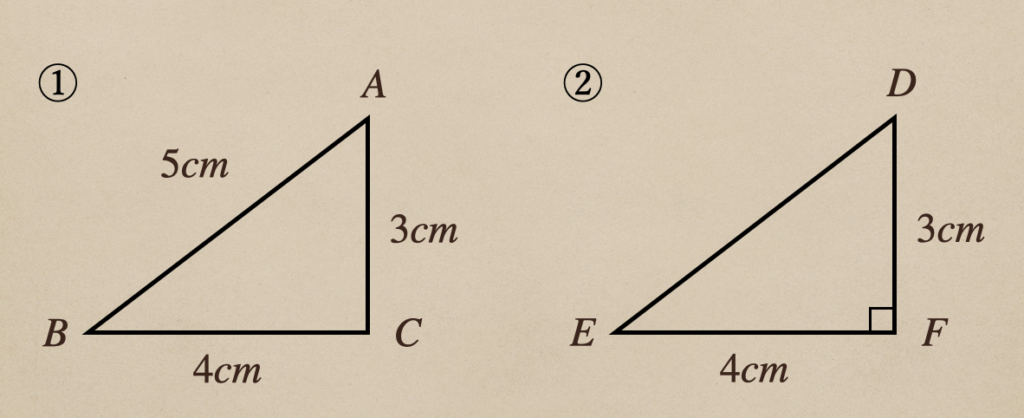
①の三角形が直角三角形かを証明するのであれば、①と②が合同であることを
証明できれば、対応する角が等しいことが言えるので、\(\angle{C}=90^\circ\)で
あることが言えるので、①の三角形が直角三角形であることが証明できることになるね。

これで、証明することができたので、三平方の定理の逆として
次のことが言えるんでね。

「長さ\(c\)の辺を斜辺とする」っていうのも気をつける点になるね。
ここまでが三平方の定理の前半の解説が終わりで、次の項では
三平方の定理を使って図形や座標平面から長さを求めるっていうのを
立っていきます。
今回は、ここまでになります。
ここまでの記事が良かったと思ったらここをクリックしてね。
質問なんかがあった場合はコメントにお願いします。
では、また、さようなら。



コメント