どうも、こんにちはDKです。
じゃあ、さっそく中学数学の基礎をやっていきますね。
その前に、このブログでの内容は動画でも解説してるよ。
※動画再生は音が出るから注意してね。
正(せい)の数・負(ふ)の数
今回は”正(せい)の数・負(ふ)の数”について学んでいくね。
小学校までの算数でいろいろな計算してきたよね?足し算、引き算、かけ算、わり算・・・
けど、使ってきた数字は0、1、2、3、4とかだよね?

これって、実は0を含む正の数を言ってるんだ。
ようするに、”正の数”とは『0より大きい数』のことを言うんだね。
ここで注意しとくことは0は”正の数”には含まなれないよ。
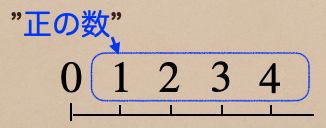
じゃあ、負の数は?ってなるよね。
”負の数”と言うのは『0より小さい数』のことを言うんだね
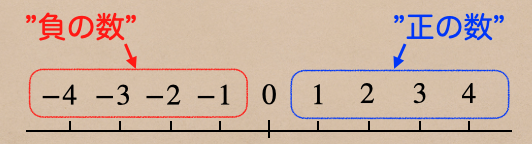
ここで、負の数の前に”ー”がついていることに気づいた?
これは「マイナス」と言う呼び方をして、”−1”の場合「マイナスいち」と呼ぶんだよ。
この「ー(マイナス)」のことを負の符号と言うことも覚えておいてね。
正の数は”1”、”2”と、何もつけないで今まで通り呼ぶこともできるし、
”+1”、”+2”と書くこともできるよ。呼び方は「プラスいち」、「プラスに」と言うんだよ。
「+(プラス)」のことは正の符号と言うのも覚えておこうね。
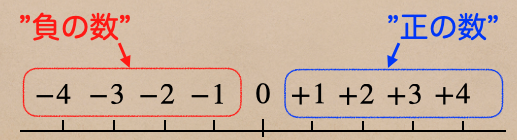
ここで簡単におさらいしておくね。
正の数・・・0より大きい数
「+(正の符号)」で表す
負の数・・・0より小さい数
「ー(負の符号)」で表す
※正の数も負の数も0を含まない数字
すべてになるから小数や分数も含まれるよ。
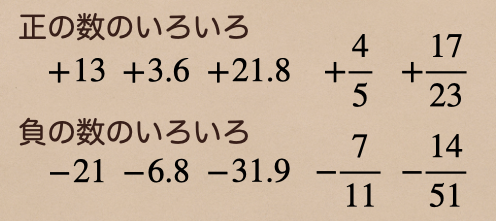
ここまでは、理解できたかな?
次は〇〇数について学んでいくね。
整数、自然数
整数、自然数はよく問題でも出てくるのでしっかり学んでおこうね。
整数とは0、正の数、負の数で小数、分数を含まない数を指しているよ。
自然数とは正の整数のことを言ってるんだ。
ちなみに小数とは小数点が含まれる数のことで、分数とは分母と分子で表している数を言うよ。

この整数、自然数、小数なんかはむずかしいわけではないんだけど、すごく混乱しやすいから
すぐに、あれっ自然数でなんだっけ?みたいになっちゃうので、しっかり理解しておこうね。
[〇〇数まとめ]
- 実数:全ての数字のこと(整数、自然数、小数、分数)
- 正の数:実数の中で0より大きい数
- 負の数:実数の中で0より小さい数
- 整数:0を含む正の数、負の数で小数、分数を含まない数
- 自然数:正の整数
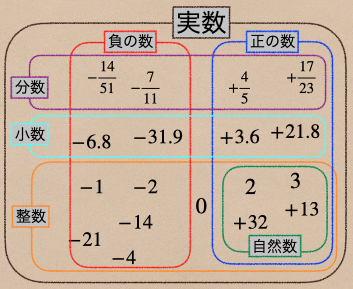
どうだったかなって思い出したいときに図で覚えておくと思い出しやすかったりするから
イメージで覚えるのもいいね。
じゃあ、次は数直線を学んでいこうね。
数直線
数直線って言うのは直線上に数を対応させて表した図のことで
正の数、負の数の説明の時に僕が図で表していたものを言うんだよ。
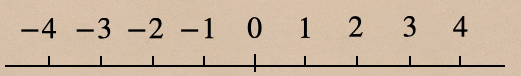
↑こんなやつのことだね。
数直線は一般的に右にいくほど大きい数を表して、左にいくほど小さい数を表すんだね。
数直線で注意することは上の説明にも書いた通り”数を対応させて表す”から
必ず、-3、-2、-1、0、1、2、3のように連続した数字になるとはかぎらないよ。
例えば…
①-4、-3、-2、-1、0、1、2、3、4で引いた数直線
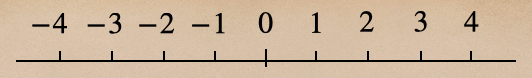
②-8、-6、-4、-2、0、2、4、6、8で引いた数直線
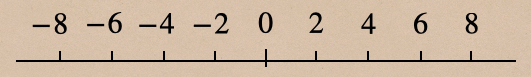
③-40、-30、-20、-10、0、10、20、30、40で引いた数直線
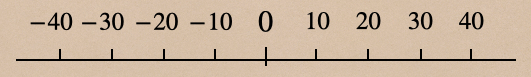
それぞれ、一つの目盛りがちがうよね、こんな感じでどの数に
対応した数直線かをしっかりと理解する必要があるよ。
ポイントとして、数直線の並び方には規則性があることを理解しておけば
どの数に対応した数直線か見つけやすくなるよ。
上の例の場合
①は1ずつ増える、減る数字で並んでいるよね。
②は2ずつ増える、減る数字で並んでいるよね、ようするに偶数の並びになっているんだよ。
③は10ずつ増える、減る数字で並んでいるね。
理解できたかな?
正の数、負の数についてわかったかな?今度はこの正の数、負の数をどうやって使っていくかを
理解しようね。
正の数、負の数で量を表す
反対の性質をもつ量や基準を決めたときの量を正の数、負の数で表すことができるんだ。
例えば、山の高さ3500m、海の深さ5500mの場合、下の図のように表すことができるんだね。
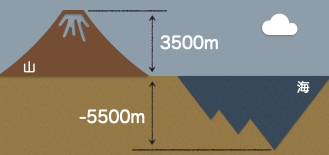
他にも、お金の収入や支出なんかでも正の数、負の数が使われるよ。
ハナコさんは3000円のお小遣いをもらって、500円の本を買いました。
収入:3000円 支出:−500円 みたいにね。
こんな感じで、基準を決めて、その基準からの増えた、減ったで正の数、負の数を表すことができるんだね。
他にも、目標を基準にして正の数、負の数を表すこともできるんだ。
一郎くんはバスケットの試合で15得点を取ることを目標にしていたとするね。
この時、目標としていた得点に対して
20得点すると ・・・+5得点
12得点とすると・・・ー3得点
と表すことができるんだね。
色々な時に正の数、負の数は使うから、しっかり使い慣れていこうね。
次は絶対値と数の大小について学んでいくね。
絶対値
絶対値とは数値線上で0からのある数の距離までを言うんだ。
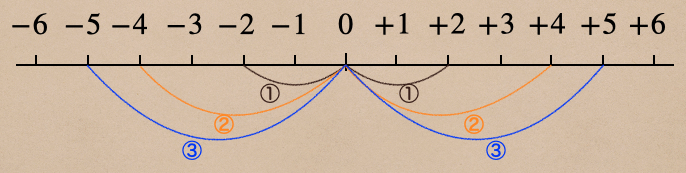
①の場合、0から+2および−2までの距離は”2”だよね。
②の場合、0から+4および−4までの距離は”4”だよね。
③の場合、0から+5および−5までの距離は”5”だよね。
この”2”、”4”、”5”を絶対値と言うんだ。
+2の絶対値は2。−4の絶対値は4。と言った言い方をするんだよ。
絶対値って言うのは距離を表しているため、+やーの符号を付けずに言う必要が
あるんで、間違えないようにしようね。
また、+2に対して−2や+4に対して−4みたいに、+、ーの符号を入れ替えて数を呼ぶ時は
「符号を変える」って言うんだよ。
次は正の数と負の数の大小について学んでいくね。
数の大小
正の数と負の数の大小は数値線上に表すとわかりやすくて、数値線の右にいくほど大きくなって
左に行くほど小さくなるんだよ。
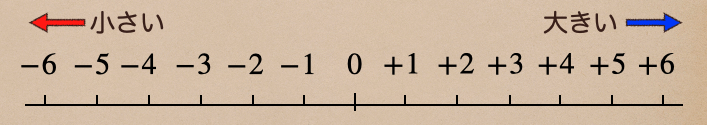
不等号(<、>)を使って数の大小を表すとこんな感じになるよ。
2<5 −5<2
−4>−5 −5<−4
ここまでが、正の数と負の数の基礎となる部分になるよ。これからの数学では
ここが基本となっていくから、しっかりと理解して次に進めようね。
じゃあ、次は正の数、負の数を使った計算を学んでいくね。
ここまでの記事が良かったと思ったらここをクリックしてね。
コメントもくれるとうれしいな。





コメント