どうも、こんにちはDKです。
今回は中学2年生で習う、1次関数の続きやっていきますね。
ここの解説に入る前に、1次関数、1次関数のグラフの書き方なんかが
わかっていないって人は1次関数のグラフをもう一度、見直しを行なって
1次関数がどう言ったものだったかっていうのをしっかり確認してから進めていって下さいね。
ここでの解説は動画でも行なっているよ。(※音が出るから注意)
(1)2元1次方程式のグラフ
1次関数に関しては、理解してもらえたかと思うので
ここからは、連立方程式でもやってきた、2元1次方程式のグラフって言うのを
見ていってみよう。
2元1次方程式\(2x+y=5\)の解は?ってなると。。
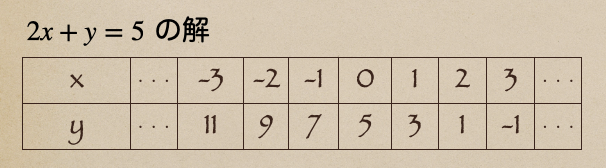
値の組を書き出すとこうなるよね。そして、これをグラフに書いていくと。。
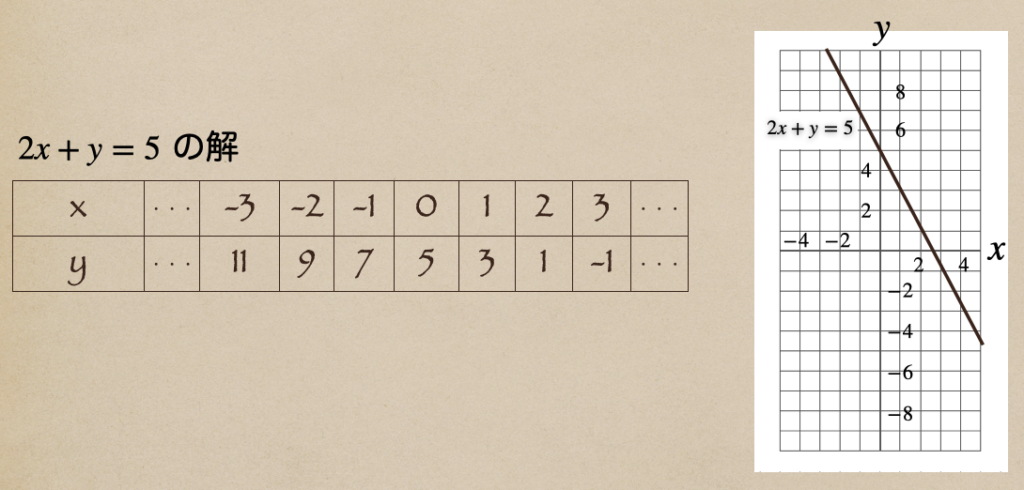
こんなグラフになるんだね。
2元1次方程式\(ax+by=c\)の解( \(x\) 、\(y\) )を座標とする点の集まりを
2元1次方程式のグラフと言う
また、2元1次方程式\(ax+by=c\)のグラフは直線となる( \(a,b,c\)は定数 )
ところで、2元1次方程式\(2x+y=5\)って\(y\)について解けば
\(y=-2x+5\)ってなるよね。これって言うのは1次関数ってやつだったよね。
ってことは。。
2元1次方程式のグラフは、その方程式を\(y\)について
解いたときの1次関数のグラフと一致する

ようするに、2つの方程式はどちらも、同じものってことになるんだね。
(2)2元1次方程式のグラフの書き方
実際に2元1次方程式が会った時にそれをグラフに書く場合
さっきみたいに、値の組を表に書き出していって、座標に書いてグラフを書くなんて
やっていけないよね。なので、2元1次方程式のグラフの書き方って言うのは
2元1次方程式\(ax+by=c\)を\(y\)について解いて
\(y=-\frac{a}{b}x+\frac{c}{b}\) となって
傾き \(-\frac{a}{b}\)、切片 \(\frac{c}{b}\)のグラフをひく
結局のところ、1次関数に直して、傾きと切片からグラフをひいてあげる
やり方になるんだね。
(3)2元1次方程式\(ax+by=c\)で、\(a=0\)や\(b=0\)の時のグラフ
2元1次方程式\(ax+by=c\)で、\(a=0\)や\(b=0\)の時のグラフって言うのが
どう言ったものになっていくのかを見ておこう。
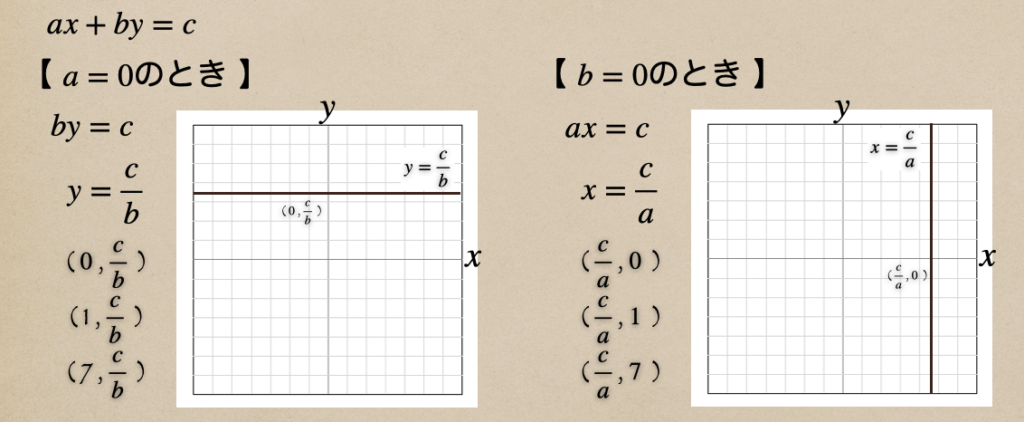
\(a=0\)のときは\(y\)だけの式になるってことで、\(x\)の値がどれになっても
\(y\)は\(\frac{c}{b}\)になるってことなんだね。
同様に\(b=0\)のときは\(x\)だけの式になるってことで、\(y\)の値がどれになっても
\(x\)は\(\frac{a}{b}\)になるってことなんだね。
また、それぞれのグラフって言うのは
\(x=\)〜のグラフ・・・\(y\)軸に平行となる
\(y=\)〜のグラフ・・・\(x\)軸に平行となる
特徴的なグラフになるね。よく、逆に直線をひいてしまうので注意しよう。
(4)グラフと連立方程式
次はグラフと連立方程式ってところになるんだけど
2元1次方程式のグラフと1次関数って言うのは、同じようにグラフに
することができることはわかったよね。
ってことは、連立方程式も2元1次方程式が2つあるってことなので
グラフにすることができるよね。
けど、連立方程式って言うと、\(x\)の値と、\(y\)の値の組が一つだったよね。
これってグラフで書いたらどうなるんだろう。
実際にどうなるか、確認してみよう。
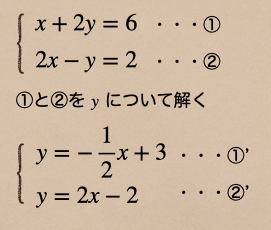
連立方程式があって、2元1次方程式のグラフの書き方で説明したように
①、②の式を\(y\)について解いて、①’、②’になるよね。
あとは、①’ だと、傾きが\(-\frac{1}{2}\)で切片が\(3\)でグラフを書いて
②’ だと、傾きが\(2\)、切片が\(-2\)でグラフを書けばいいので。。
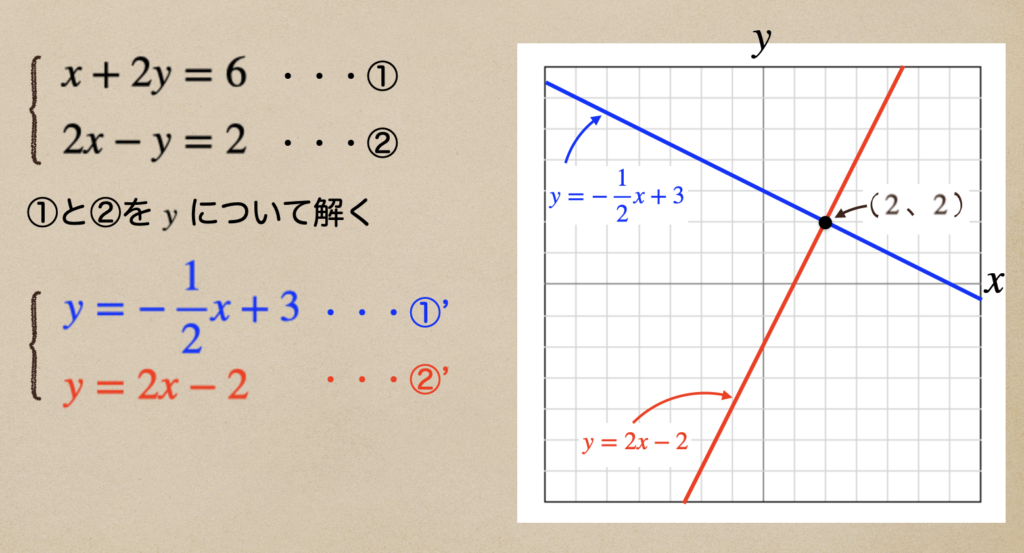
わかりやすいように色をつけて、グラフをひいて見たんだけど
ここで、注目しするのは、①’のグラフと②’のグラフの交点っていうのが
\((x,y)=(2,2)\)になっているんだけど、これっていうのが
この連立方程式の解にもなっているんだね。実際に連立方程式の解があっているか
確認してみよう。
ちなみに、連立方程式の解がわかっているから、確認の仕方は、解くだけではなく
解をそれぞれの式に代入して、成り立つかを確認する方法でもできるよ。

どちらの方法でも、解があっていることが確認できたね。
今までのは、2元1次方程式からグラフを書いていたよね
今度は、2本のグラフからその交点の座標を求めるっていうのをやっていくね。
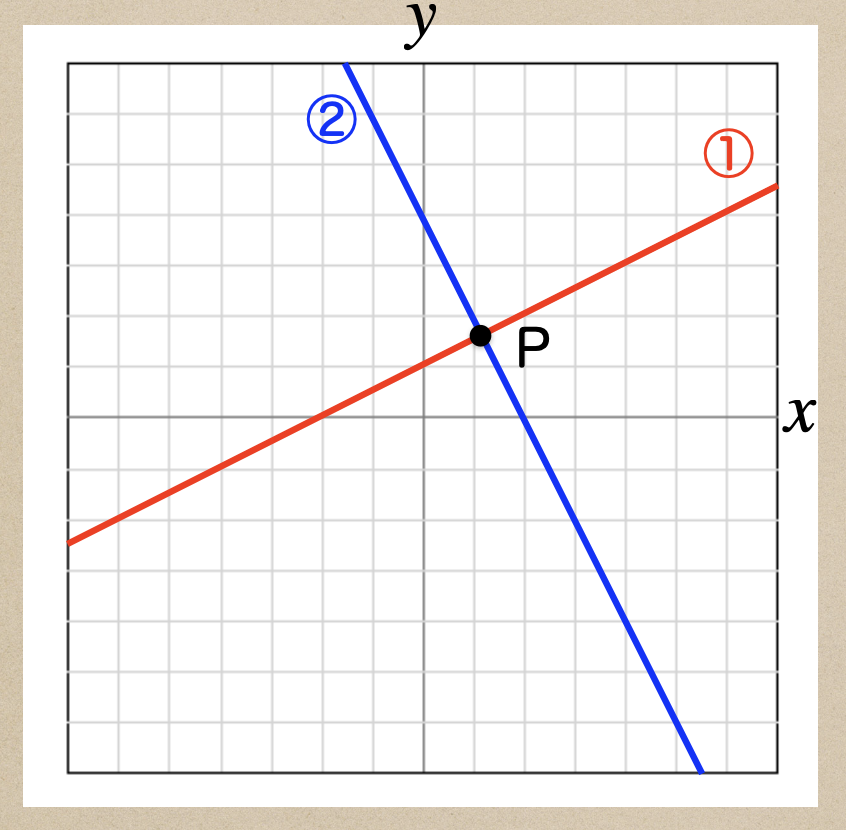
こんな風にグラフだけ書いてあるところから交点である点Pの座標を
求めるってことだね。
点Pが罫線上にないので、正確な座標ってのがこのままではわからないよね
こんな時は、それぞれのグラフの1次関数の式を求めてあげて、連立方程式の解を解いて
あげるっていうやり方になるんだね。
じゃあ、グラフから1次関数の式はどうやったらわかるかな?
それは、傾きと切片を求めてあげれば1次関数の式を作ることができる
だったよね。
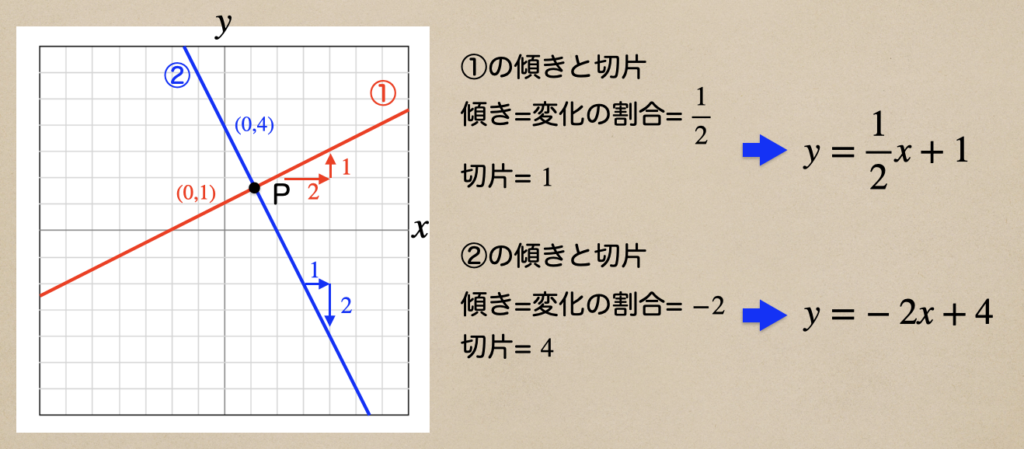
傾きは変化の割合で、(\(y\)の増加量)/(\(x\)の増加量)で求められて
切片はっていうと、\(x=0\)の時の\(y\)の値ってことなので、\(y\)軸とグラフの交点が
切片になるんだね。
傾きと切片が分かれば、\(y=ax+b\)に傾き(\(a\))と切片(\(b\))に値を
代入してあげればいいってことだね。
あとはこの2つの1次関数の式で連立方程式を解いてあげれば
交点Pが求められるってことだね。連立方程式の途中式は、ここでは飛ばして
交点Pの座標は(\(\frac{6}{5},\frac{8}{5}\))になるね。
ここの2つのグラフから交点を求めるっていうのは、よくテストにも出てくるので
しっかり、理解しておいてください。
今回は、ここまでになります。
ここまでの記事が良かったと思ったらここをクリックしてね。
質問なんかがあった場合はコメントにお願いします。
では、またさようなら




コメント