どうも、こんにちはDKです。
今回は中学2年生で習う、1次関数の続きやっていきますね。
ここの解説に入る前に、1次関数、1次関数のグラフの書き方なんかが
わかっていないって人は1次関数のグラフ、方程式とグラフをもう一度、見直しを行なって
1次関数がどう言ったものだったかっていうのをしっかり確認してから進めていって下さいね。
動画でも、解説しているよ。(※音が出るので注意して。)
1次関数の利用
今回は1次関数の利用ってところで、これはいろいろな状態を
1次関数の式やグラフに表していくってことなんだね。
いろいろな状態っていうは。。
(1)量と1次関数
バネの長さ、水量、水温などの変化の様子を表すグラフ
(2)図形と1次関数
面積の変化をグラフに表す
(3)速さと1次関数
時間と道のりの関係をグラフに表す
この3つと1次関数のグラフとしていくのかっていうのを
それぞれ、解説していくね。
(1)量と1次関数
バネの長さ、水量、水温なんかの変化を1次関数で考えて
グラフにしたり式にしていくってことなんだね。
一つずつ見ていってみよう。
①バネの長さ
バネっていうのは、引っ張れば伸びるよね。
その伸びた長さっていうのを\(y\)として、どんな変化で伸びていったのかを
グラフにしたりするってことなんだね。
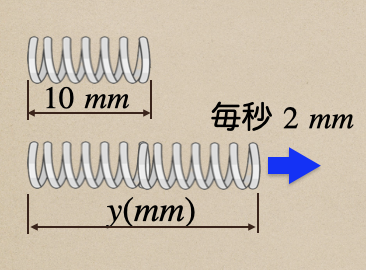
上の図の場合だと、引張っていない状態で\(10mm\)のバネを毎秒\(2mm\)で
引張っていった時のバネの長さを\(y\) \(mm\)としたとき
\(x\)秒の時の長さ\(y\) \(mm\)で1次関数を作れば、良いってことだね。
なので、式は \(y=2x+10\) ってなるね。
1秒で\(2mm\)伸びてるってことなので\(x\)秒後は\(2x\) \(mm\)伸びてるってことだよね。
そして、バネは元々、\(10mm\)の長さがあったので、全長はっていうと\(y=2x+10\) に
なるってことだね。これをグラフに書くと。。
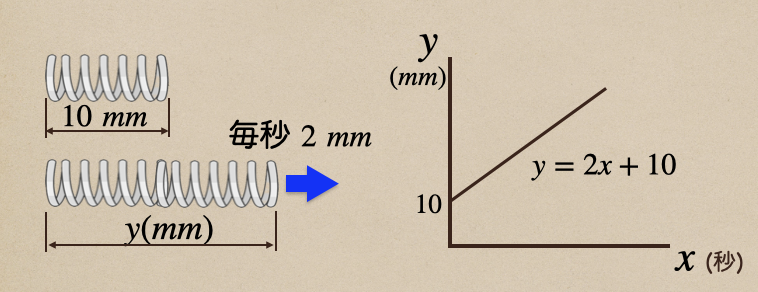
こんなグラフだね。\(y\)軸上を\(10mm\)から始まって
傾き2で右上がりのグラフになるってことだね。
②水温
今度は、水温の変化を1次関数で考えてみよう。

水温が15℃の水の入った容器を温めたとき、20分後に水の温度が55℃になった時
水温の変化が右側のグラフのように書くことができるね。
この時の1次関数の式を作ってみよう。\(x\)分後の水温\(y\)℃として見て
ここで、わかっている値は水温\(y\)℃、時間\(x\)分、初めの水温15℃ってことなので、
式は\(y=ax+15\)ってことだね、ここでわかったいないのでが、このグラフの傾き
ようするに、\(x\)分後に何℃温度が上昇したのかって言う傾きだね。
傾きを求めたい場合は、変化の割合[\(y\)の増加量]/[\(x\)の増加量]が分かれば
良いってことだったよね。なので、
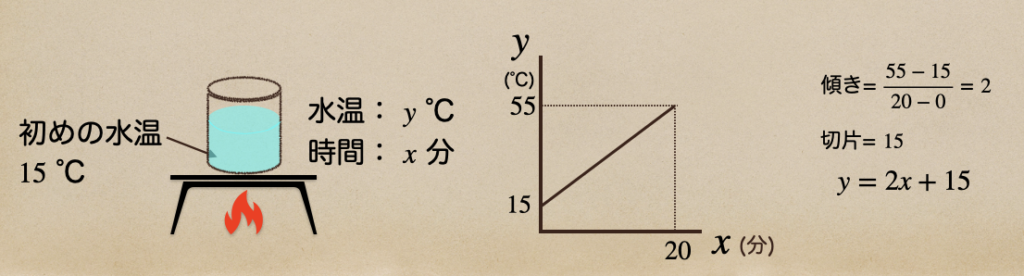
[\(y\)の増加量]/[\(x\)の増加量]=\(\frac{55-25}{20-0}=2\)となって、
1次関数の式は、\(y=2x+15\) になるってことだね。
③水量
次は水量の変化を1次関数で見てみよう。
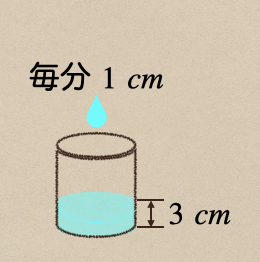
今度は、水面の高さが\(3cm\)まで、水が入ったようにき。
毎分で\(1cm\)水面の高さが増えるように水を入れたとき
この時の1次関数の式とグラフを書くってことだね。
これは、水面の高さを\(y\)として、\(x\)分後の水面の高さを式に書いていくってことだね。
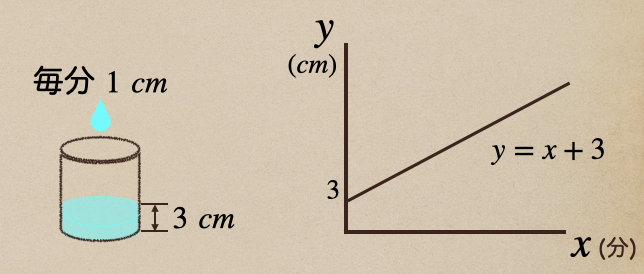
傾きが 1 、切片は3 で式が書かれているってことだね。
こんな風に量の変化の様子を1次関数に表したり、グラフにしていくってことだね。
量の変化っていうのは、今回、解説した内容以外でもいろいろあるので
確認してみてください。
(2)図形と1次関数
2つ目に図形と1次関数についてやっていきますね。
ここでは、本当にいろいろな使われ方をするので、代表的なもので
解説しておきますね。
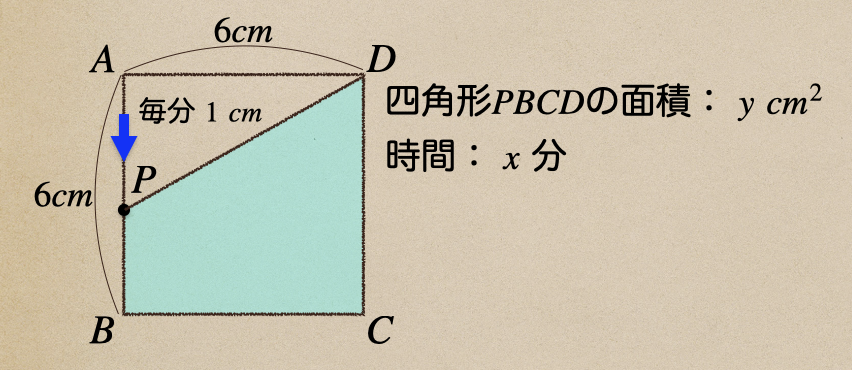
四角形\(ABCD\)があって、点Aから、点Bまで点Pが毎分\(1cm\)で進んだ点をPとして
この時の四角形\(PBCD\)の面積の変化っていうのを1次関数で見ていって見ましょう。
点Pっていうのは1分で\(1cm\)進むってことなので
\(x\)分後は\(x\)\(cm\)進むってことになるね。
そして、△\(APD\)の面積はっていうと、\(x\)\(cm\)を底辺として
高さ\(6cm\)となるので、\(y=\frac{1}{2}×6×x=3x\) となるので
四角形\(PBCD\)の面積は四角形\(ABCD\)の面積から△\(APD\)の面積を
ひいてあげれば良いってことだね。

1次関数の式は \(y=-3x+36\) となって、グラフは上図のようになるんだね。
ここで、このグラフが途中で途切れていることになるんだけど、これっていうのが
点Pは点Aから点Bまでを移動するってことだったので、点Bに着いたときの
時間は6分後で四角形\(PBCD\)は三角形\(PCD(BCD)\)になっているってことだね。
なので、この時の面積\(y\)はっていうと、四角形\(ABCD\)の面積の半分になるので
\(y=18cm^2\)になるってことだね。ようするにこの1次関数には変域があるってことになるんだね。
今度は、点Pが点Bから点Cまで移動した時っていうのを考えてみよう。
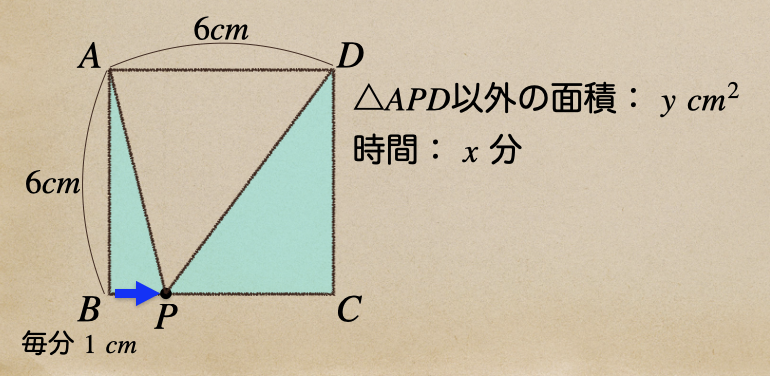
今度も△\(APD\)の面積以外のところなので
△\(ABP\)の面積と△\(PCD\)の面積を\(y\)\(cm^2\)とするってことだね。
面積2つを求めないといけないってことなので
めんどくさいって思うかもしれないけど
さっきと同じように、四角形\(ABCD\)の面積から△\(APD\)の面積をひいてあげれば
△\(ABP\)の面積と△\(PCD\)の面積である\(y\)\(cm^2\)を求めることができるよね。
ただ、今回のポイントは三角形の面積の性質で、底辺が同じで高さが同じであれば
どんな形の三角形も面積は同じになるでしたよね。
点Bから点Cまでの移動で、△\(APD\)の面積は底辺ADとして高さが同じ6cmってことなので
点Pがどこにあっても、△\(APD\)の面積は\(6×6×\frac{1}{2}=18\)\(cm^2\)となって
△\(APD\)以外の面積\(y=36-18=18\)\(cm^2\)になるってことですね。

\(x\)の値に関係なく、\(y\)の値が決まっているグラフになるので
\(x\)軸に平行になるってことですね。
これもさっきと同じで、6分後には点Cと重なるので、グラフとしては\(x=6\)までの
グラフになるってことですね。
最後に点Cから点Dを点Pが移動した時を見ていきましょう。
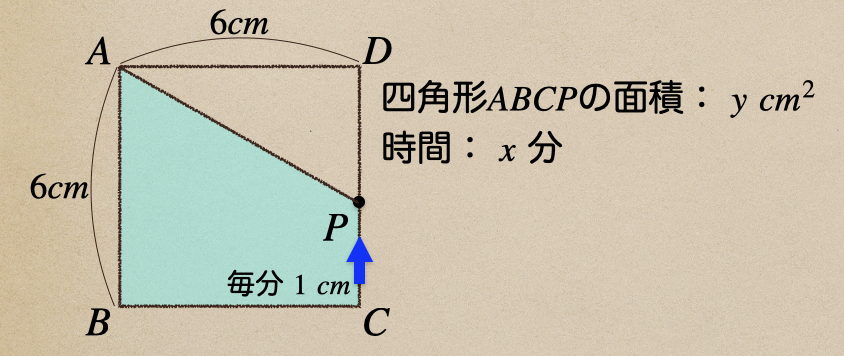
考え方は同じで、四角形\(ABCP\)の面積をどのように求めるかってことですね。
今までは、四角形\(ABCD\)の面積から△\(APD\)の面積をひいていたけど
今回は、四角形\(ABCP\)の面積をそのまま求める方が、計算式が簡単になるので
四角形\(ABCP\)を求めていきますね。
四角形\(ABCP\)は台形になるので『(上辺+底辺)×\(\frac{1}{2}\)×高さ』で求めることが
できるので、\(y=(x+6)×\frac{1}{2}×6=3x+18\)となるってことですね。

グラフも変域\(0≦x≦6\)になっているってことですね。
こんな風に図形の問題はいろいろな状態での変化を1次関数の式にしたりグラフにしたり
するってことなんですね。
今回は、ポイントごとにそれぞれで面積の変化を見ていったんだけど
問題なんかだと『点Aから点Bを通って点Cまで移動した場合』みたいに
面積の変化を組み合わせて考えていかないといけないこともあるよ。
その場合は、今回の解説のように一つ一つのポイントで面積が
どうなっているかっていうのを考えていこう。
(3)速さと1次関数
最後に速さと1次関数っていうことろを見ていきますね。
この速さと1次関数では、時間と道のりの関係を式に表すっていうのが
ポイントになっていて。。

この関係式になるんだね、この速さっていうところがグラフの傾きを表しているんだね。
この関係式を1次関数で表すとどうなるかっていうと。。
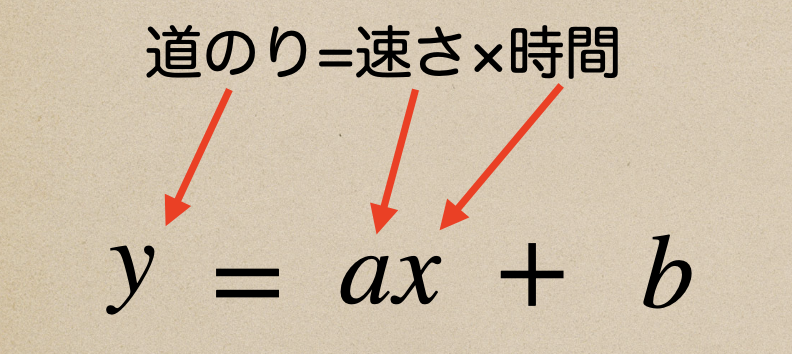
この\(a\)にあたる部分が速さになるってことだね。
じゃあ、この速さが早い時、遅い時っていうのがグラフに
どのように表されるのかっていうのを見てみよう。
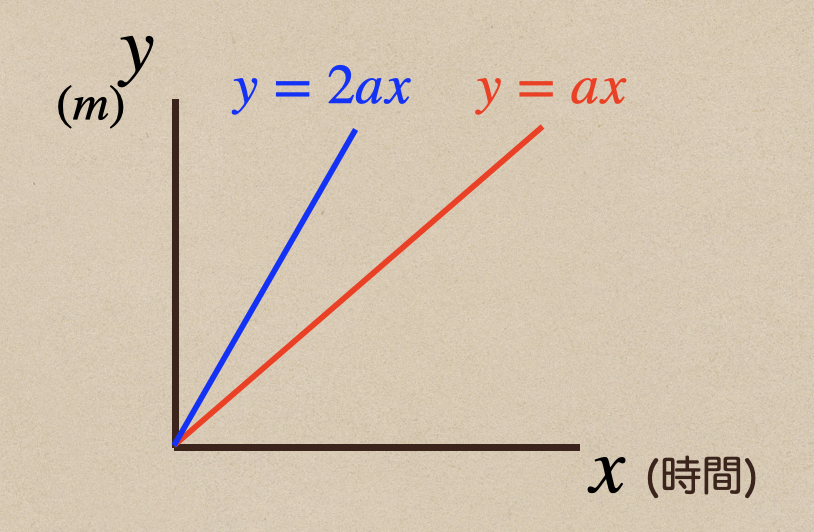
\(y=ax\)と\(y=2ax\)のグラフがあったとき
\(a\)と\(2a\)が速さを表しているんだけど、速さでいうと
\(2a\)の方が、\(a\)より2倍早いってことになりますよね。
それをグラフで表しているのが上の図になっていて、\(a\)より早い\(2a\)の方が
グラフのこう配(傾き)がキツくになっているよね。このことから速さが早いほど
こう配(傾き)がキツくなっているってことなんだね。
逆に速さが遅くなればなるほど、こう配(傾き)はゆるやかになっていくってことだね。
どんどん速さが小さくなって最後には、速さが0になった時っていうのはどうなるかっていうと
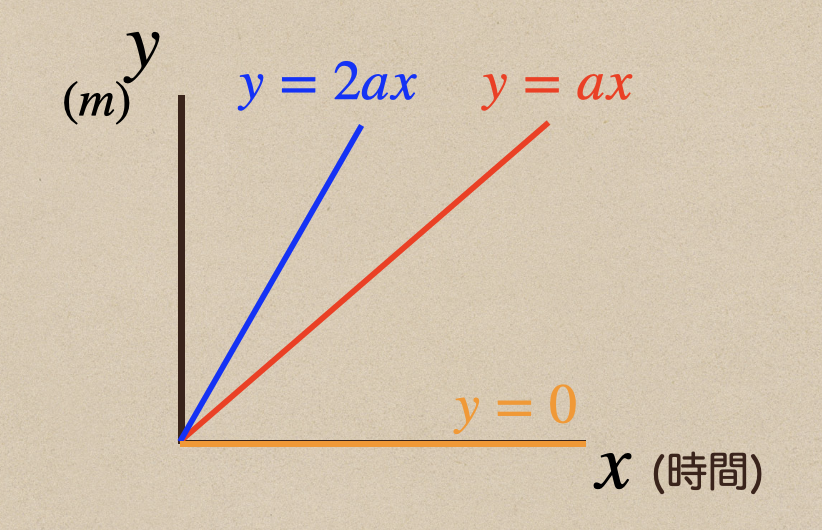
速さが0、ようするに\(a=0\)となるので、\(y=0\)ってことになって
グラフとしては、\(x\)軸上を通るってことになるんだね。
この速さの1次関数っていうのは、この早い、遅い、止まっているっていうものの組み合わせで
問題が出題されることになるんだね。
例えは、今回、解説した組み合わせだと。
・毎時\(a\)\(m\)で出発
・途中で休憩した
・その後、毎時\(2a\)\(m\)で走った
この場合を、グラフにして表すと。。

こんなグラフをひくことができるんだね。
それぞれの色のグラフによって、1次関数の式は異なってくるので
そこもしっかり理解しておこう。特に\(y=2ax+b\)のところは
赤色のグラフと違って、原点を通らないグラフになるってことなので
切片\(b\)が書かれているってことになるんだね。
間違って、\(y=2ax\)としないように注意しておこう。
また、こんなグラフの組み合わせの場合っていうのは、それぞれのグラフで
変域があることになるんだね。

この変域っていうのは、速さと1次関数だけではなく
グラフの中に複数の1次関数の式が混ざっている場合には
この変域っていうのは、存在することになるので覚えておいてください。
今回は、ここまでになります。
ここまでの記事が良かったと思ったらここをクリックしてね。
質問なんかがあった場合はコメントにお願いします。
では、またさようなら



コメント