どうも、こんにちはDKです。
ここでは、中学生で習う数学の基礎を解説しているよ。
今回は中学2年生で習う、『三角形と四角形』の続きで「四角形」についてやっています。
小学校から習ってきた当たり前の図形である三角形をここまでに習ってきた
証明を用いて、この三角形はこんなことが言えるよってことを正しく理解しておこう。
これから学ぶ人は予習として、一度、学んだことのある人は復習に
活用してみてください。
動画でも基礎の解説を行なっているので、そちらも見てみて下さい
(動画は音が出るので注意して)
では、早速初めていきますね。
(1)平行四辺形の性質
この「四角形」の解説では、平行四辺形について考えていきますね。
その前に、四角形では辺や角に呼び名があるのでまずはそれを確認しておきましょう。
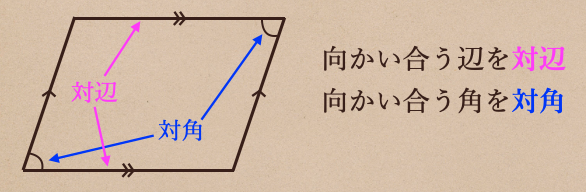
四角形で向かい合う辺を対辺(たいへん)、向かい合う角のことを対角(たいかく)って言うので
これは、どんな四角形に対しても同じ言い方になるよ。
この対辺と対角を説明した図形の形っていうのが平行四辺形になるんだけど
これっていうのが、向かい合う辺が平行になっている四角形ってことで
平行四辺形って言うんだったよね。
二等辺三角形の時のように、平行四辺形の定義を言うと。。
【平行四辺形の定義】
定義:2組の対辺がそれぞれ平行な四角形を平行四辺形と言う
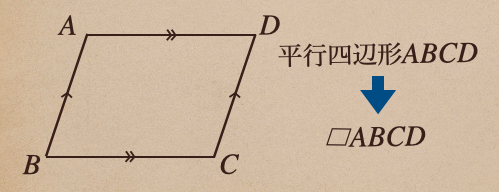
それと、数学では平行四辺形\(ABCD\)があった場合、この平行四辺形を記号で「 □ 」と書いて
□\(ABCD\)って書くこともできるので覚えておこう。
この平行四辺形の性質として
性質①:平行四辺形の2組の対辺はそれぞれ等しい
性質②:平行四辺形の2組の対角はそれぞれ等しい
性質③:平行四辺形の2つの対角線はそれぞれの中点で交わる
これは、小学生で平行四辺形を学んだ時にも習ってきたと思うんだけど
この性質①から③って言うのが本当に成り立つのかって言うのを
平行四辺形の定義から証明してみよう。
[性質①の証明]
「平行四辺形の2組の対辺がそれぞれ等しい」ことを証明するってことなので
まずは、平行四辺形の中から対辺が対応する三角形っていうのを作ってあげて
その三角形が合同であることを証明できれば、対辺が等しいってことを
証明できるよね。なので、
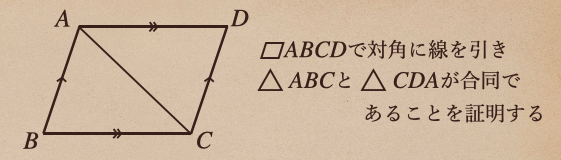
\(\bigtriangleup ABC\)と\(\bigtriangleup CDA\)の対応する辺っていうのは
□\(ABCD\)のそれぞれの対辺ってことになってるよね。
この証明をするにあたって、仮定を言っておくと
仮定:\(AB/\!/ CD\)、\(BC/\!/ AD\)
ってことになるね。 これを証明していくと。。
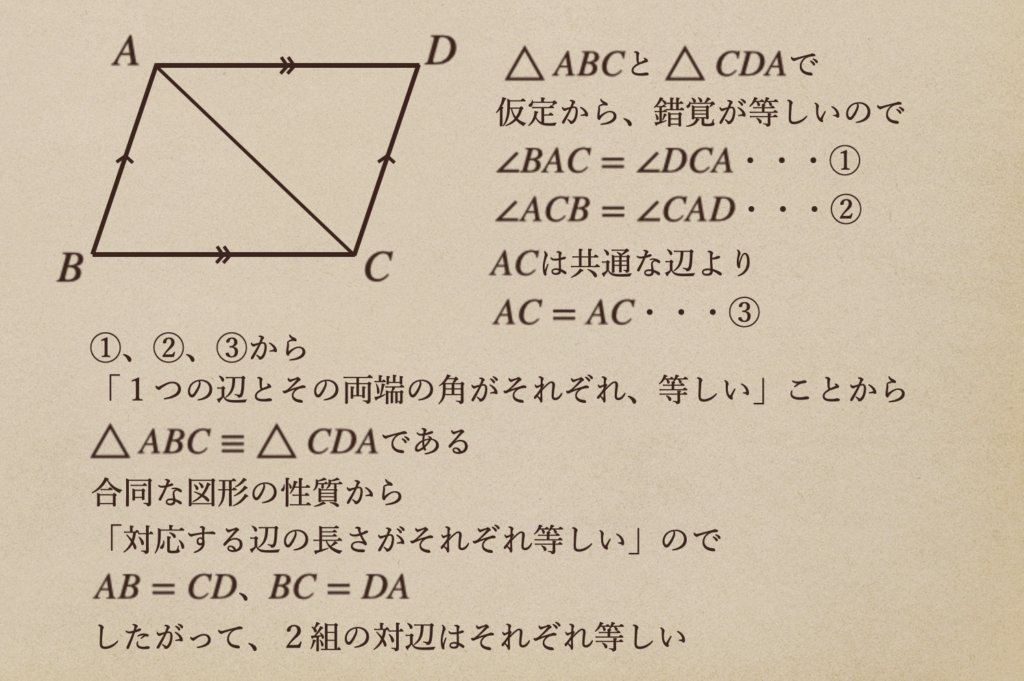
\(\bigtriangleup ABC\)と\(\bigtriangleup CDA\)が合同ってことが言えて
\(AB=CD\)、\(BC=DA\)ってことが証明できたので一つ目の性質であった
「平行四辺形の2組の対辺がそれぞれ等しい」ってことが言えたってことになるんですね。
【性質②の証明】
次は性質②の「平行四辺形の2組の対角はそれぞれ等しい」ことの証明を行っていきましょう。
性質①の証明で\(\angle BAC=\angle DCA\)と\(\angle ACB=\angle CAD\)で
それっていうのが。。
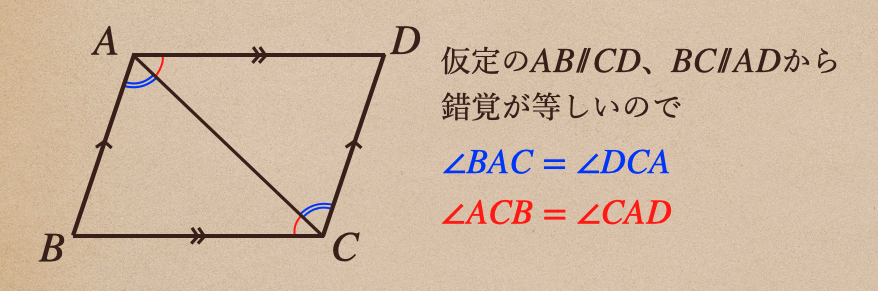
それぞれの角を色をつけて表すと、こういうことになるよね。
ここから\(\angle BAD\)と\(\angle DCB\)を求めてあげるってなると
\(\angle BAD=\)\(\angle BAC\)+\(\angle CAD\)
\(\angle DCB=\)\(\angle DCA\)+\(\angle ACB\)
として書くことができるよね。
そして、この青字の角どうしは等しく、赤字の角どうしは等しいってことなので
\(\angle BAC\)+\(\angle CAD\)=\(\angle DCA\)+\(\angle ACB\)
なので、\(\angle BAD=\angle DCB\)…④ってことが言えて
\(\angle ABC\)と\(\angle CDA\)は\(\bigtriangleup ABC\)と\(\bigtriangleup CDA\)が合同ってことから
合同な図形の性質の「対応する角はそれぞれ等しい」ことから
\(\angle ABC=\angle CDA\)…⑤ってことも言えると
④、⑤から平行四辺形の対角が等しいってことが証明できたね。
【性質③の証明】
「平行四辺形の2つの対角線はそれぞれの中心で交わる」ことの証明ってことだね。
これを図で書き表すと。。
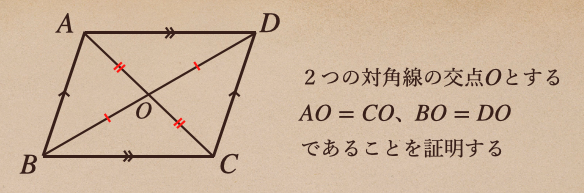
これを証明してあげれば、性質③の証明ができるってことだね。
ここでも、三角形の合同を使って証明していくんだけど、今回は三角形が4つあって
合同となる三角形は\(\bigtriangleup AOD\)と\(\bigtriangleup COB\)、\(\bigtriangleup AOB\)と\(\bigtriangleup COD\)の
どちらかを合同であることを証明できれば\(AO=CO\)、\(BO=DO\)を証明することが
できるんですね。今回は\(\bigtriangleup AOD\)と\(\bigtriangleup COB\)で証明していきますね。
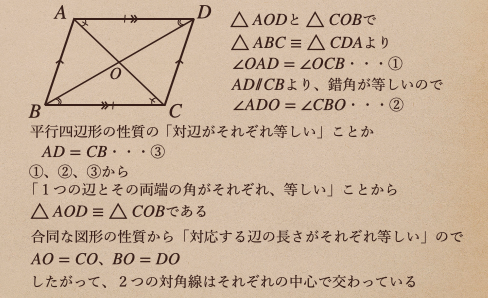
これで、性質①から③までがちゃんと成り立っているってことが証明できましたね。
これを平行四辺形の性質ってことになるので、もう一度確認しておきますね。
【平行四辺形の性質】
定理 1:平行四辺形の2組の対辺はそれぞれ等しい
定理 2:平行四辺形の2組の対角はそれぞれ等しい
定理 3:平行四辺形の2つの対角線はそれぞれの中心で交わる
この平行四辺形の性質はこれからの数学ではよく使うものとなるので
しっかり、理解しておくようにしましょう
(2)平行四辺形であるための条件
一つ前のところで、平行四辺形の定理がわかってもらえたかと思うんだけど
今度は、その定理の逆から四角形を見た時、それは平行四辺形と言えるのかっていうのを
見ていってみましょう。
定理の逆っていうのはそれぞれ
1.2組の対辺がそれぞれ等しい四角形
2.2組の対角がそれぞれ等しい四角形
3.2つの対角線がそれぞれの中点で交わる四角形
この3つになりますね。この3つの四角形は、この時点で平行四辺形ってことは
言えていない、ようするに対辺は平行ですよってことがわかっていない四角形なので
ここで、見ていくのは上の3つの四角形であれば、対辺が平行ですってことが証明できれば
その四角形は平行四辺形ですってことが言えるってことになるんですね。
一つずつ見てみましょう。
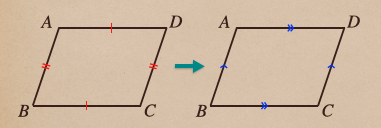
1.2組の対辺がそれぞれ等しい四角形
平行四辺形であるためには、対辺が平行である必要があるので
それを結論として、証明を行なっていくと。。
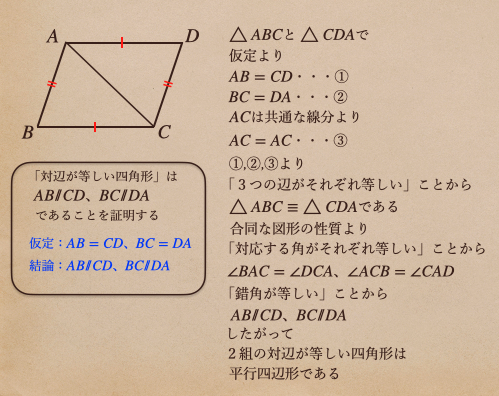
これで、対辺が平行ってことが証明されて、この四角形っていうのは
平行四辺形ですってことが証明されたってことですね。
これで、2組の対辺が等しい四角形っていうのは、平行四辺形であるための
条件ですってことが証明されたんですめね。
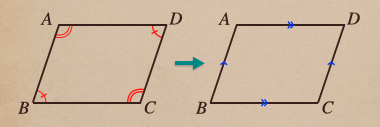
2.2組の対角がそれぞれ等しい四角形
今度は、2組の対角がそれぞれ等しい四角形ならば、平行四辺形であることを
証明していくってことですね。
これを証明するために一つ、補助線を引いてあげてBCとCDの延長線を引いて
その先に点E、点Fとしてあげよう。
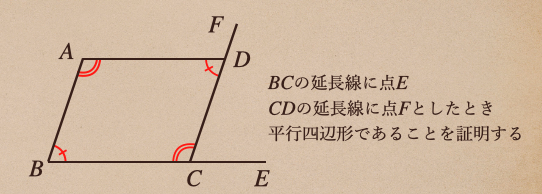
平行四辺形であることを証明しようと思うと、対辺が平行であることを
証明できれば、その四角形は平行四辺形ってことが言えますよね。
なので、この場合の証明は。。
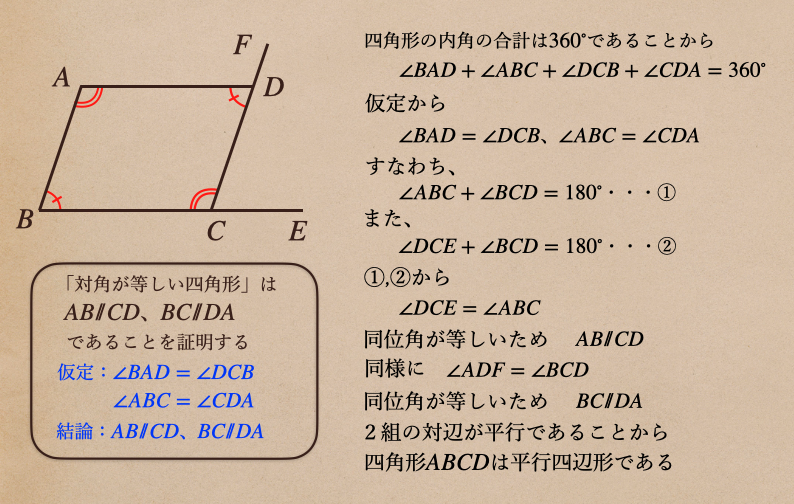
これで、2組の対角がそれぞれ等しい四角形は平行四辺形ってことが言えたね。
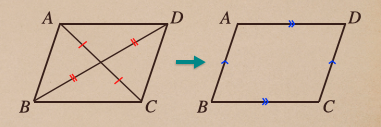
3.2つの対角線がそれぞれの中点で交わる四角形
ここでも、平行四辺形であることを証明していくってことなので、平行線の性質を使って
証明してあげていけばいいってことだね。
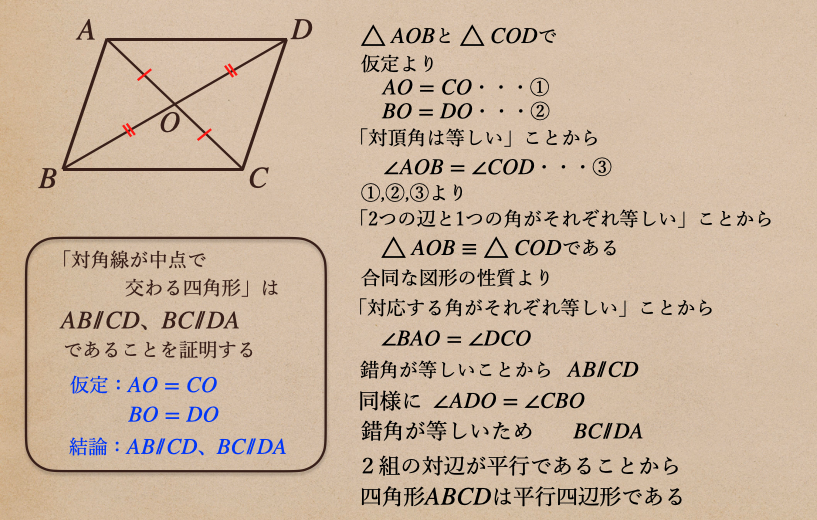
この証明で、対角線が中点でそれぞれ交わる四角形っていうのは
平行四辺形になりますよってことになるんだね。
これで、平行四辺形の性質の逆であっても、平行四辺形ですってことが言えるってことが
わかったね。この3つは平行四辺形であるための条件とも言えるんだね。
平行四辺形であるための条件っていうのが、他にもあって、それっていうのが
1組の対辺が平行で等しい場合になるんだね。
これが本当に平行四辺形になるのかっていうのを確認してみよう。
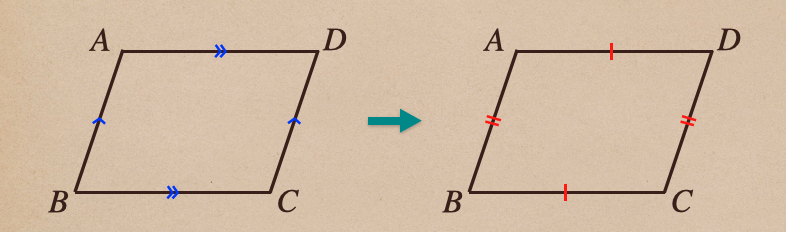
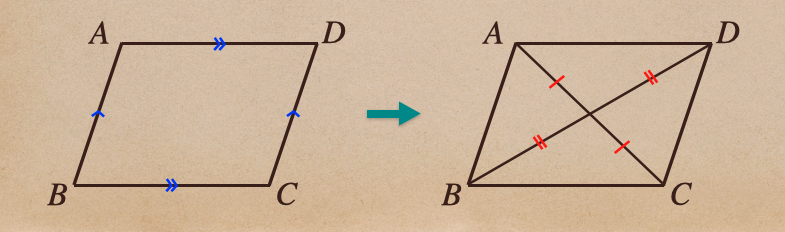
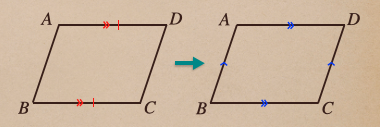
4.1組の対辺が平行で等しい
これっていうのは、図で表すとこういうことだね。。
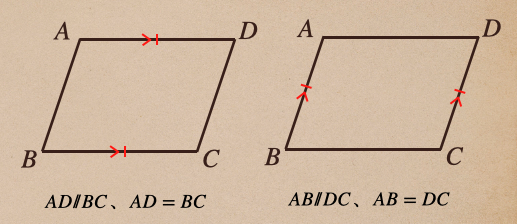
2つの図のどちらかであればそれは、平行四辺形ってことになるってことだね、
これが本当に平行四辺形になるのか、証明して確認してみるね。
証明は上の図の左側の\(AD/\!/BC,AD=BC\)で見ていきますね。
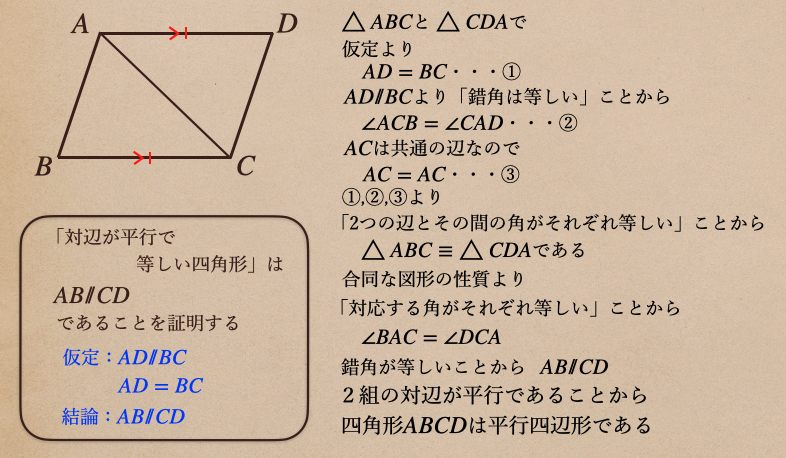
今回の証明では、すでに\(AD/\!/BC\)であることは仮定として言われているので
証明すべきは、\(AB/\!/CD\)ってことですね。これが証明できたので
2組の対辺がそれぞれ平行ってことで、この四角形は平行四辺形ですってことが
証明されましたね。
平行四辺形であるための条件っていうのは全部で、この4つになっておさらいすると
【平行四辺形であるための条件】
定理:四角形は、次のどれかが成り立っているとき、
平行四辺形である
1:2組の対辺がそれぞれ等しい
2:2組の対角がそれぞれ等しい
3:2つの対角線がそれぞれ中点で交わる
4:1組の対辺が平行で等しい
この内容は、覚えておこう。
ただ、覚えるのではなくて、今回、行なったようにそれぞれが平行四辺形であることを
確認した証明の内容っていうのも理解した上で覚えておくようにしよう。
(3)特別な平行四辺形
平行四辺形の定義や性質っていうのを理解してもらえたかなと思うんだけど
ここでは、『ひし形』、『長方形』、『正方形』と平行四辺形の関係について
考えていきますね。

この『ひし形』、『長方形』、『正方形』にもそれぞれ定義があってそれっていうのが。。
【ひし形の定義】4つの辺が等しい四角形をひし形と言う
【長方形の定義】4つの角が等しい四角形を長方形と言う
【正方形の定義】4つの辺が等しく、4つの角が等しい四角形を正方形と言う
これが、定義になるんだね。言われてみればそうなっているなってことが
定義として定められているんだね。
じゃあ、これらが平行四辺形との関係を見た時に、それぞれの定義からこんな証明をすることが
できるんだね。
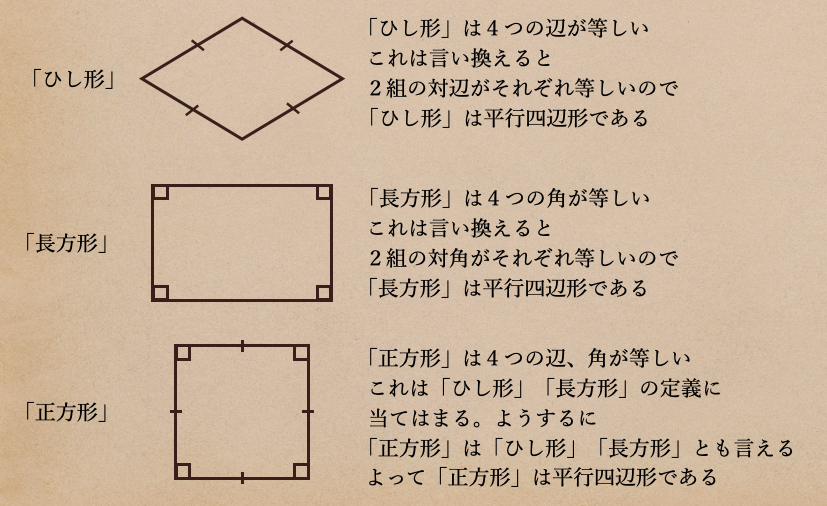
「ひし形」「長方形」「正方形」はすべて平行四辺形ってことがわかるよね。
これって言うのは
ひし形、長方形、正方形は、平行四辺形の特別なものである
ってことになるんだね。
「平行四辺形」「ひし形」「長方形」「正方形」の関係を図で表すと。。
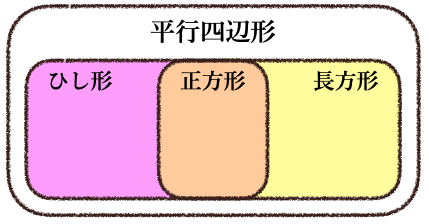
「ひし形」「長方形」「正方形」すべて、平行四辺形に含まれていて
「正方形」は「ひし形」にも「長方形」にも含まれている四角形ってことになるんだね。
今度は、「平行四辺形」「ひし形」「長方形」「正方形」でそれぞれに対角線を引いて
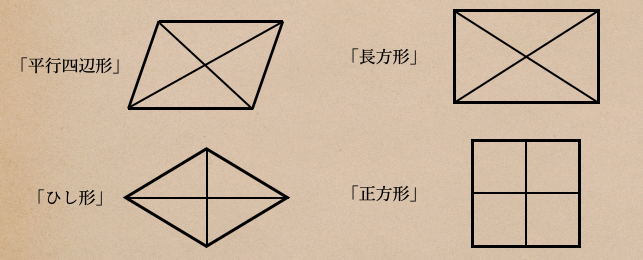
この、引かれた対角線っていうのが
・それぞれの中点で交わっている
・垂直に交わっている
・2つの対角線の長さが等しい
どの四角形が上の項目のどれに当てはまるのかって言うのを見てみましょう。
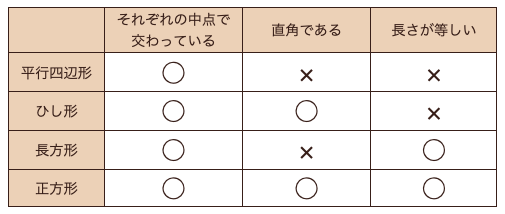
この表から「ひし形」「長方形」「正方形」はすべて、平行四辺形ってことなので
平行四辺形の対角線の性質である、中点で交わるって言うのは
すべてに当てはまるってことだね。
それぞれの四角形には、他にも特徴があってそれっていうのが
【ひし形、長方形、正方形の対角線の性質】
ひし形の対角線が垂直に交わる
長方形の対角線は長さが等しい
正方形の対角線は垂直に交わり、長さが等しい
ってことになるんだね。
それぞれ四角形で定義、性質って言うのを持っているので
どの四角形がどうかって言うのを、しっかり理解しておくようにしていこう。
(4)平行線と面積
平行な2直線mとnがあってそこに2つの三角形があるとき
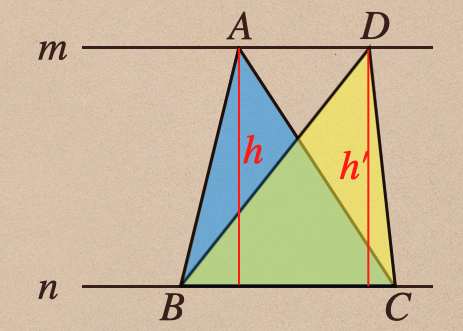
\(\bigtriangleup ABC\)と\(\bigtriangleup DBC\)では底辺が共通で\(BC\)となっていて
高さは、それぞれ、\(h\)、\(h’\)して、平行な2直線の垂線となっているので
\(h=h’\)と高さは、等しいってことだね。
\(\bigtriangleup ABC\)と\(\bigtriangleup DBC\)の面積を求めようとしたら
底辺が同じで高さも同じってことなので、この2つの三角形は面積が等しいってことですね。
こんな風に、面積が同じ三角形を\(\bigtriangleup ABC=\bigtriangleup DBC\)として
書いて表すことができるんだね。
こんな風に、平行線上に引かれた三角形っていうのは底辺が同じであれば
面積は同じになるってことなんだね。
今回は、ここまでになります。
ここまでの記事が良かったと思ったらここをクリックしてね。
質問なんかがあった場合はコメントにお願いします。
では、またさようなら




コメント