どうも、こんにちはDKです。
今回は中学3年生で習う「2次方程式」について基礎をやっていきますね。
2次方程式って何?ってところから、方程式ってことなので、そこには解があるので
その解の求め方についてここで、解説していきますね。
この2次方程式の解き方の中には、平方根を利用するところもあるので
平方根について、まだまだ、理解が足りないなって人は ここ から
平方根を復習していこう。
[1]2次方程式とその解
2次方程式について考えていこう。
2次方程式っていうのは、言葉の通り「2次」の「方程式」ってことだね。

「方程式」っていうと、中学1年生の時に習ったもので簡単に言うと
「文字と数字で両辺が等しくなっている等式」のことだったよね。
そして、「2次」はって言うとこれは次数が2ってことを指しているんだね。
次数っていうのは、「文字式の項を掛け合わされている文字の個数」のことを言っていて
その、次数が2ってことなので、2つの文字がかけ合わされているってことになるね。

これらをふまえて、2次方程式を説明すると。。
2次方程式
2次の項をふくむ等式で、すべての項を左辺に移行して
左辺が文字の2次式になる方程式
つまり・・\(ax^2+bx+c=0\) (\(a\)、\(b\)、\(c\)は定数。\(a≠0\))
の形になる方程式を\(x\)についての「2次方程式」という
ってことなんだね。
そして、この2次方程式を成り立たせる文字の値を、その2次方程式の解(かい)と言って
すべての解を求めることを、その2次方程式を解く(とく)って言うんだね。
例えば。。
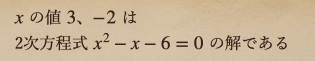
こんな言い方をしてあげて、この2次方程式の解っていうのは、その\(x\)の値を
代入してあげると、等式が成り立っているってことになるんだね。
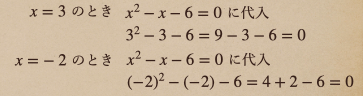
これで、2次方程式がなんなのかって言うのはわかってもらえたかと思うので
次からは、2次方程式の解き方っていうのを解説していくよ。
[2] 因数分解による2次方程式の解き方
ここからは、2次方程式の解き方について解説していきますね。
まずは、タイトルにもあるように因数分解を使って、2次方程式を解いていくってことなんだけど
例えば、\(x^2-6x+8\)を因数分解したら。。\((x-4)(x-2)\)となりますよね?

じゃあ、2次方程式 \(x^2-6x+8=0\)があった場合、これっていうのは左辺を因数分解して
\((x-4)(x-2)=0\)とすることができますよね。
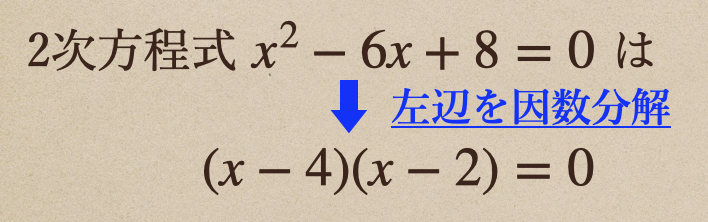
そんでもって、\((x-4)(x-2)=0\)っていうことは、\((x-4)=0\)もしくは\((x-2)=0\)となれば
\((x-4)(x-2)=0\)が成り立ちますよってことが言えますよね。
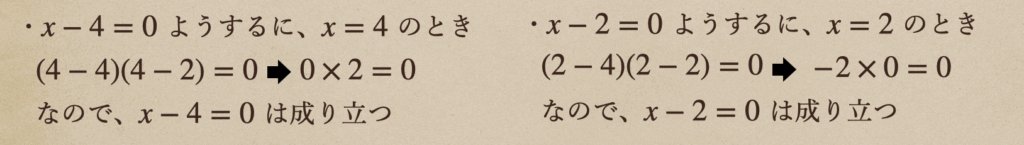
ちなみに、\(x=4\) や \(x=2\) 以外の場合も見ていると。。
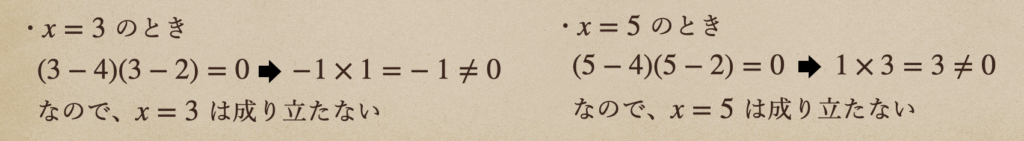
となって、これっていうのは\((x-4)(x-2)=0\) を成り立たせるには\(x=4\) 、\(x=2\)だけとなって
それ以外にはないってことになるんだね。
ようするに、『2つの数や式が\(A\)や\(B\)として見たとき
\(AB=0\)ならば、\(A=0\)または\(B=0\)となる』
これを利用すると、因数分解を使って2次方程式を解くことができるってことになるんですね。
次に因数分解って、4つの公式があったと思うんだけど、それぞれで2次方程式の解を
求めてみますね。
(1) 2次方程式 \((x+a)(x+b)=0\) の解き方
これは冒頭でも、説明したんですけど2次方程式\(x^2+(a+b)x+ab=0\) の形になっている式で
これっていうのは左辺を因数分解すると \((x+a)(x+b)=0\) となるので
\(x+a=0\)または\(x+b=0\) としてみることができて、ようするに\(x=-a\)、\(x=-b\)と
なりますよってことで、2次方程式の解を求めることができるんですね。

このパターンの例題を見ていきますね。
[ 例題1 ]\(x^2+3x-18=0\)
➡︎ \((x+6)(x-2)=0\)
➡︎\(x+6=0\) または \(x-2=0\)
➡︎よって、\(x=-6\)、\(x=2\)
\(x+6=0\) または \(x+2=0\)として考えてあげれば、移行して\(x=-6\)、\(x=2\)とするだけで
解を求めることができるんだけど、慣れてないくれば、そのまま\((x+6)(x-2=0\)から
解を求めていくことができるんだけど、その場合は因数分解したときのカッコの中の数と
2次方程式の解の数っていうのは符号が変わってくるので、そこは注意しておくようにしよう。
(2) 2次方程式 \((x+a)^2=0\)、\((x-a)^2=0\) の解き方
因数分解の公式の2つ目\(x^2+2ax+a^2=(x+a)^2\)、3つ目\(x^2-2ax+a^2=(x-a)^2\)の
形になっている2次方程式の解き方についてやっていくね。
この2つ目と3つ目の場合は、それぞれ、\(x+a=0\)と\(x-a=0\)になるので
2次方程式\(x^2+2ax+a^2=0\)は\((x+a)^2=0\)となって、解は\(x=-a\)となって
2次方程式\(x^2-2ax+a^2=0\)は\((x-a)^2=0\)となって、解は\(x=a\)となるんだね。
この2つ目、3つ目のパターンの2次方程式は解が1つになるんだね。

このパターンの例題を見ていきますね。まずは、2つ目のパターン。。
[ 例題 2]\(x^2+10x+25=0\)
➡︎ \((x+5)^2=0\)
➡︎\(x+5=0\)
➡︎よって、\(x=-5\)
3つ目のパターンの例題は。。
[ 例題 3]\(x^2-18x+81=0\)
➡︎ \((x-9)^2=0\)
➡︎\(x-9=0\)
➡︎よって、\(x=9\)
(3) 2次方程式 \((x+a)(x-a)=0\)の解き方
因数分解の公式の4つ目\(x^2-a^2=(x+a)(x-a)\)の形になっている2次方程式の
解き方についてやっていきますね。
この4つ目の場合は、それぞれ、\(x+a=0\)と\(x-a=0\)になるので
2次方程式\(x^2-a^2=0\)は\((x+a)(x-a)=0\)となって、解は\(x=-a\)と\(x=a\)となるんだね。

このパターンでの例題をやってみますね。
[ 例題 4]\(x^2-16=0\)
➡︎ \((x+4)(x-4)=0\)
➡︎\(x+4=0\)または\(x-4=0\)
➡︎よって、\(x=-4\)、\(x=4\)
これらが、因数分解の公式を利用した2次方程式の解の求め方になりますね。
他にも、因数分解を利用して解く方法っていうのがあので、それも紹介しておきますね。
(4)共通因数をくくり出して2次方程式の解き方
\(x^2+ax=0\)の型の場合、これは、共通因数である「\(x\)」をくくり出して
因数分解してあげて、\(x(x+a)=0\)とすることができて、\(x=0\)または\(x+a=0\)から
\(x=0\)または\(x=-a\)が答えになるってことでなんですね。

これも、例題を解いていきますね。
[ 例題 5]\(x^2+5x=0\)
➡︎ \(x(x+5)=0\)
➡︎\(x=0\)または\(x+5=0\)
➡︎よって、\(x=0\)、\(x=-5\)
(5)式を整理して因数分解する2次方程式の解き方
これは、\((x+a)(x+b)=c\)の型で右辺が「\(0\)」ではなく「\(c\)」になっているね。
こう言った型の2次方程式の場合は、まず、右辺が「\(0\)」になるように
式を整理してあげて、\((x+d)(x+e)=0\)の型にしてあげることで2次方程式の解を
求めていくことができるってことになるんだね。
[ 例題 6]\((x+4)(x-2)=-5\)
➡︎ \(x^2+2x-8=-5\)
➡︎ \(x^2+2x-3=0\)
➡︎ \((x+3)(x-1)=0\)
➡︎\(x+3=0\)または\(x-1=0\)
➡︎よって、\(x=-3\)、\(x=1\)
こんな風に、2次方程式の左辺を因数分解してあげて2次方程式の解を求めていってあげる
解き方になりますね。
ここでの注意としては、左辺が多項式および単行式の積の型にしてあげることが
できる場合に限って、使っていくことができるものになりますね。
次の項では、因数分解が行えない2次方程式についてやっていきますね。
[3]平方根の考えを使った2次方程式の解き方
平方根の考えを使った2次方程式の解き方について解説していくね。
平方根っていうのは、「\(2\)の平方根は\(\sqrt{2}\)」っていうのを利用するってことになるんだね。
ようするにどういうことかと言うと、\(x^2=4\)っていう場合は、\(4\)を\(2^2\)にしてあげて
\(x^2=2^2\)として考えてあげると、左辺も右辺も2乗をなくしてあげて\(x=2\)となるよね。
これで\(x\)の値が求められたってことになるんだね。
ただ、\(x^2=4\)の場合は\(x^2=(-2)^2\)とすることもできるので、\(x=-2\)でもあるってことなので
\(x^2=4\)の\(x\)の値は\(x=±2\)ってことになるよ。
これを利用して次のパターンの解き方っていうのを見ていってみよう。
(1) \(ax^2-c=0\)の形
こう言った形の場合の解き方は。。

こんな風に、平方根を利用して、\(x\)の値を求めてあげるってことになるんだね。
具体的に例題を解いてみよう。
[ 例題 1] \(3x^2-12=0\)
➡︎ \(3x^2=12\)
➡︎ \(x^2=4\)
➡︎ \(x^2=(±2)^2\)
➡︎ \(x=±2\)
これで、\(x\)の値を求めることができるんだね。
今回の例題では右辺の数の項が平方根が整数になる問題だったので
\(x\)の値も整数になったってことだね。
注意としては、平方根で表すときっていうのは、正の数も負の数の両方を
解として表してあげないといけないんだね。
あともう1つ注意があって、それは右辺の数の項っていうのは負の符号になっていなことが
大切で負の符号であった場合、根号で表すことができないってことになるんだね。
(2) \((x+m)^2=n\)の形
今度は\((x+m)^2=n\) の形の場合を見ていきますね。
これっていうのは、両辺を2乗の形にしてから、その2乗をなくしてあげて
\(x\)を求めてあげるっていうやり方になりますね。
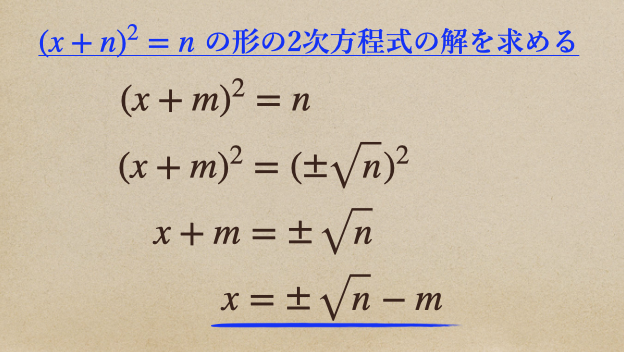
これを踏まえて例題をやってみましょう。
[ 例題 2 ]\((x-2)^2=6\)
➡︎\((x-2)^2=(±\sqrt{6})^2\)
➡︎\(x-2=±\sqrt{6}\)
➡︎\(x=±\sqrt{6}+2\)
ここで、右辺は\(6\)の平方根を求めることになるんだけどその場合
正の符号と負の符号の両方が\(6\)の平方根ってことになるので\(±\sqrt{6}\)となるんだね。
\(±\)っていうのを忘れないようにしよう。
この例題の解は、\(x=±\sqrt{6}+2\)ってことなのでこれっていうのは
\(x=\sqrt{6}+2\)と\(x=-\sqrt{6}+2\)ってことになりますね。
(3) \(x^2+bx=c\)の形
これは、まず式を\((x+m)^2=n\)の形にしてあげてから(2)の解き方で
\(x\)を求めてあげればいいってことになるんですね。

ここは実際に例題で解き方を見てもらった方が、わかりやすいですね。
ちなみに、\(x^2+bx+c=0\)の形にして、因数分解ができるのであれば
因数分解して解いてあげればいいってことになりますね。
[ 例題 3 ]\(x^2+8x=4\)
➡︎\(x^2+8x+16=4+16\)
➡︎\(x^2+8x+16=20\)
➡︎\((x+4)^2=20\)
➡︎\(x+4=±\sqrt{20}\)
➡︎\(x=±\sqrt{20}-4\)
➡︎\(x=±2\sqrt{5}-4\)
この\(x^2+bx=c\)のパターンのポイントとしては左辺を\((x+m)^2\)の形に
してあげる必要があって\((x+m)^2\)の形にするために左辺の\(x^2+bx\)を
「\(x\)の係数の半分を2乗する」数を両辺に足してあげれば左辺を\((x+m)^2\)に
してあげることができるんだね。
さっきの例題3の場合だと。。

「\(x\)の係数の半分を2乗する」数を両辺に足すことをしっかり覚えておこう。
今回の例題3の2次方程式の解き方っていうのは、他にもあって、次のところでは
その解き方について説明していきね。
(4) 2次方程式の解の公式
この2次方程式の解の公式っていうのは、いろいろな2次方程式で使うことができて
今まで説明していた(1)から(3)の問題でも、この2次方程式の解の公式を
使って解くことができるんですね。その公式っていうのが。。
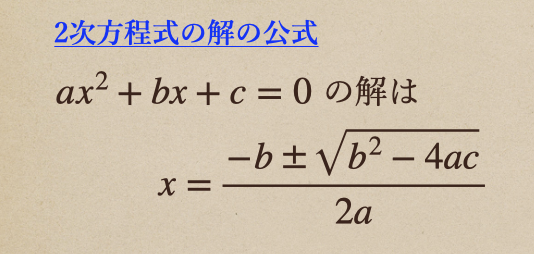
ってことになるんだね。ちょっと、複雑な公式になってはいるんだけど
それぞれの係数の\(a\)、\(b\)、\(c\)を代入してあげれば、\(x\) の値を
求めることができるっってってことなんだね。
ここでの例題は例題1〜3を2次方程式の解の公式を使って解いてみるね。
[例題1]\(3x^2-12=0\)
➡︎\(x^2-4=0\)
\(a=1\)、\(b=0\)、\(c=-4\)を\(\frac{-b±\sqrt{b^2-4ac}}{2a}\)に代入
➡︎\(x=\frac{-0±\sqrt{0^2-4×1×(-4)}}{2×1}\)
➡︎\(x=\frac{±\sqrt{16}}{2}\)
➡︎\(x=\frac{±4}{2}\)
➡︎\(x=±2\)
[例題2]\((x-2)^2=6\)
➡︎\(x^2-4x+4=6\)
➡︎\(x^2-4x-2=0\)
\(a=1\)、\(b=-4\)、\(c=-2\)を\(\frac{-b±\sqrt{b^2-4ac}}{2a}\)に代入
➡︎\(x=\frac{-(-4)±\sqrt{(-4)^2-4×1×(-2)}}{2×1}\)
➡︎\(x=\frac{4±\sqrt{16+8}}{2}\)
➡︎\(x=\frac{4±\sqrt{24}}{2}\)
➡︎\(x=\frac{4±2\sqrt{6}}{2}\)
➡︎\(x=2±\sqrt{6}\)
[例題3]\(x^2+8x=4\)
➡︎(\x^2+8x-4=0\)
\(a=1\)、\(b=8\)、\(c=-4\)を\(\frac{-b±\sqrt{b^2-4ac}}{2a}\)に代入
➡︎\(x=\frac{-8±\sqrt{8^2-4×1×(-4)}}{2×1}\)
➡︎\(x=\frac{-8±\sqrt{64+16}}{2}\)
➡︎\(x=\frac{-8±\sqrt{80}}{2}\)
➡︎\(x=\frac{-8±4\sqrt{5}}{2}\)
➡︎\(x=-4±2\sqrt{5}\)
(1)〜(3)でやった例題の解と今回の2次方程式の解の公式を使って解いた解が
同じ答えとなることが確認できたね。
どっちの解き方で解いても答えは同じになるので、自信がないなって場合は
2次方程式の解の公式を使って、チェックしてみて同じ解になっているのかっていうのを
見てあげることもできるんだね。
ちなみに、この2次方程式の解の公式がなんで\(\frac{-b±\sqrt{b^2-4ac}}{2a}\)なのかって
気にならない?
そういうもんでしょって割り切っちゃうのもいいんだけど、こう言った「公式」には
ちゃんと理由があるんだ。
それをしっかり理解して、この2次方程式の解の公式を覚えていくっていうのは
すごく大事なので、この2次方程式の解の公式がどうやって成り立っているのかっていうのを
確認しておこう。
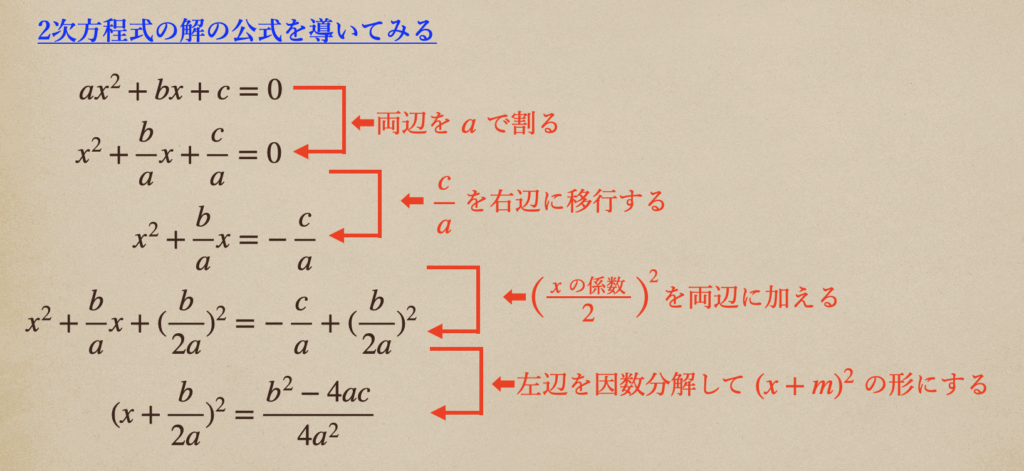
まだ、途中なんだけど\(ax^2+bx+c=0\)を赤字に書かれている通りに式を変形させていって
最終的に\(x\)について解いてあげるんだね。
ここから両辺を2乗の形にしてあげて、2乗をなくしてあげて、\(x=\)の形にして
あげて終わりってことになるね。
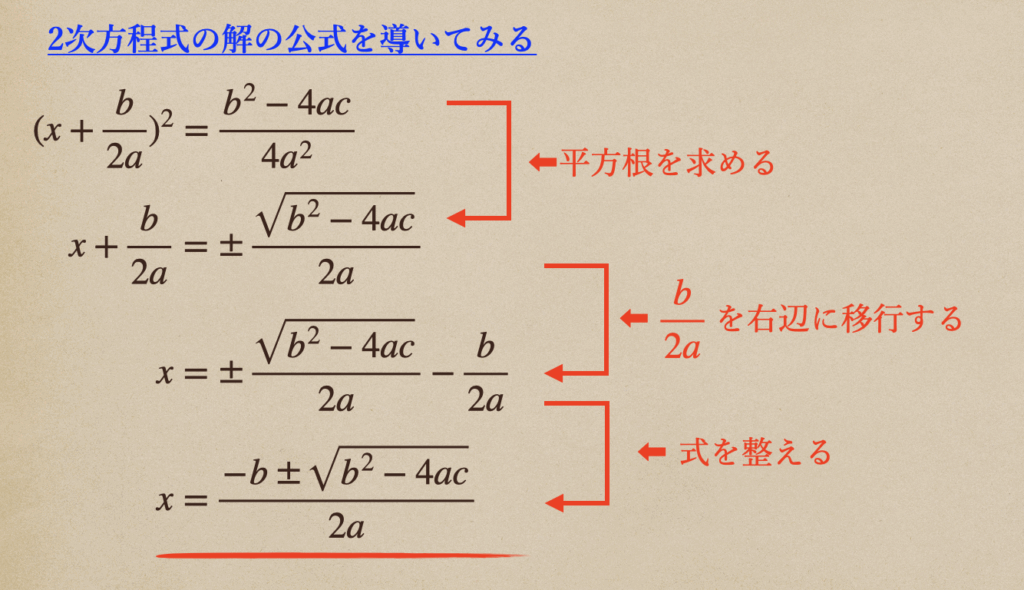
これが2次方程式の解の公式ってことになるんだね。
この解の公式の導き出しっていうのを覚える必要はまったくないんだけど
こんな風にして、2次方程式の解の公式は導き出されたんだよっていうことは
知っておいてもらえたらいいかな。
ここまでで、2次方程式の解き方ってことなんだけど、ここで説明していたように
解き方っていうのにも、いろいろあるってことなんだね。
いざ、2次方程式を解くってなるとどれを利用して解いていけばいいのかっていうので
悩んでしまうこともあると思うんだけど、この2次方程式の解き方では次の
解き方を順に検証していって適切な解き方っていうのを見つけていけるように
していこう。
【2次方程式の解き方の順番】
1. 因数分解を使って解く
2. 平方根の考えを使って解く
3. 解の公式を使って解く
一つ目に、\(ax^2+bx+c=0\)の形で左辺が因数分解できるかどうかっていうのを
見てあげて、ここで因数分解できるようなら、解を求めることはできるよね。
もし、因数分解で解くことができなければ、2つ目の平方根の考えを使って解く方法を
試してみて、これでも解くことができなければ最後に解の公式を使って、\(x\)を
求めてあげれば、2次方程式の解を求めていってあげればいいってことになりますね。
今回は、ここまでになります。
ここまでの記事が良かったと思ったらここをクリックしてね。
質問なんかがあった場合はコメントにお願いします。
では、また、さようなら。



コメント