どうも、こんにちはDKです。
今回は中学3年生で習う相似な図形についてやっていきますね。
相似は「そうじ」っていう読み方をして、これがどういうことなのかっていうのを
ここで、説明していきますね。
この相似っていうのは、中学2年生で習った「合同」っていうのと関わりが
あるんだけど、それは後で説明をしていきますね。
合同っていうのが、どんなモンだったかっていうのを確認したい場合は
ここをクリックしてくれれば、合同に関する解説ページに飛べるよ。
それじゃあ、始めていきますね。
(1) 図形の拡大・縮小と相似
さっそくだけど、次のことについて考えてみよう。
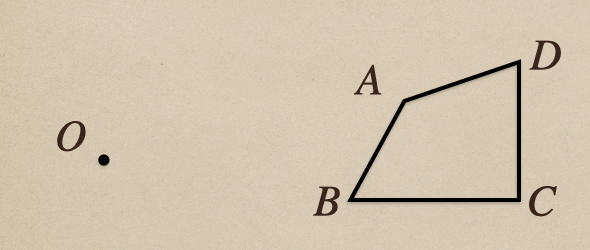
点\(O\)から四角形\(ABCD\)のそれぞれの頂点を通って
\(2OA=OE\)、\(2OB=OF\)、\(2OC=OG\)、\(2OD=OH\)となる点に
\(E\)、\(F\)、\(G\)、\(H\)の点を置く、この点\(E\)、\(F\)、\(G\)、\(H\)を
順に線で結んでできた四角形\(EFGH\)を作ったとき
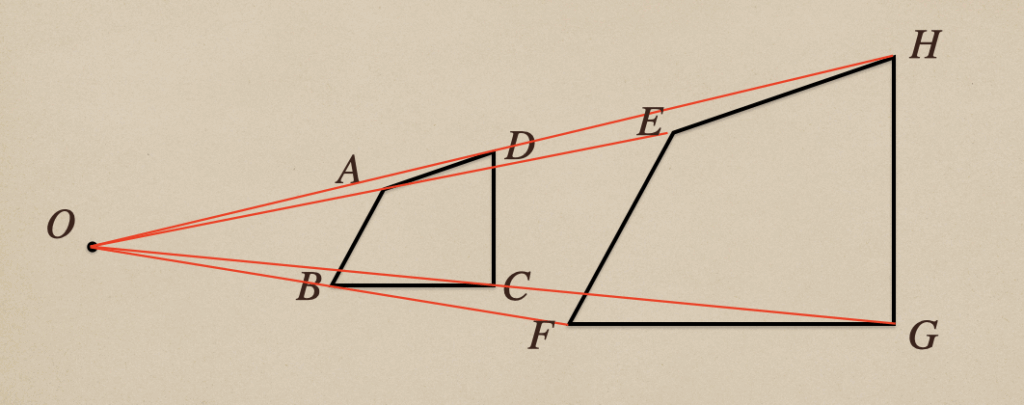
このとき
四角形\(EFGH\)は四角形\(ABCD\)の2倍の拡大図
四角形\(ABCD\)は四角形\(EFGH\)の\(\frac{1}{2}\)の縮図
であるってことになるんだね。
これは
1点\(O\)を決めて、図形を拡大、縮小したときっていうのは
対応する線分の比は点\(O\)から対応する2つの点までの長さに等しくなって
対応する角の大きさはそれぞれ等しくなる
ってことなんだね。
なので、上の四角形\(ABCD\)と四角形\(EFGH\)は2倍(拡大)、\(\frac{1}{2}\)(縮小)の
関係にあるってことは、点\(O\)からの頂点の関係が
\(2OA=OE\)(拡大)、\(OA=\frac{1}{2}OE\)(縮小)で等しいってことを言っていて
対応する角度が等しいっていうのは角\(A\)に対応する角\(E\)は等しいですよってことを
言っているんだね。
このように、図形を拡大、縮小した図形と合同となっている図形は
もとの図形と「相似(そうじ)」であると言う ってことなんだね。
なので、この四角形\(ABCD\)と四角形\(EFGH\)は相似であるってことなんだけど
これを記号『 ∽ 』を使って、[ 四角形\(ABCD\) ∽ 四角形\(EFGH\) ]と表すんだね。
ちなみに、ここで対応する頂点は順に書いてあげる必要があって
これは、「合同」と同じ考え方になるので注意しておこう。
(2) 相似な図形の辺や角
(1)の四角形\(ABCD\)と四角形\(EFGH\)が相似であるってことがわかったんだけど
この2つの四角形の辺や角っていうのがどうなっているのか見てみると
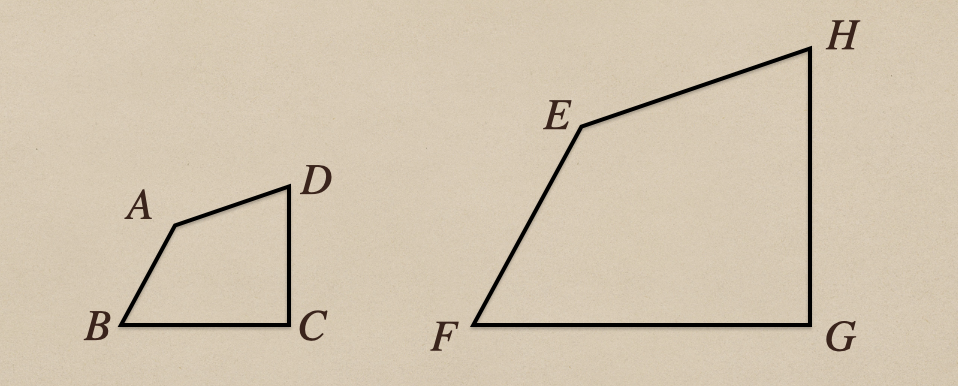
[ 辺 ] \(2AB=EF\)、\(2BC=FG\)、\(2CD=GH\)、\(2DA=HE\)となる
これは、\(AB:EF=BC:FG=CD:GH=DA:HE=1:2\)ってことが言えるんだね。
これは、「対応する線分の比はすべて等しい」ってことなんだね。
[ 角 ] \(\angle{ABC}=\angle{EFG}\)、\(\angle{BCD}=\angle{FGH}\)
\(\angle{CDA}=\angle{GHE}\)、\(\angle{DAB}=\angle{HEF}\)
ってことなんだね。これは「対応する角がそれぞれ等しい」ってことが言えるんだね。
これが、この相似な図形の性質ってことになるんだね。
<相似な図形の性質>
- 対応する線分の比はすべて等しい
- 対応する角はそれぞれ等しい
そして、この相似な図形の対応する線分の比をそれらの図形の相似比と言って
四角形\(ABCD\)と四角形\(EFGH\)の相似比は\(1:2\)になるってことなんだね。
(3) 三角形の相似条件
(2)で説明していたように、相似な図形の性質から三角形の相似っていうのを
考えてあげると、次のようなことが言えるんだ。
①3組の辺の比がすべて等しい
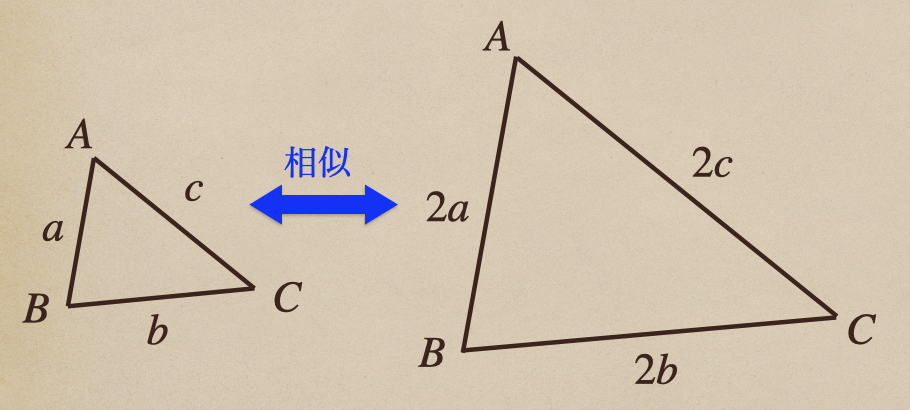
上の三角形は対応する辺の比がすべて\(1:2\)になっているから「相似」ってことだね。
これは、「3組」っていうのがポイントで1組ではもちろん、2組の比が等くても
三角形の相似っていうのは言えないってことなんだね。
もちろん、相似な三角形であれば、1組の比は等しいし、2組の比も等しいってことは
言えるんだけど、2組の比が等しいからといって、それらの三角形が相似であるとは
言い切れないってことなんだね。
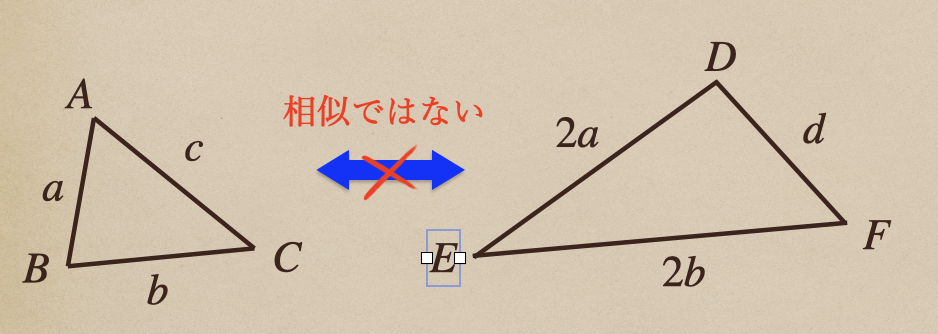
この場合、辺\(AB\)と辺\(DE\)と辺\(BC\)と辺\(EF\)は\(1:2\)の関係になってるけど
辺\(CA\)と辺\(FD\)は\(1:2\)の関係にはなっていないんだけど
2つの三角形は相似ではないよね。こんな風に、2組の辺の比が等くても、それらの三角形は
相似であるとは言えないこともあるってことになるんだね。
3組の辺の比がすべて等しい場合は、必ずそれらの三角形は相似になっているってことが
言えるってことなんだね。
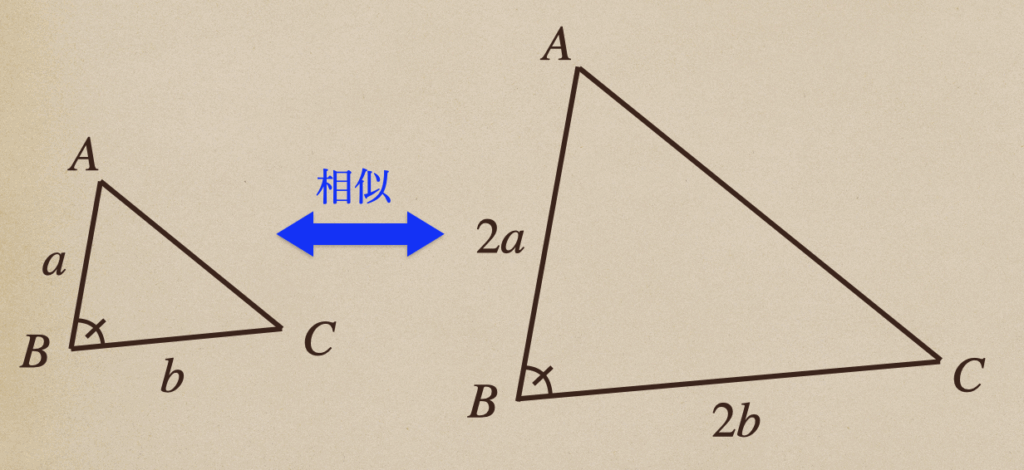
②2組の辺の比が等く、その間の角が等しい
2組の比が等しいだけだと相似にはならないこともあるんだけど、そこに
「その間の角が等しい」っていう条件が加われば、それらの三角形は相似ってことになるんだね。
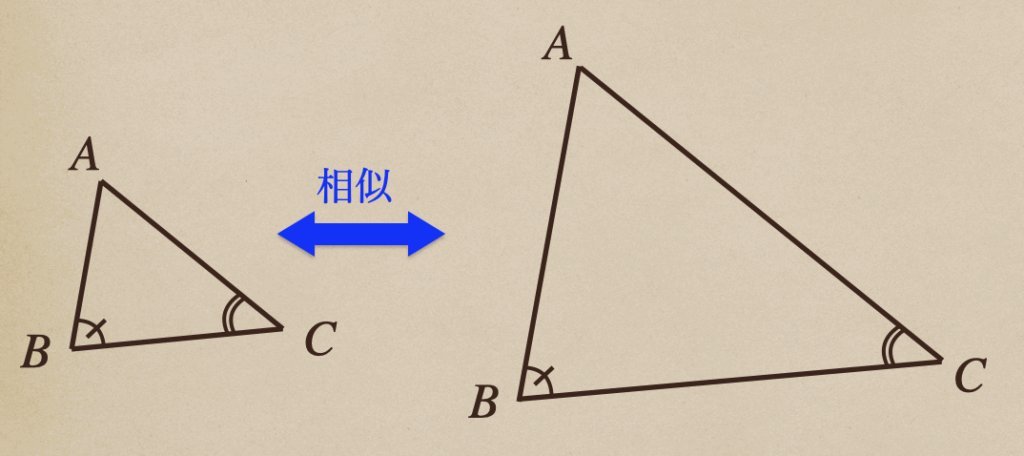
③2組の角がそれぞれ等しい
(2)で説明した「対応する角はそれぞれ等しい」っていう性質を三角形に当てはめて
考えてあげると、三角形っていうのは角が3つで、そのうち2つの角がわかっていれば
残りの核っていうのも、三角形の内角の和が\(180^\circ\)ってことから
3つの角を知ることができるよね。なので、
三角形において「2組の角が等しい」➡︎「3組の角が等しい」➡︎「相似」って
ことが言えるってことなんだね。
この3つのが「三角形の相似条件」になるんだね。
この三角形の相似条件はよく使われるものになるので、しっかりと理解してして覚えておこう。
<三角形の相似条件>
①3組の辺の比がすべて等しい
②2組の辺の比が等く、その間の角が等しい
③2組の角がそれぞれ等しい
(4) 相似な三角形と相似条件
三角形の相似条件っていうのがわかったところで具体的に利用方法を見て行ってみよう。
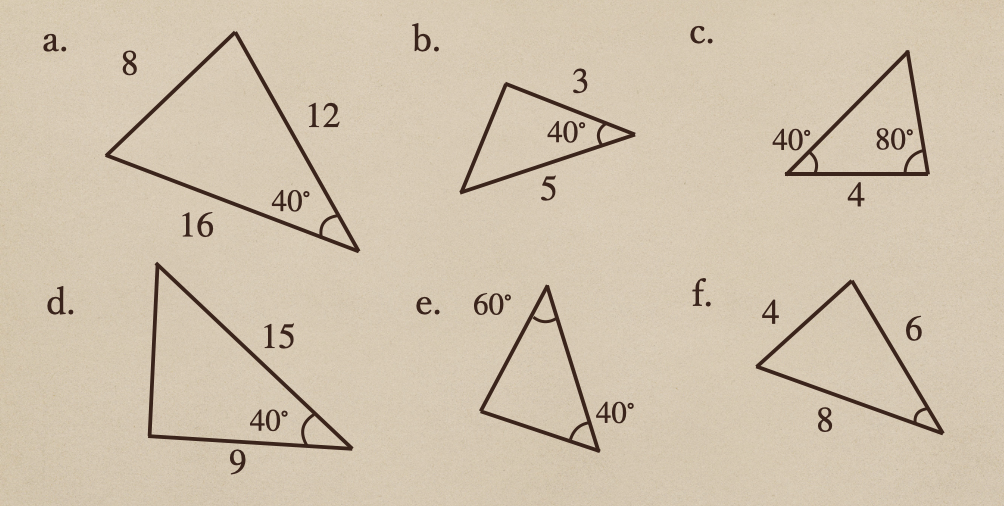
ここに6つの三角形があるんだけど、ここから相似な三角形を見つけてみよう。
その時の相似条件がなんなのかっていうのも確認してみよう。
ここで、確認するのは「三角形の相似条件」で
①3組の辺の比がすべて等しい
②2組の辺の比が等しく、その間の角が等しい
③2組の角がそれぞれ等しい
この3つの条件に当てはまる三角形をそれぞれ、選んであげればいいって事ですね。
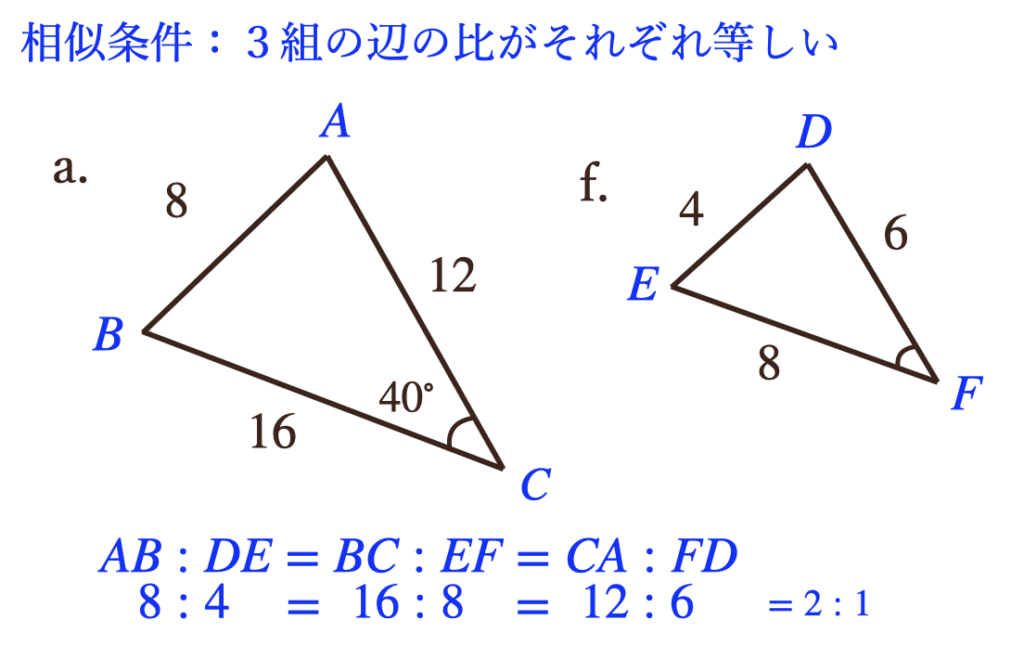
まずは、①3組の辺の比がすべて等しいを見ていくと、これは三角形の3組の辺が
わかっているので、6つの三角形から3組の辺がわかっているのは、\(a\)と\(f\)ってことで
あとは、これらの対応する辺どうしの比が等しいかっていうのを見てあげて
対応するのは\(a:f\)が\(8:4\)、\(12:6\)、\(16:8\)なので、どの辺も\(2:1\)に
なっているってことだね。なので、これは「3組の辺の比がそれぞれ等しい」って事なので
\(a\)と\(f\)は相似ですってことだね。
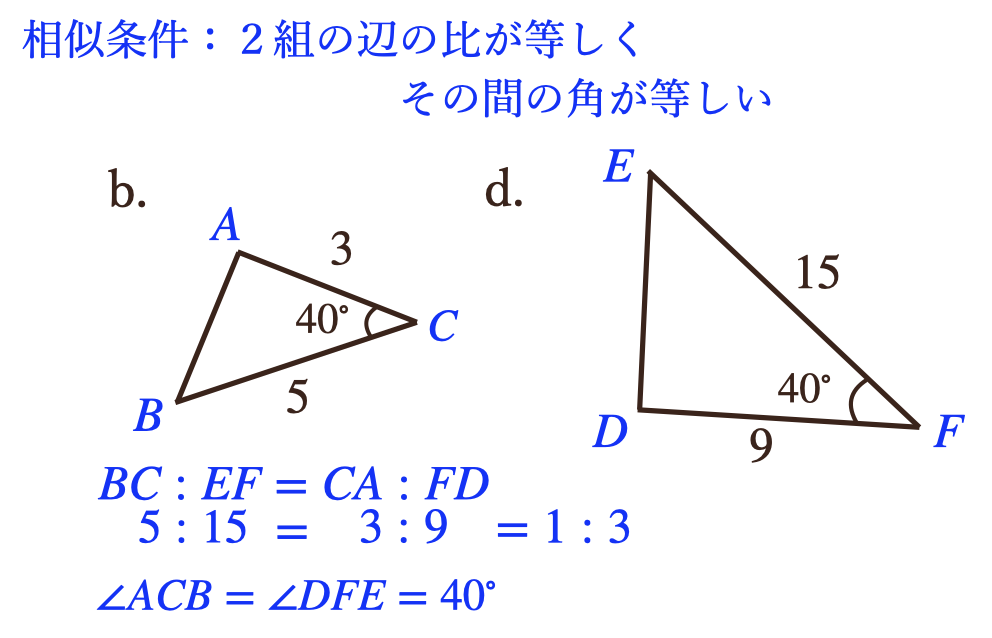
次に、②2組の辺の比が等しく、その間の角が等しいっていうのを考えてあげると
ここで、2組の辺がわかっていて、なおかつその間の角がわかっているのは
\(b\)と\(d\)となって、角の方は、どちらの三角形も\(40^\circ\)ってことで等しく
辺の比は\(b:d\)が\(3:9\)と\(5:15\)になっていて、どちらも\(1:3\)となっているので
2組の辺の比も等しいですよってことですね。なので、この\(b\)と\(d\)も相似ですってことが
言えるってことになるね。
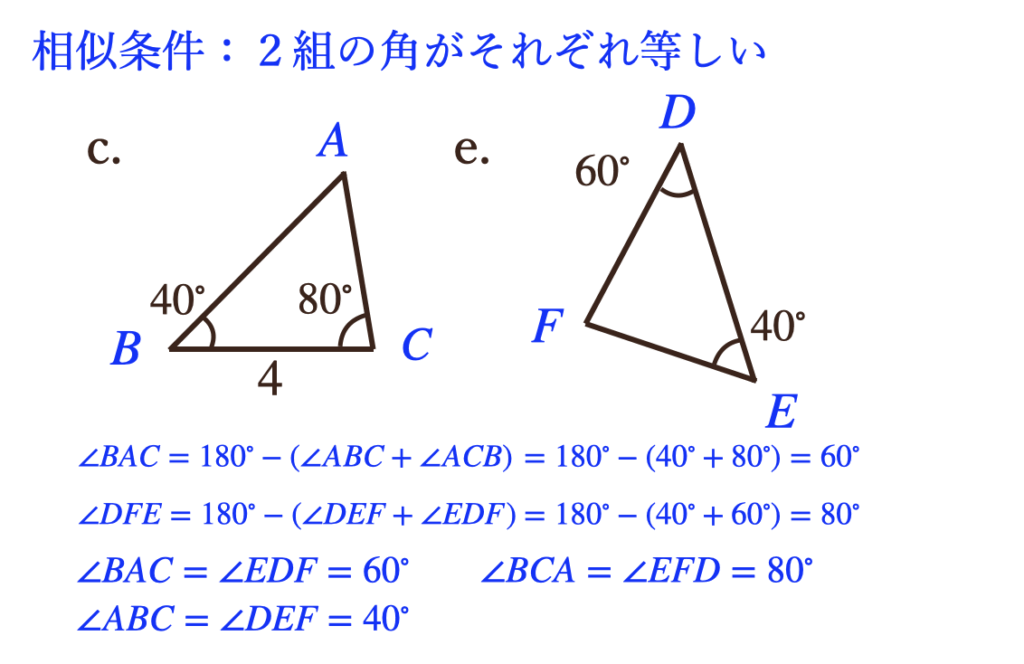
最後に③2組の角がそれぞれ等しいってことなんですけど、選ばれていない三角形の
\(c\)と\(e\)を見てあげると、\(c\)の方は、\(40^\circ\)と\(80^\circ\)で\(e\)の方は
\(40^\circ\)と\(60^\circ\)ってことで、一見、角が等しくないってなるんだけど
ここで、三角形の内角の和を考えたときに、わかっていない角っていうのが
\(c\)では、\(180^\circ-(40^\circ+80^\circ)=60^\circ\)となって
\(e\)では、\(180^\circ-(40^\circ+60^\circ)=80^\circ\)となっていて
これで、それぞれの三角形の内角は\(40^\circ\)と\(60^\circ\)と\(80^\circ\)って
ことになるんだね。
これで、「2組の角がそれぞれ等しい」ってことを満たしたことになるので
\(c\)と\(e\)は相似ですってことが言えたよね。
これらを整理してあげるとこう言うことだね。
これが、三角形の相似条件てことになりますね。
(5) 三角形の相似条件を使った証明
次の\(g\)、\(h\)、\(i\)の図形で相似な三角形を見ていくと。。
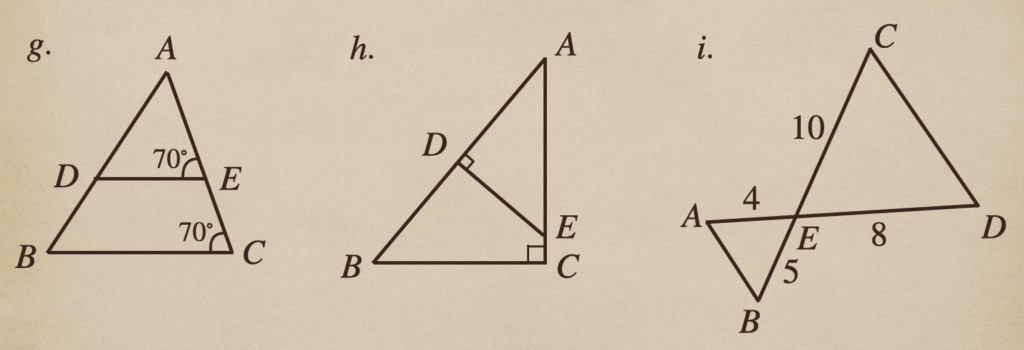
\(g\)の図では\(\triangle{ABC}\)と\(\triangle{ADE}\)が相似で
\(\angle{ACB}=\angle{AED}=70^\circ\)と\(\angle{BAC}=\angle{DAE}\)でこれは
共通な角だから等しいってことだね。
これで「2組の角がそれぞれ等しい」ので\(\triangle{ABC}\)∽\(\triangle{ADE}\)ってことですね。

次に\(h\)の図では、\(\triangle{ABC}\)と\(\triangle{AED}\)が相似ってことになるんだね。
さっきの\(g\)の相似とは対応する頂点が違ってくるので注意しないといけないね。
この三角形の相似条件を見ていくと\(\angle{BCA}=\angle{EDA}=90^\circ\)と\(\angle{BAC}=\angle{EAD}\)で
\(\angle{BAC}\)と\(\angle{EAD}\)は共通な角なので等しいってことですね
これでこれで「2組の角がそれぞれ等しい」ので\(\triangle{ABC}\)∽\(\triangle{AED}\)ってことですね。

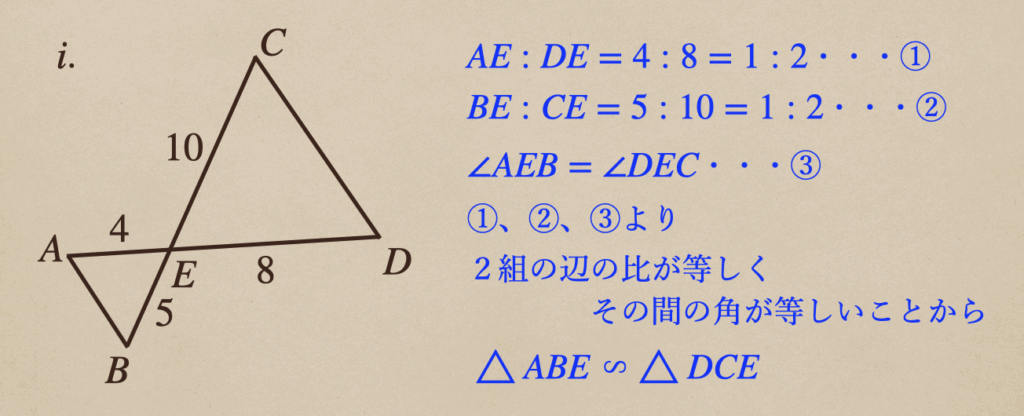
最後の\(i\)の図では、\(\triangle{ABE}\)と\(\triangle{DCE}\)が相似になってて
\(AE:DE=4:8=1:2\)で\(BE:CE=5:10=1:2\)ってことなので2組の辺の比が等しい
ってことですね。それと対頂角は等しいので、\(\angle{AEB}=\angle{DEC}\)って
ことで、「2組の辺の比が等しく、その間の角が等しい」ことから
相似ですよってことになりますね。
こんな風に、図形から相似条件に必要な情報を集めてきて
相似であるかどうかって言うのが証明できるんだね。
今回は、ここまでになります。
ここまでの記事が良かったと思ったらここをクリックしてね。
質問なんかがあった場合はコメントにお願いします。
では、また、さようなら。

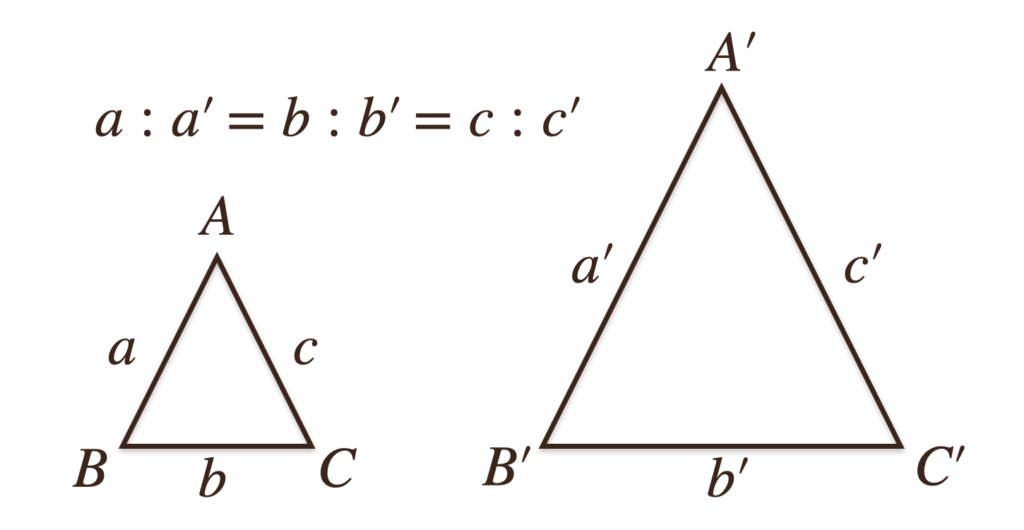
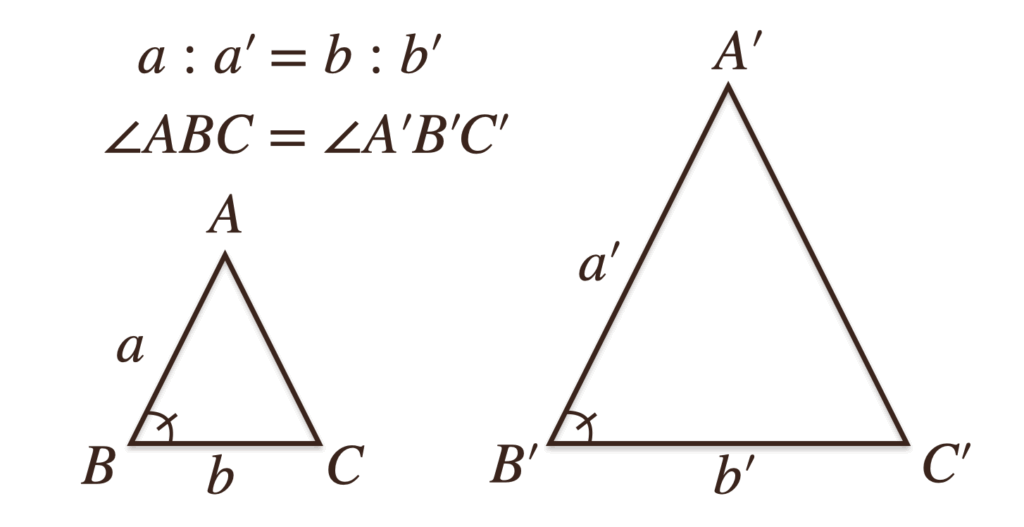
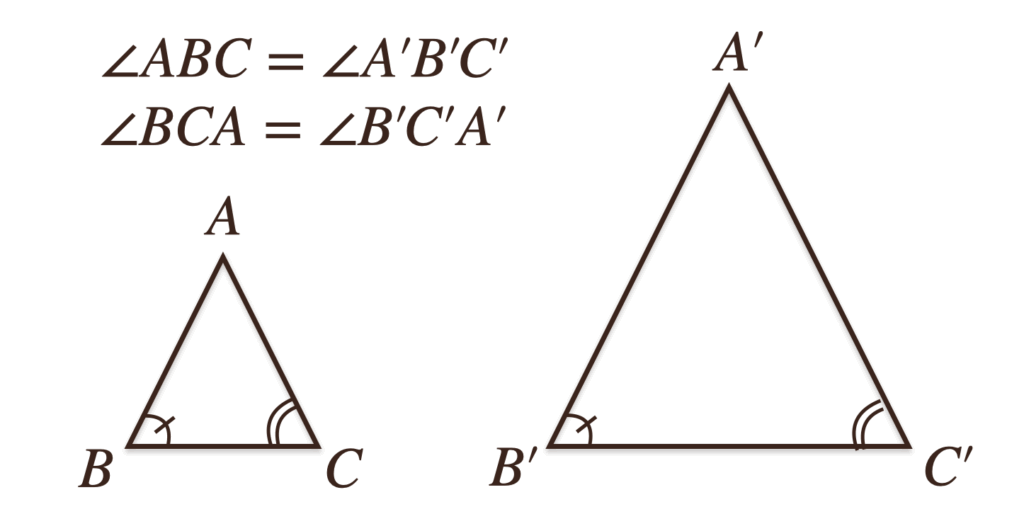
.jpeg)

コメント