どうも、こんにちはDKです。
中学2年生で習う、平行と合同の続きやっていきますね。
今回は、平行と合同の「図形の合同」についてやっていきましょう。
動画でも解説しているので、よかったらこっちも見てみてください。
(音が出るので注意して)
(1)合同な図形
まずはこの図を見てもらって。
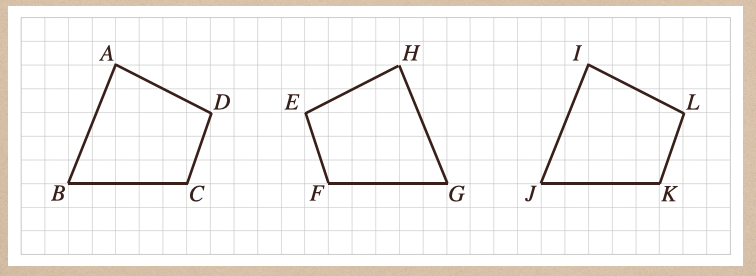
この3つの図形、四角形ABCD、四角形EFGH、四角形IJKLで
四角形ABCDと四角形IJKLっていうのは、同じ形をしていますよね。
そして、四角形EFGHは形が違うって思うかもしれないんだけど、これは
四角形ABCDを反転させている形になっているってことなんだね。
そして、この3つの四角形のように移動(反転、回転)させて重ね合わせることが
できる図形のことを合同(ごうどう)っていう言い方をするんですね。
この合同っていうのは、同じ形をしているものってことなので、こんな性質があるんだね。
【合同な図形の性質】
1.対応する線分の長さはそれぞれ等しい
2.対応する角の大きさはそれぞれ等しい
同じ形をしているんだから、当たり前って思うかもしれないんだけど
これが、性質ってことなるので、しっかり覚えておこうね。
この合同な図形を記号 ”\(\equiv\)” で表して
四角形ABCD \(\equiv\) 四角形EFGH
って表すことで、四角形ABCDと四角形EFGHは合同ですよって言ってるんだね。
今回の例は四角形で解説したんだけど、この合同っていうのは
他の多角形にも同じことが言えるんだね。
辺の数が等しい2つの多角形は
1.対応する辺の長さはそれぞれ等しい
2.対応する角の大きさはそれぞれ等しい
四角形の時と同じことをが言えるってことだね。
合同っていうのは、四角形EFGHのように反転していたり、回転(逆さ)向いている
図形でも、同じ形をしていれば合同ってことになるので、反転や回転している
図形っていうのは、見た目で違う図形って思ってしまうかもしれないんだけど
辺の長さや角の大きさが同じかどうかっていうので、見ていくようにしましょう。
(2)三角形の合同条件
今度は三角形の合同っていうのを見ていくんだけど
三角形の合同は次のどれかがわかっていれば、合同ですよってことが言えるんだ。
①3つの辺の長さが等しい
②2つの辺の長さとその間の角の大きさが等しい
③1つの辺の長さとその辺の両端の角の大きさが等しい
①の3つの辺の長さが等しい時っていうのは、三角形の形が決まってくるよね。
なので、3つの辺の長さがそれぞれ等しい2つの三角形は同じ形になる。。
すなわち、合同ですよってことになるんですね。

2つの辺の長さが等しくて、1つの辺の長さが違ってくると
三角形は作れたとしても、合同でないってことになるよね。
②の2つの辺の長さとその間の角の大きさが等しい場合っていうのは
その間っていうのがポイントで、2つの辺の間の角の大きさが決まると
辺は、決まった方向にひかれることになって、辺の長さもそれぞれ同じ長さなので
頂点の位置が決まって2つの三角形は合同になりますよってことなんですね。
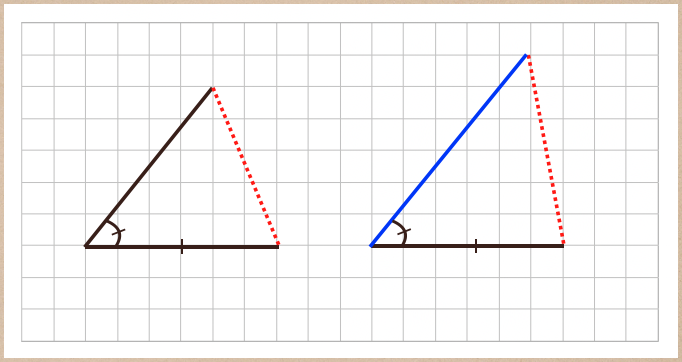
片方の辺の長さが違うと、三角形の形は同じものができないってことなので
合同ではないってことになるんですね。
角の大きさが違っても同じことが言えるってことですね。
③の1つの辺の長さとその辺の両端の角の大きさが等しいっていうのは、
これも、辺の長さが同じで、その両端から同じ角の大きさで線をひいて
交差する時っていうのは、同じ形の三角形になるってことなんだね。
こんな風に
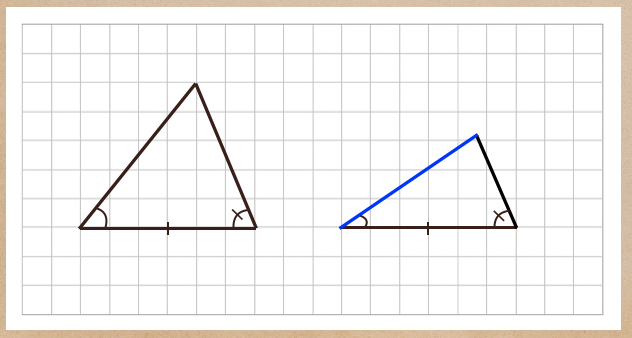
片方の角の大きさが違ってくるだけで、合同でない三角形になるんだね。
この三角形の合同条件っていうのは、ただ、覚えようとするのではなくて
辺や角のどこが同じであれば、同じ形の三角形になるのかっていうのを
考えられるようになると身についてくるよ。
ここで、三角形の合同条件のまとめやっておくね。
【三角形の合同条件】
1.3つの辺がそれぞれ等しい
2.2つの辺とその間の角がそれぞれ等しい
3.1つの辺とその両端の角がそれぞれ等しい
(3)合同な三角形と合同条件
今度は、この三角形の合同条件っていうのを使って、2つの三角形が合同かどうかっていうのを
判断していくっていうのを解説していきますね。
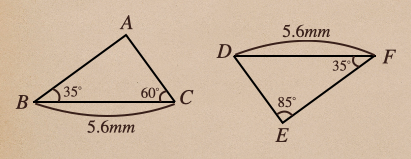
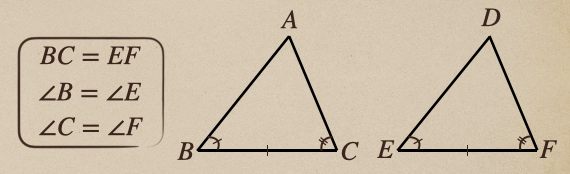
この三角形ABCと三角形DEFに関して、この2つの三角形が
合同かどうかを見ていきましょう。
まずは、辺の長さが書かれているところがあって、
BC=5.6mm 、DF=5.6mm なので、\(BC=DF\)ってことだね。
そして、\(\angle B\)=35° で \(\angle F\)=35° なので、\(\angle B=\angle F\)となるね。
じゃあ、\(\angle C\)=60° で \(\angle E\)=85° で、 \(\angle C≠\angle E\) となるので
この2つの三角形は「合同ではない」ってなるかっていうと。。
そうじゃくて、三角形で2つの頂点の角がわかっているってことなので
残りの頂点の角っていうのもわかるよね。
\(\angle A\)=180°-(60°-35°)=85° で計算できて
\(\angle D\)=180°-(85°-35°)=60° で計算できて
\(\angle A\)=85° で \(\angle E\)=85° なので、\(\angle A=\angle E\)
\(\angle C\)=60° で \(\angle D\)=60° なので、\(\angle C=\angle D\)
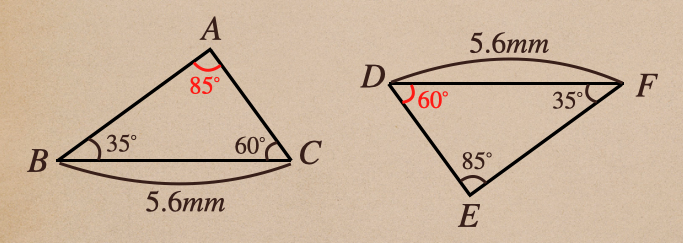
これだけの辺と角の値がわかったよね。ここから三角形の合同条件っていうのが
3つあったと思うんだけど、どれに当てはまるかっていうのを考えてあげると
【三角形の合同条件】
1.3つの辺がそれぞれ等しい
2.2つの辺とその間の角がそれぞれ等しい
3.1つの辺とその両端の角がそれぞれ等しい
\(BC=DF\)・・・①
\(\angle B=\angle F\)・・・②
\(\angle C=\angle D\)・・・③
①、②、③から「1つの辺とその両端の角がそれぞれ等しい」ってことが言えて
この\(\bigtriangleup ABC \equiv \bigtriangleup EFD\)であるってことが
言えるってことになるんだね。
ここで、三角形のABCと三角形DEFを合同を表した式で書いた時
\(\bigtriangleup ABC \equiv \bigtriangleup EFD\)って書いたよね。
ここで、\(\bigtriangleup ABC \equiv \bigtriangleup DEF\) と書いていないよね
これっていうのにも、意味があって、合同であることを説明するときには、
対となる頂点どうしを合わせて表してあげる必要があって、
今回でいいうと、頂点Aと頂点E、頂点Bと頂点E、頂点Cと頂点Fが対に
なっているので、\(\bigtriangleup ABC \equiv \bigtriangleup EFD\)と書いてあげる
必要があるってことなんだね。
(4)三角形の合同条件の使い方
2つの三角形が合同であるかどうかを説明できる方法がわかったところで
今度は、こんな問題があった場合を考えてみよう。
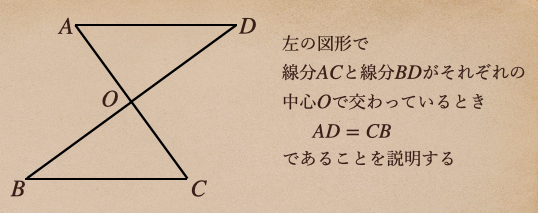
こういった、問題では、三角形AOBと三角形BOCが合同であるってことを
言えれば、AD=CBってことが言えるってことになるんだね。
あとは、出題されているところからわかっていることを見ていって
三角形の合同条件を説明できればいいってことになるんだね。
まずは、「線分ACと線分BDの中心に点Oがある」ってことなので
線分AOと線分COは等しいってことだよね。
また、線分BOと線分DOも同じく等しいってことになるよね。
なので、AO =CO、BO=DOってことが言えるってことなんだね。
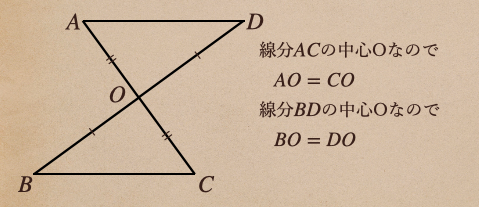
これで2つの辺がそれぞれ、等しいってことが言えたよね。
あとは、三角形の合同条件から、「3辺が等しい」もしくは、「2つの辺と、その間の角が等しい」って
ことが言えれば、いいってことだね。
ここで「3辺が等しい」っていうのは、出題でも聞かれているAD=CBの部分になっていて
これを今、説明しようとしているので、わかっていないことで、今ある情報からでは
それを説明することはできないよね。
残るは「2つの辺と、その間の角が等しい」ってことなので、
\(\angle AOD\)と\(\angle COB\)が等しいことが言えればいいってことになるね。
ここで、この図形から\(\angle AOD\)と\(\angle COB\)は対頂角になっているよね
そして、対頂角の性質で、「対頂角は等しい」っていうのがあったよね。
ってことで、この\(\angle AOD\)と\(\angle COB\)が等しいってことが言えたってことだね。
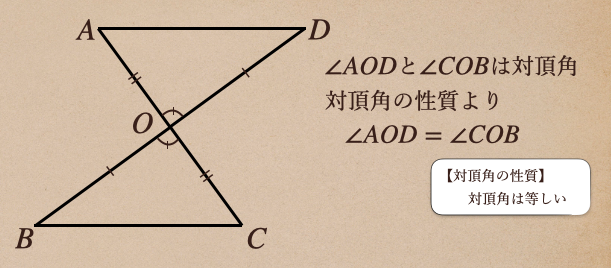
これで、三角形の合同条件である「2つの辺と、その間の角が等しい」ことが
言えたことになるね。なので、\(\bigtriangleup AOD \equiv \bigtriangleup COB\)ってことが
言えたよね。2つの三角形が合同ってことなので\(AD=CB\)ってことが言えるってことなんだね。
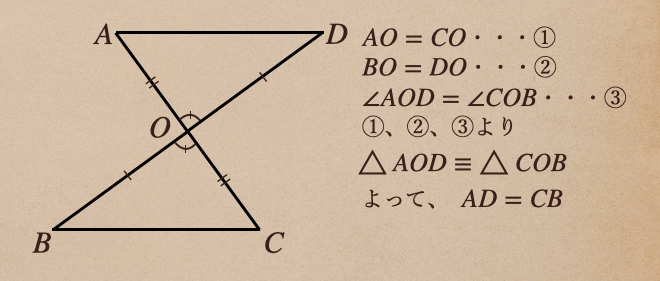
こんな風に、わかっていることがらを根拠として、あることがらが成り立つことを説明することを
証明っていう言い方をするんだね。
この証明する問題っていうのは、今までに習ってきた数学の定義や性質っていうのを
根拠に、あることがらって言うのが成り立っていることを説明していく必要があるんだね。
なので、数学の定義、性質っていうのを忘れてしまっているとこの証明のところで
つまづいてしまうことにもなるので、改めて、基礎の見直しっていうのを行なっておいてくださいね。
今回は、ここまでになります。
ここまでの記事が良かったと思ったらここをクリックしてね。
質問なんかがあった場合はコメントにお願いします。
では、またさようなら






コメント