どうも、こんにちはDKです。
今回は中学3年生で習う円についてやって行きますね。
円て言うのは言葉の通り「マル」の図形になるんだけど、すでに習った中心角と
ここで学ぶ円周角(えんしゅうかく)って言うものの関係やそれの定理って
言うのがあって、これを学ぶことで図形に関してさらにいろいろなことが
見えてくるようになるんだね。
この円についての基礎的なものは中学1年生で習っているんだけど
ここでの円を学ぶこと前に基礎をもう一度おさらいしたいって人は
「中1-5.平面図形(3)」を見てみてください。
円とは?から中心角、弧についての解説を行なっていますよ。
それでは、こっちの「円」についてやって行きますね。
[1]円周角の定理
ここでは、円周角の定理を解説していくんだけど
まずは、「円周角(えんしゅうかく)」が何なのかって言うのを見て行こう。
円周角っていうのは言葉にして書くと。。
円\(O\)の\(\stackrel{\frown}{AB}\)の両端\(A\)、\(B\)と\(\stackrel{\frown}{AB}\)を
除いた円周上の点\(P\)を結んでできる\(\angle{APB}\)を\(\stackrel{\frown}{AB}\)に対する
円周角と言う。\(\stackrel{\frown}{AB}\)を\(\angle{APB}\)に対する弧と言う。
ってことなんだね。これを図で言うと。。。
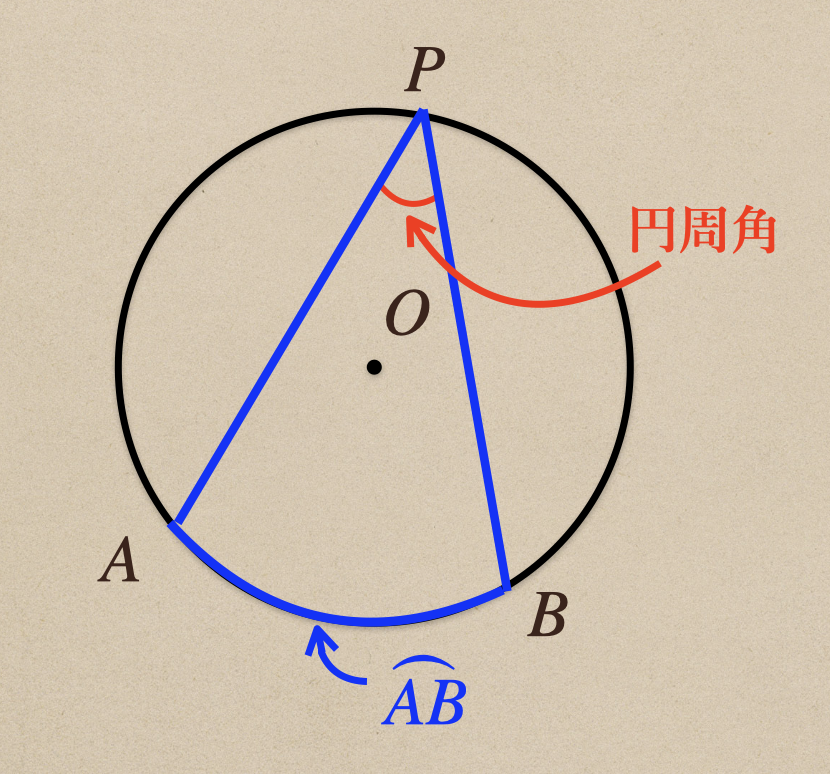
ってことになって、\(\stackrel{\frown}{AB}\)の中心角って言うのは1つしかないんだけど
円周角っていうのは、いろいろな位置にかくことができるものになるんだ。
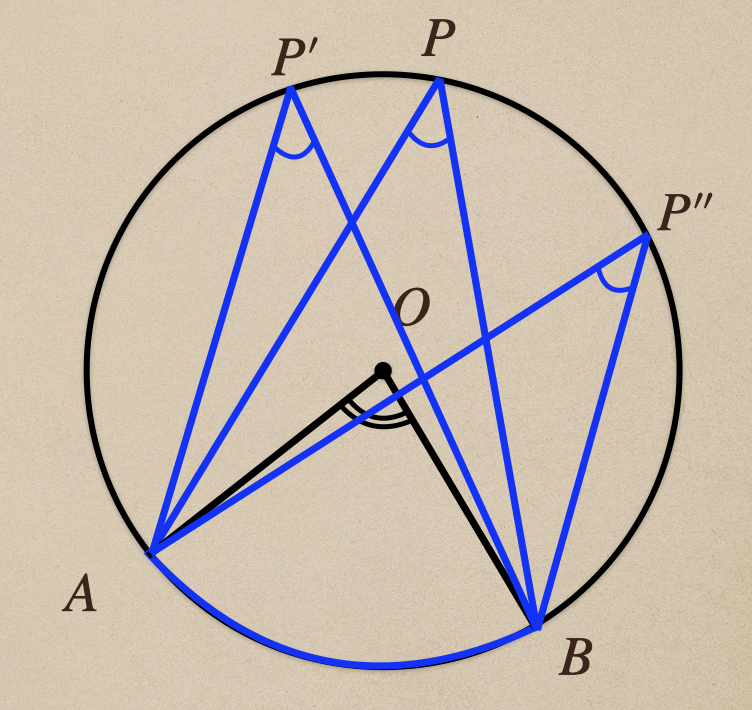
この時に、いろいろな位置にかかれた円周角は点\(P\)が\(\stackrel{\frown}{AB}\)上をのぞいた
円周上を動く場合、次の3つの位置関係にあることが言えるんだね。
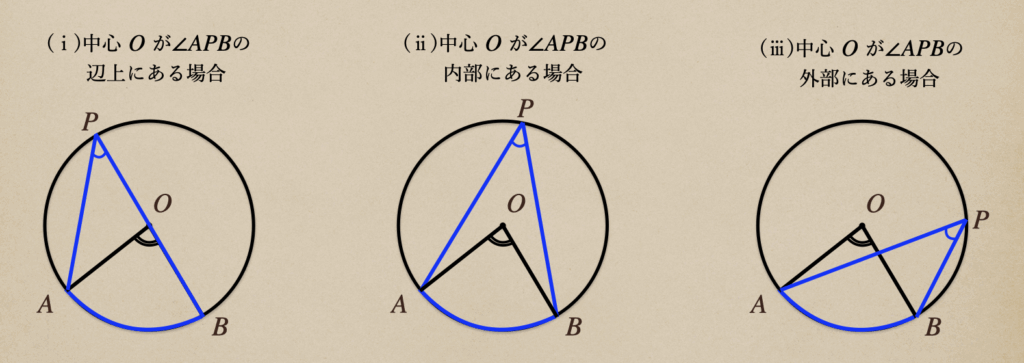
この3つの位置関係にある円周角\(\angle{APB}\)の大きさが中心角\(\angle{AOB}\)の
大きさの半分であることが証明できれば、同じ弧の中心角と中心角はどこをとっても
同じ関係にあるってことが言えるんだね。
(ⅰ)中心\(O\)が\(\angle{APB}\)の辺上にある場合
これは、\(\triangle{AOP}\)がどんな三角形なのかっていうのを考えてあげれば
そこから、中心角\(\angle{AOB}\)と円周角\(\angle{APO}\)の関係が見えてくるんだね。

これで、中心角\(\angle{AOB}\)が円周角\(\angle{APO}\)の半分であることが
証明されたってことになりますね。次に
(ⅱ)中心\(O\)が\(\angle{APB}\)の内部にある場合
ここでは、点\(P\)と\(O\)を直線で結んであげて、反対の円周上との交点を\(C\)と
してあげて、\(\triangle{AOP}\)と\(\triangle{BOP}\)で考えてあげるんだね。
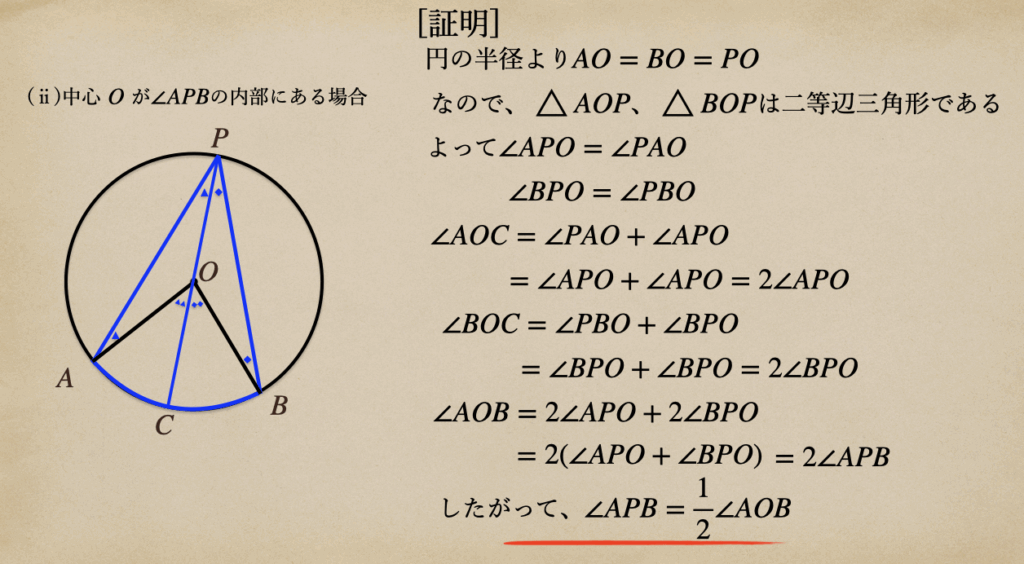
ここでも、中心角\(\angle{AOB}\)が円周角\(\angle{APB}\)の半分であることが
証明されたってことになりますね。最後に
(ⅲ)中心\(O\)が\(\angle{APB}\)の外部にある場合
これも、(ⅱ)で引いてあげたようにここでは、点\(P\)と\(O\)を直線で結んであげて
反対の円周上との交点を\(C\)としてあげて考えていくんですね。
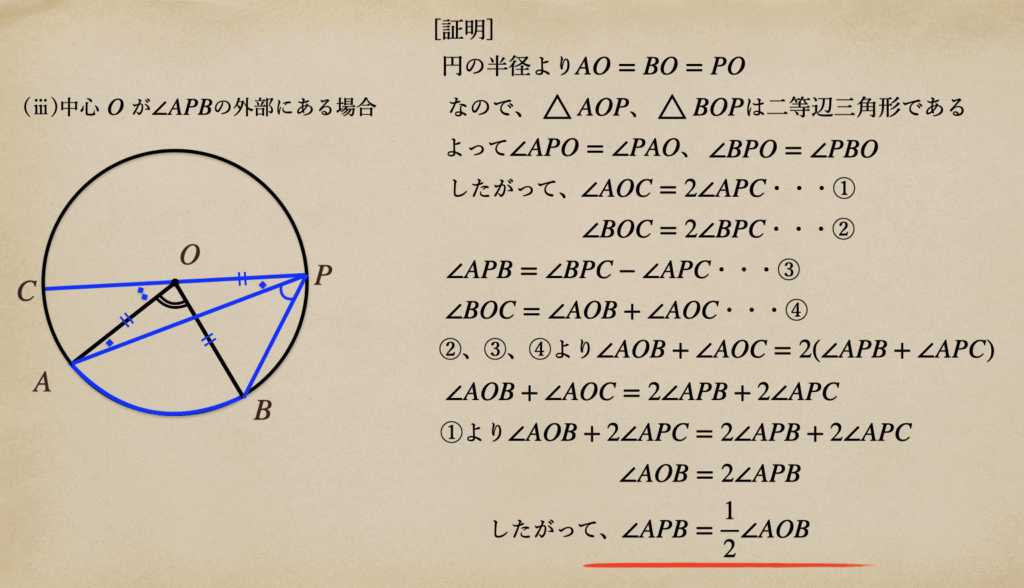
ここでも、中心角\(\angle{AOB}\)が円周角\(\angle{APB}\)の半分であることが
証明されたってことになりますね。
この(ⅰ)〜(ⅲ)が証明されたことで、中心角に対して円周角っていうのはどこをとっても
中心角の半分になるって、これを【円周角の定理】っていうんだね。

これは、「円」の中でもよく使われていくものになるので、しっかり理解して覚えておこう。
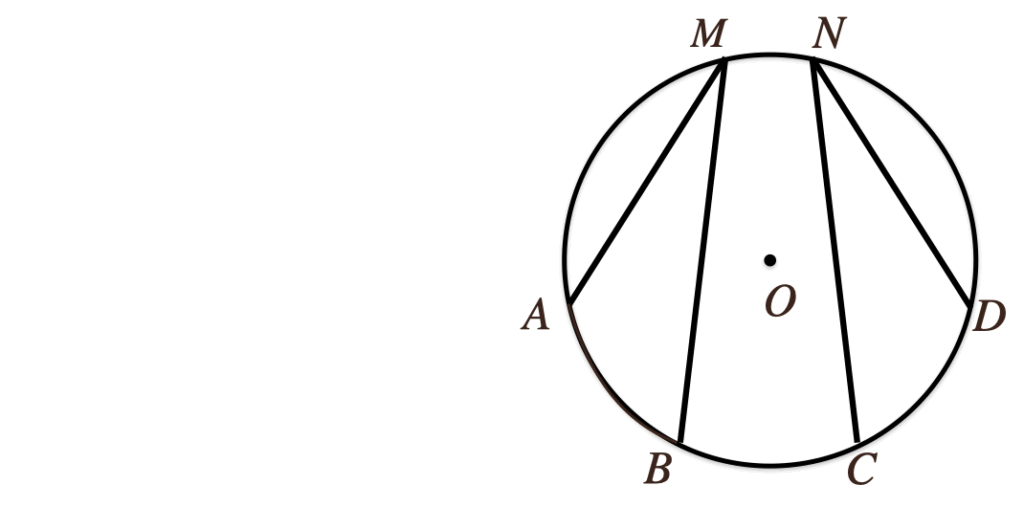
[2] 弧と円周角
次は、弧と円周角の関係について見て行きますね。
この弧と円周角の関係を見ていく前に、まずは、弧と中心角の関係っていうのがあったよね。

この「弧と中心角」について成り立っていることが弧と円周角の関係でも
同じことが言えるのかどうかっていうのを証明を使って確認していってみよう。
(ⅰ)\(\angle{AMB}=\angle{CND}\)ならば\(\stackrel{\frown}{AB}=\stackrel{\frown}{CD}\)であることを証明する
これを証明していくには、まずそれぞれの中心角が等しいことが証明できれば
中心角が等しければそれらの弧は等しくなることが言えるってことなので。。。
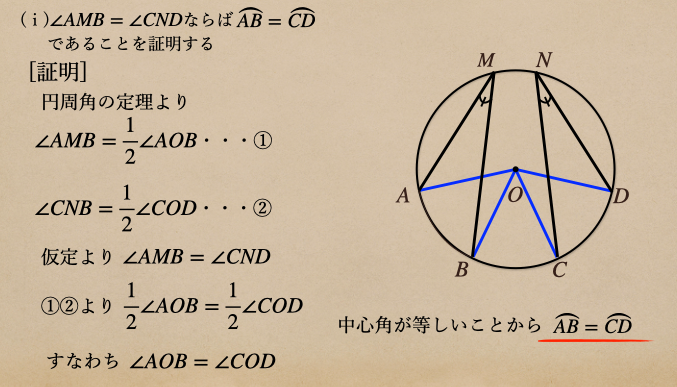
これで、円周角が等しければ弧が等しいことが言えることが証明されたってことですね。
次に、(ⅰ)の逆のことを証明していこう。
(ⅱ)\(\stackrel{\frown}{AB}=\stackrel{\frown}{CD}\)ならば\(\angle{AMB}=\angle{CND}\)であることを証明する

ここでも、弧が等しければ中心角も等しいことを利用して、あげて証明していって
あげればいいってことだね。
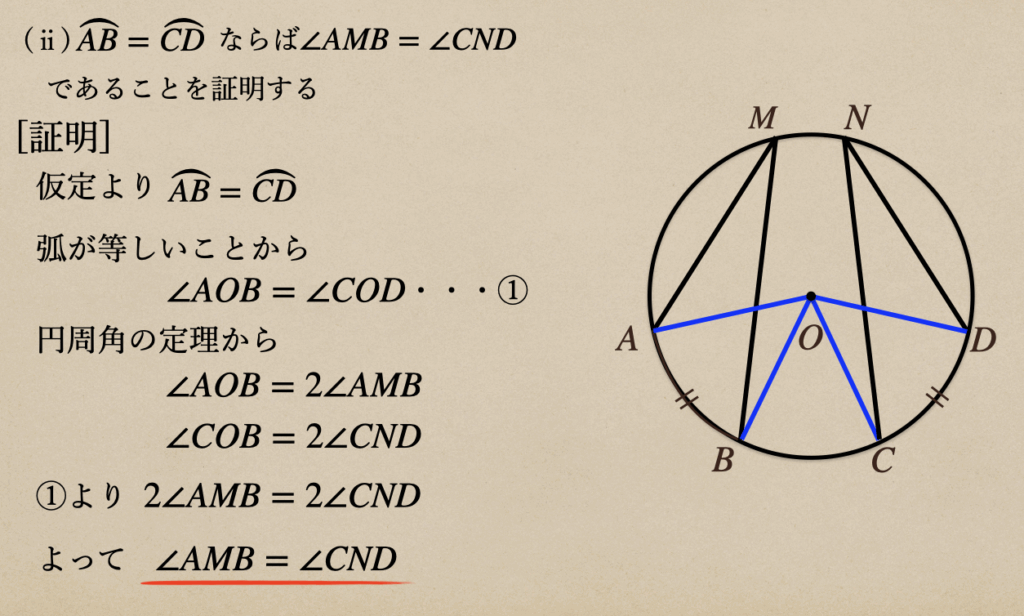
これで、弧が等しいと円周角も等しいってことが言えたので「弧と円周角」の定理として

また、1つの円で中心角の大きさと弧の長さは比例することから
円周角の定理から次のことも言えるってことになるんだね。
1.円周角の大きさは、それに対する弧の長さに比例する
2.弧の長さは、それに対する円周角の大きさに比例する
ここも、重要なポイントになってくるので、しっかり理解しておいてね。
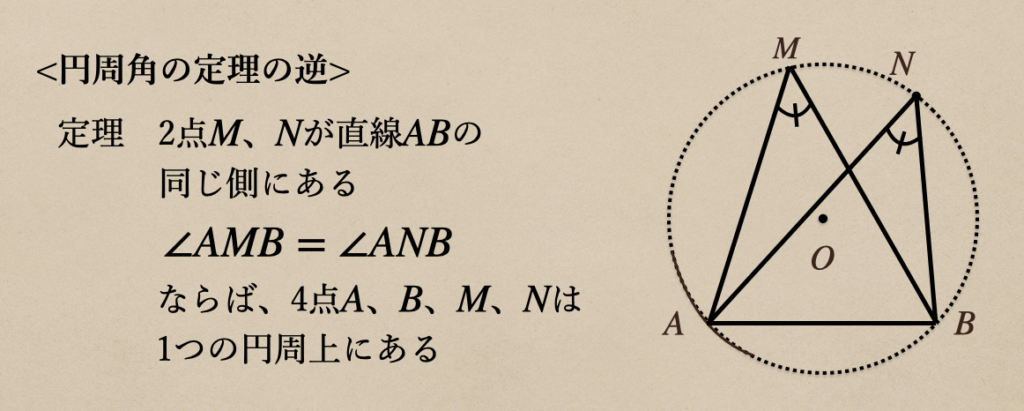
[3] 円周角の定理の逆
円周角の定理の逆っていうのは、円周角の定理を逆に考えた時に同じことが
言えるのかっていうことなんだね。今までに習った単元でも同じような
「逆」の定理っていうのがあったと思うんだけど、円においては、それが言えることで
さらにこんなことも言えますよってことがこの円周角の定理の逆の定理とされているんだね。
それを説明する前に、次のことを考えてみて。

円周上にある点\(A\)と\(B\)から、円の内側、円周上、円の外におかれた点\(N\)で
円周角\(angle{AMB}\)と\(angle{ANB}\)の大きさの関係っていうのを
考えていくってことだね。
ここで、考えるのはそれぞれ\(\angle{AN_{1}B}\)と\(\angle{AN_{2}B}\)の関係と
\(\angle{AN_{2}B}\)と\(\angle{AN_{3}B}\)の関係っていうのを考えてみると
わかってくるんだね。
まずは、\(\angle{AN_{1}B}\)と\(\angle{AN_{2}B}\)の関係を見ていくと
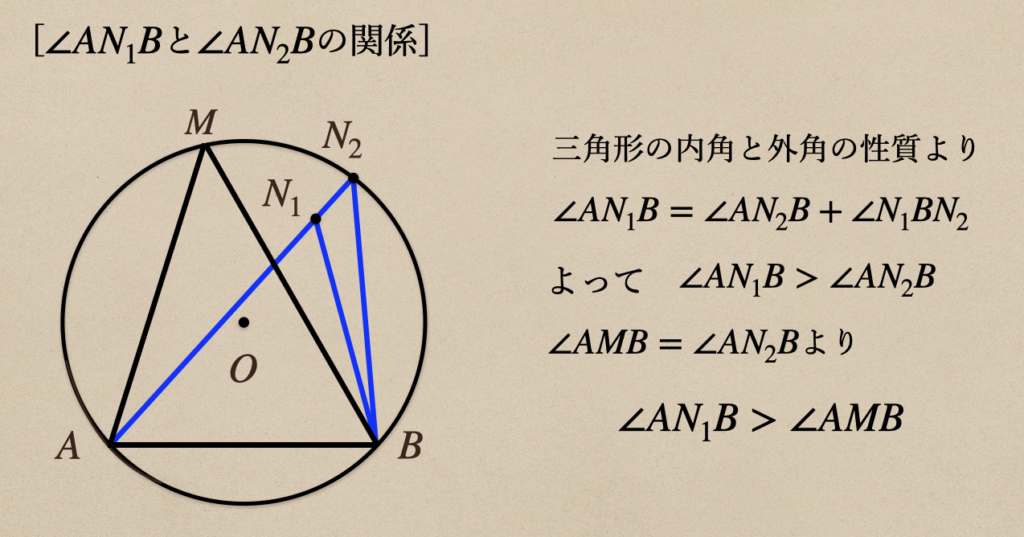
点\(N_1\)の場合だと、円周角より角度が大きくなるってことになるんだね。
次に、\(\angle{AN_{2}B}\)と\(\angle{AN_{3}B}\)の関係を見てみると
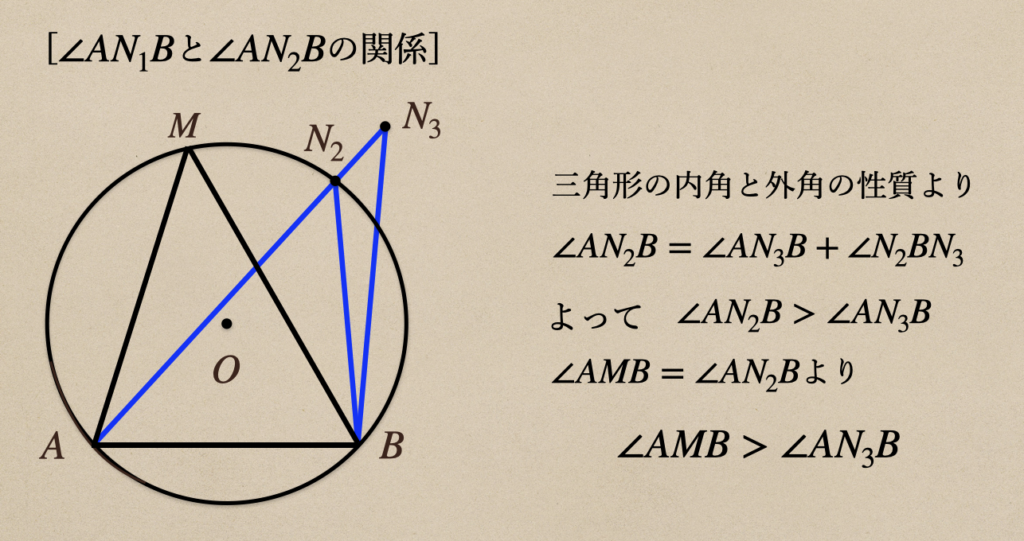
今度は点\(N_3\)の場合だと、円周角より角度が小さくなることがわかるよね。
これらから、点\(N_1\)、\(N_2\)、\(N_3\)の位置と円周角である\(\angle{AMB}\)の
関係っていうのはこんな風になっているんだね。
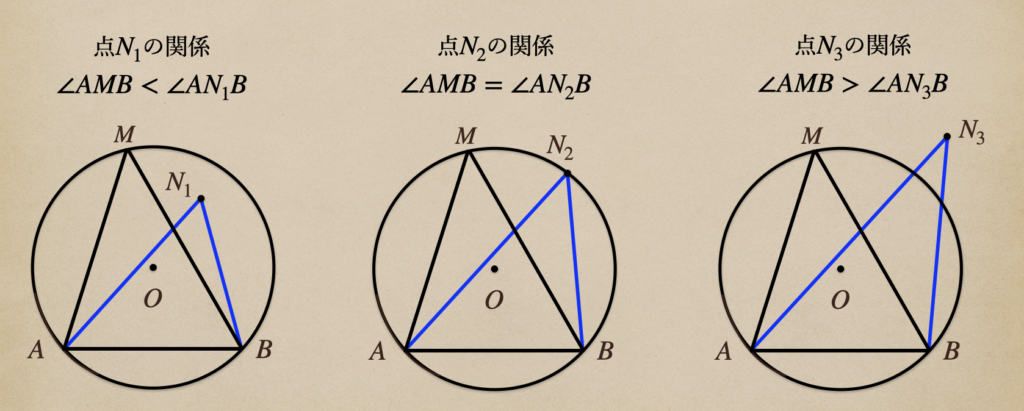
円に対して点が円の内側にあると円周角より大きくて、円の外側にあると円周角より
小さくなっていて、円周上を境に円周角との大きさが変化していることがわかるよね。
このことから円周角の定理の逆として定理が言えるんだね。
ちなみに、\(\angle{AMB}=\angle{AQB}=90^\circ\)のときっていうのは
\(AB\)っていうのは、円の直径とする円周上にあるってことになるんだね。
[4] 円の性質の利用
ここまでに、円の性質っていうのを学んできたので、この円の性質を利用して
次のことをやってみよう。
[1] 円の中心を求める
円の中心の求め方っていうのは色々あるんだけど今回は、三角定規を使って
中心を求めてみよう。ここまでに習った円の性質の中で、中心角と円周角の関係から
求めていくことができるんだね。
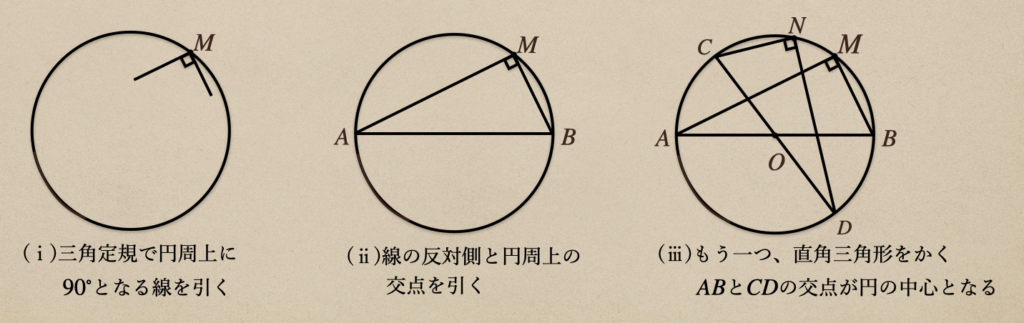
円周角の定理で「円周角は中心角の半分」っていうのがあったよね。
これを利用して、直径っていうのは円の半分のおうぎ形ってことになるので
その時の中心角っていうのは\(180^\circ\)ってことだよね。
その中心角\(180^\circ\)の半分が円周角ってことなので、\(90^\circ\)ってことに
なるんだね。なので、円に直角三角形を2つ作ってあげれば、直径が2つできて
その交点が中心になるってことなんだね。
[2] 円の外にある点から接線を作図する
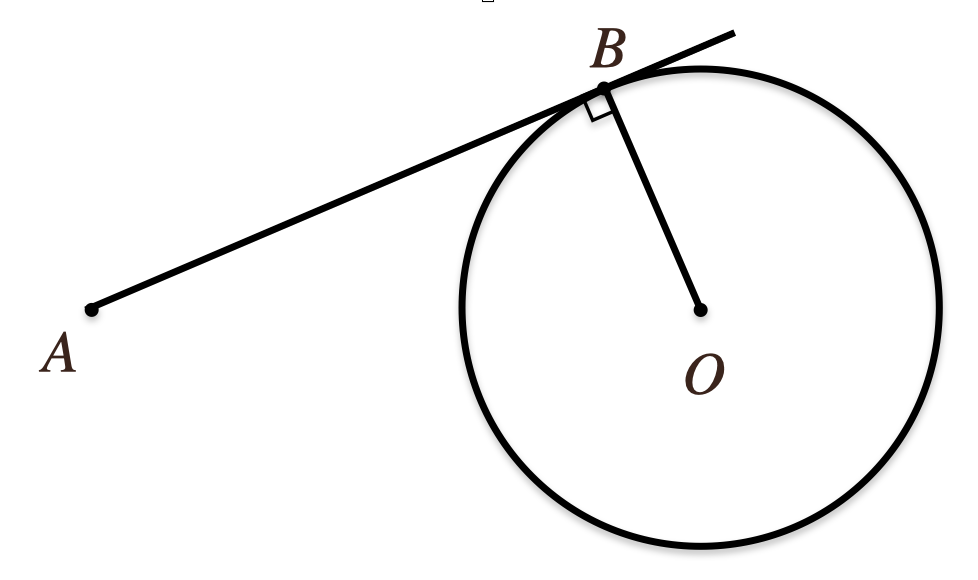
円の接線にも性質があって、点\(A\)から円\(O\)に接線がひかれてその接点を\(B\)と
すると接線\(AB\)と\(OB\)っていうのは\(90^\circ\)ですっていうのがあったよね。
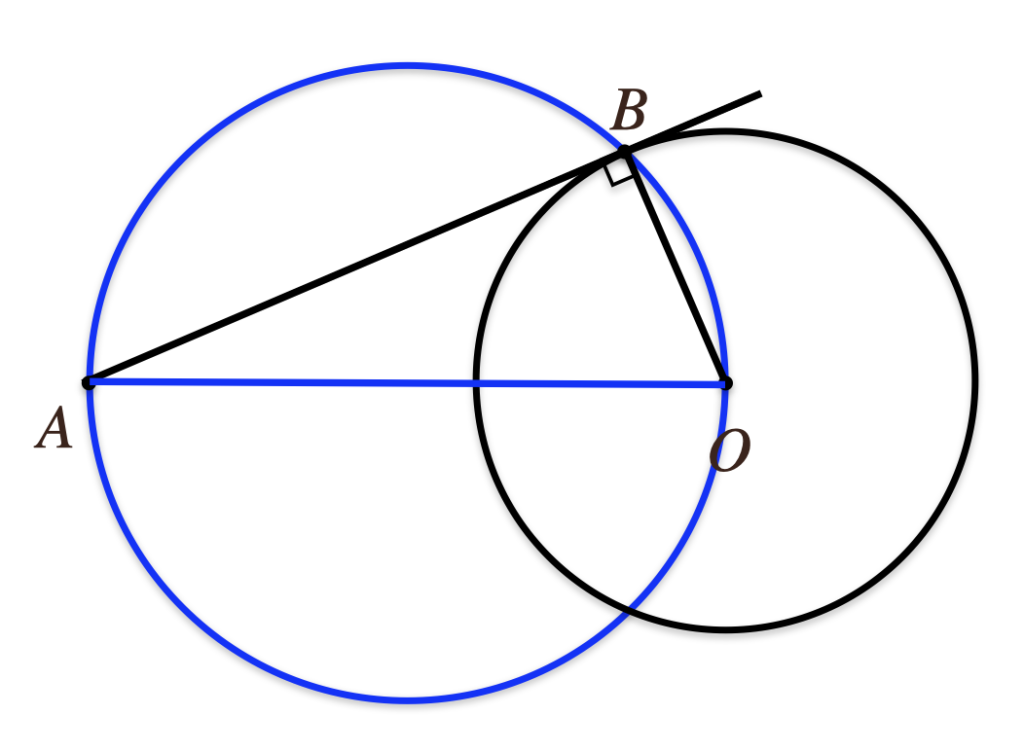
このことから、点\(A\)と\(O\)を通る円をかいてあげて、その円周上の点と
\(A\)と\(O\)を線で結んであげるとその角は\(90^\circ\)になるってことだよね。
ようするに、点\(A\)と\(O\)を通る円と円\(O\)の交点も点\(A\)と\(O\)を通る円の
円周上になるので、\(90^\circ\)になるってことだよね。
ここまで、理解できたらあとは、作図を行なっていけばいいってことなので
手順としては。。
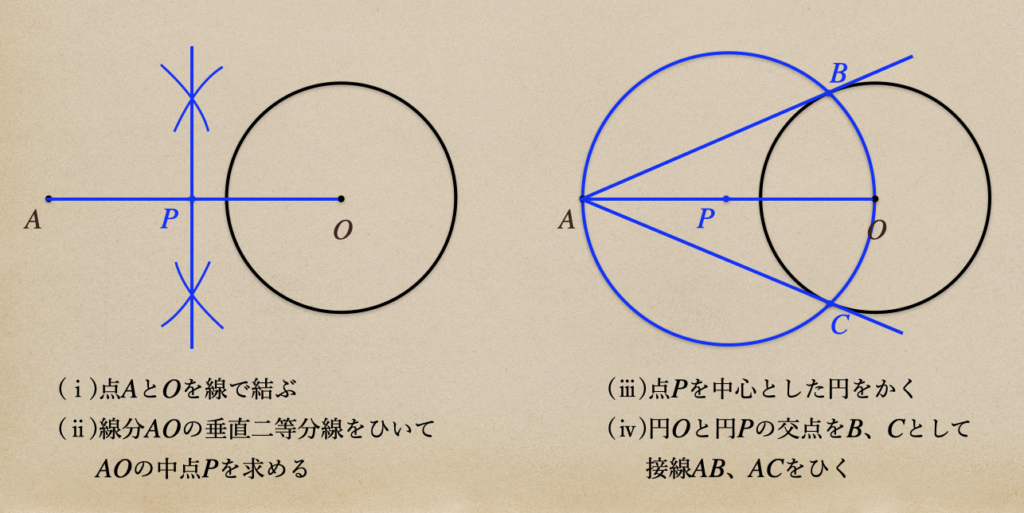
これで接線を作図することができたね。この作図での注意は接線は2つひくことが
できるってことだね。
次は作図ではないんだけど、円の性質を利用した証明になりますね。
[3] 円と2つの線分の関係
ここでは、円の中にある2つの線分をつなぎ合わせた時に三角形ができるんだけど
それらがどういった関係にあるのかっていうのを見ていこう。
ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー
円の内部に点\(P\)をおき、点\(P\)を通る2本の直線をひいて
円との交点を\(A\)、\(B\)、\(C\)、\(D\)とする
点\(A\)と\(C\)、\(B\)と\(D\)を結んでできる\(\triangle{APC}\)と\(\triangle{DPB}\)は
相似であることを証明する
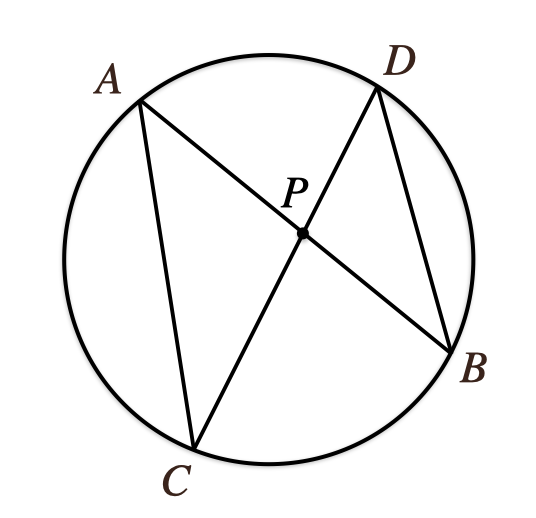
ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー
まずはこれを証明してみよう。

このことから、円周上におかれた4点で作られた三角形っていうのは
共通する弧があることから、角度が同じであることが言えて相似な関係に
あるってことになるんだね。
今回は、ここまでになります。
ここまでの記事が良かったと思ったらここをクリックしてね。
質問なんかがあった場合はコメントにお願いします。
では、また、さようなら。



コメント