どうも、こんにちはDKです。
今回は中学1年生で習う平面図形の3回目として、円とおうぎに関してやっていくよ。
平面図形には多角形、円の2種類の図形がよく使われるんだけど、
多角形にはない、円の特徴っていうのがいくつもあって、この多角形と円を組み合わせた
問題っていうのが本当によく出てくるんだね。
だから、平面図形としてこの円とおうぎに関してもしっかりと基礎を理解しておいてくださいね。
動画でも平面図形の基礎を公開しているのでこちらも見てみてください。
※音が出るので、周りに気をつけて再生してみてね。
では、早速、1つ目からやっていきますね。
円の性質
1つ目は円の性質についてやっていくね。
この円の性質っていうのは、この円とおうぎを学んでいく中でも基本となるところで
小学校でも、ある程度は習っていると思うので、おさらいのつもりで見てみてね。
まずは、円について
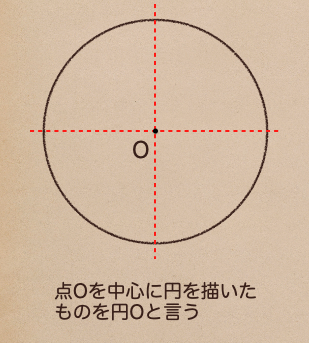
上の図のように点Oを中心に円をかいた場合、それを円Oって言う言い方で円を表すんだね。
ここで使われる中心点Oって言うのは、今後もよく使われて、一般的に円の中心はOで表すことが
多くなるので、覚えておこうね。2つの円を表したりする場合はそれぞれ中心点がちがってくくるので
『円Oと円Pの2つの円』って表される場合は点Oを中心とした円と、点Pを中心とした円の
2つがあるってことになるんだね。
必ずしも、中心点Oで表されるわけではないので
問題の内容に書かれた「どこを中心として書かれた円か」をしっかり確認しておこう。
次が円の性質となるところになるんだけど。。
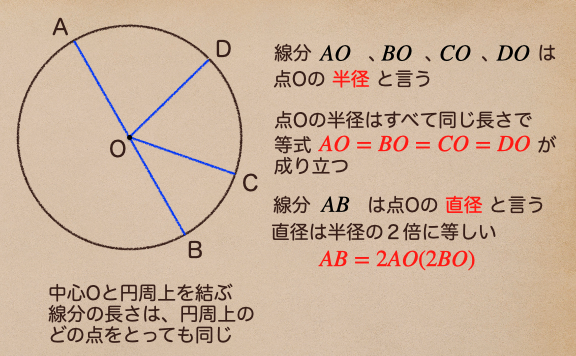
円Oの円周上に置かれた点A,B,C,Dと中心Oとを結んだ線分って言うのは
全て円Oの半径になるってことだね。だから、その線分はすべて等しくなるってことだね。
また、半径は円の半分の線分を指していて、直線は円の全長ってことになるから
直径AB=半径AO(BO)×2 ってことになるんだ。
こんなの当たり前って思うかもしれないけど、これを線分AOやABを使って式で表したり
今後の、図形問題ではこの半径、直径っていうところがポイントになることが多くなるから
しっかり、理解して覚えておこう。
次は円の円周上の中心ではないところに置かれた点を結んだ線についてだよ。
円の弧と弦
円の弧と弦について説明するね。
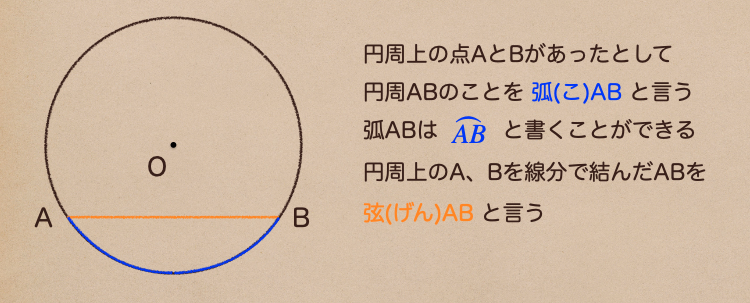
円周上の点同士を結んだ線を弧(こ)って言う言い方をするんだね、弧って言うのは
\(\stackrel{\frown}{AB}\) と書くことができて読み方は同じで「こAB」って言うんだね。
上のように線分ABを弦って言って弓の糸の部分と同じで「げん」って読むんだね。
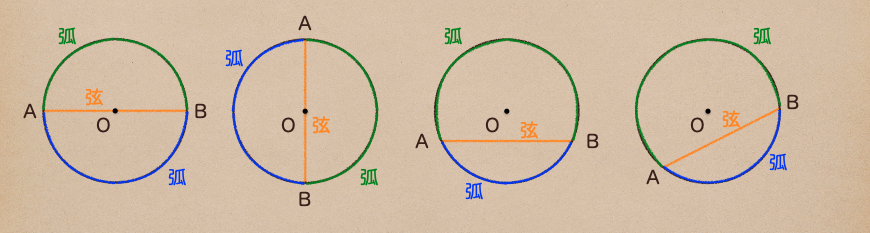
上の図のように弧って言うのは完成された円以外の円周上の線のことを指していて
青線、緑線それぞれ、弧ABと言うことができるんだね。
弦に関しても、線分が円周上の2点を通っていることが条件になるから
中心Oを通る線分、要するに直径も弦って言うことができるってことなんだね。
次はこんな場合の図形について説明するね。
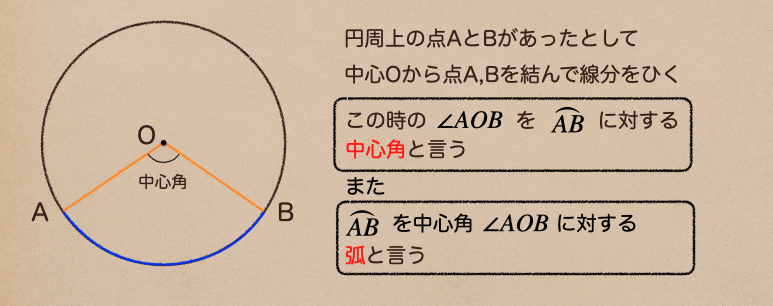
こんな風に中心Oから円周上に引かれた線分を
その対応する弧に対する \(\angle\mathrm{AOB}\) を中心角って言うんだ。
また、中心角 \(\angle\mathrm{AOB}\) に対応する弧って言う言い方をするんだね。
ようするに、その弧に対する中心角って言うのは1つしか存在しないってことになるから
どの弧と中心角がセットになっているのかって言うのも、注意して確認いこう。
円と直線
円と直線についてやっていくよ。
この円と直線っていうのは説明自体はシンプルになっているんだけど
問題を解く上でも大事になるところになるんだね
直線も囲ってしまえば三角形や四角形になるってことだから円と多角形の組み合わせを
理解したいなら、ここの円と直線をしっかり理解しておく必要があるんだね。

円に直線を引くってなると、上の図のようにいろいろな場所に引くことができるんだね、
その直線っていうのは、普通は円周との交点が2ヶ所できるんだ。
けれど、直線を円の外側でひくと円周との交点が1ヶ所だけになるところが存在するんだね。
そして、交点が1ヶ所だけとなる直線は…
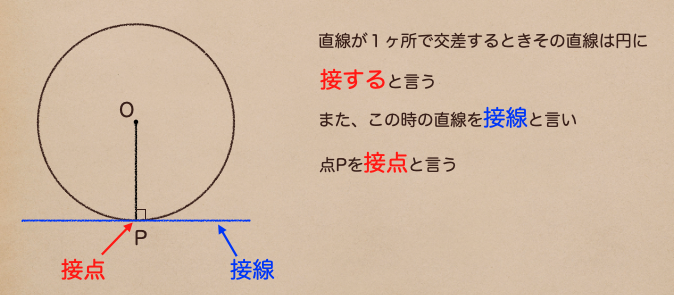
この直線が1ヶ所で交差する時の直線は円に接するって言い方をするんだね。
また、直線を接線、交点となっているところを接点って言うってことを
覚えておこう。
この接線は点OPと垂直に交差するんだね、ようするに
円の接線は、接点を通る半径に垂直
ってことになるんだ。
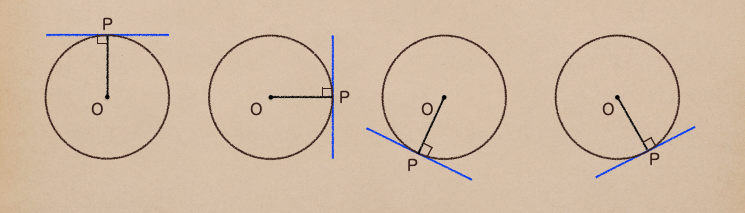
今回の図では直線を円の真下に引いて説明しているんだけど、円はその位置を取っても
同じことが言えるのも特徴の1つになるから、どの角度で接線を引いても
同じことが言えるってことも覚えておこうね。
次はおうぎ形についてやっていくよ。
おうぎ形
まずは、図でおうぎ形について確認してみよう。
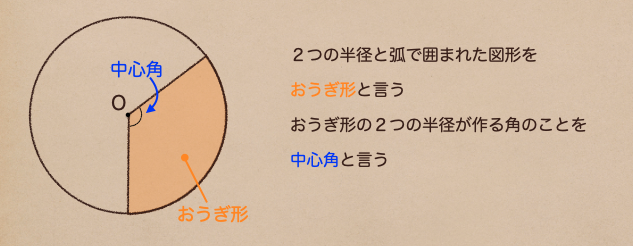
初めの方で説明した弧とその両はしから引かれた半径で囲まれた図形って言うのを
おうぎ形っていうんだね。そのおうぎ形の角度って言うのが中心角って言う言い方を
することを覚えておこう
おうぎ形っていうのは、どの形を指すのかは自由になってしまうので
今、上の図で表している反対側もおうぎ形と言えるんだね。
ただ、示しているおうぎ形に応じて、中心角っていうのは異なってくるので注意しよう。
おうぎ形には次の特徴もあるってことを覚えておいてね。
半径と中心角が等しい2つのおうぎ形は合同で
その弧の長さや面積は等しい
ここで出てくる合同っていうのは2つの図形を重ねあわせた時にピッタリ重ね合わせることが
言えることをいうんだね。ようするに形が同じ図形ってことだね。
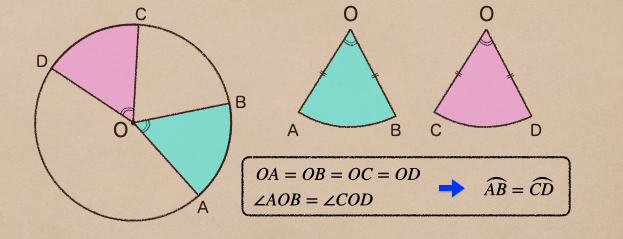
おうぎ形の特徴としてしっかり理解しておいて。
次は、円の面積についてやっていくね。
円の周の長さと面積
円の周の長さや面積っていうのは小学生で習ったから覚えてるよね。
一度、確認しておこう
円の周の長さ=直径×円周率
円の面積=半径×半径×円周率
だったよね。この円周率っていうのは円周の直径に対する割合を指しているんだけど
これっていうのが、決まった数値があって円周率=3.1415926535897932384626338……
といつまでも、割り切れない数字が続くんだけど、一般的には円周率=3.14とされているよね。
数学では、この円周率っていうのをギリシャ文字のπ(パイ)で表すんだね。
このπっていうのはこれからもずっと使われていって
π=円周率ってことを覚えておこう。
そして、このπを使って円の周の長さや、面積を表すと
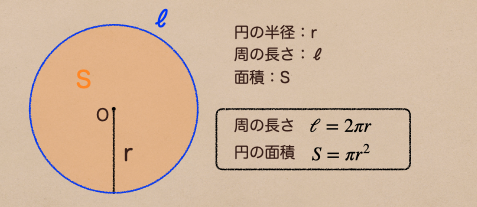
それぞれ、円の半径をr、周の長さを\(\ell\)、面積をSとした場合
周の長さ ・・・ \(\ell=2\pi r\)
円の面積 ・・・\(S=\pi r^2\)
って式で表すことができるんだね。
この式で使われている、円周率\(\pi\)や半径 r って言うのはこれからの数学では
よく使われるから円周率は\(\pi\)、半径は r って覚えておこう
ちなみに直径は大文字のRでよく表されるよ。
この、円の周の長さ・面積をふまえて次はおうぎ形の弧の長さ、面積について
やっていくよ。
おうぎ形の弧の長さと面積
おうぎ形の弧の長さや面積って言うのは、こんなふうに考えればわかるかな。
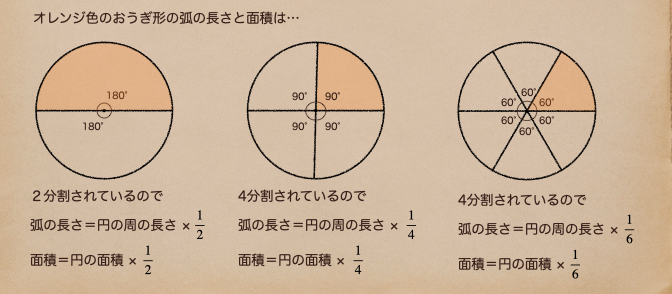
上の図のようにわかりやすく円を分けた場合のおうぎ形の弧の長さ、面積は
円の周の長さ、面積に分けている分で割ってあげれば計算できるよね。
ここで、注目したいのは、2分割されている時のおうぎ形の中心角は180°になってるよね。
これって、円の角度360°から見ると半分だよね。
同じく、4分割の場合、6分割の場合を見ると同じようにそれぞれのおうぎ形の中心角と
円の角度との関係が同じであることに気付いたかな。ようするに
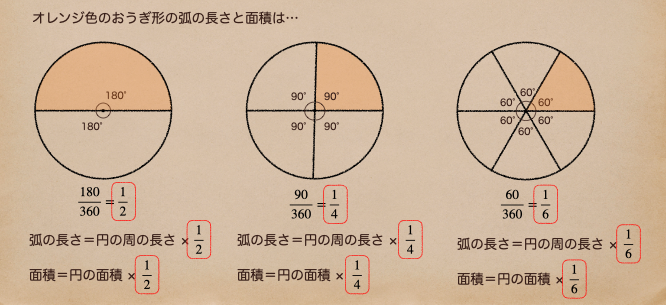
すべて、おうぎ形の中心角 ÷ 円の角度 で計算された分数を円の周の長さと面積に
かけることでおうぎ形の弧の長さと面積っていうのが計算できてるよね。
このことからおうぎ形の弧の長さと面積の求め方は…
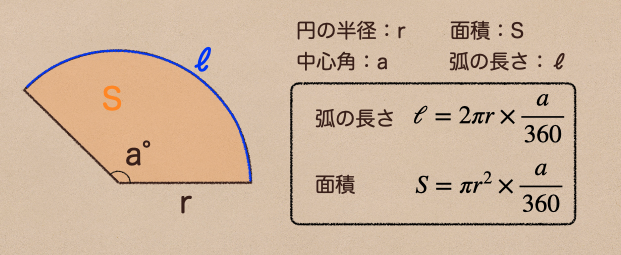
円の周の長さと面積におうぎ形の 中心角/360° をかけてあげれば
おうぎ形の弧の長さと面積が求められるってことだね。
求め方がわからなくなったり、忘れてしまったりした場合は
円の2等分したおうぎ形や4等分したおうぎ形を思い出してみてね。
円の2等分ってことは\(\frac{1}{2}\)だから\(\frac{中心角}{360°}\)ってことを
思い出しやすくなるよ。
ただ、ここでしっかり覚えていかないといけないのは、円の周の長さと面積に
ついてだね。これを覚えていないとおうぎ形の弧の長さや面積も
求められなくなっちゃうからね。
あともう1つ、覚えておいてほしいことがあるんだ。
それは、1つの円ではおうぎ形の弧の長さや面積の比って言うのは
中心角の大きさに比例するってことなんだ。ようするに
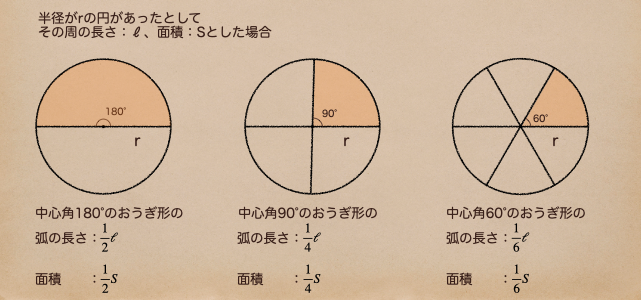
おうぎ形の弧の長さがそれぞれ、\(\frac{1}{2}\ell\)、\(\frac{1}{4}\ell\)、\(\frac{1}{6}\ell\)で表すことができて
面積も同じように、\(\frac{1}{2}S\)、\(\frac{1}{4}S\)、\(\frac{1}{6} S\)で表すことができるよね
ここで、弧の長さの比は\(\frac{1}{2}\ell\):\(\frac{1}{4}\ell\):\(\frac{1}{6}\ell\)ってなって
これを簡単にすると 6 : 3 : 2 となるよね。
同様に面積の比も\(\frac{1}{2}S\):\(\frac{1}{4}S\):\(\frac{1}{6} S\)ってなって
これも簡単にすると 6 : 3 : 2 となるよね。
今度は、中心角の比を見てみると 180° : 90° : 60° となるよね。
これも簡単にして表すと… 6 : 3 : 2 となって
弧の長さの比や面積の比と同じになるよね。これが、
1つの円ではおうぎ形の弧の長さや面積の比は
中心角の大きさに比例する
ってことなんだ。
また、円のおうぎ形の長さや面積の関係っていうのは比例式で表すと
半径の等しい円とおうぎ形は
(おうぎ形の弧の長さ):(円の周の長さ)=(中心角の大きさ):360
(おうぎ形の面積):(円の面積)=(中心角の大きさ):360
ってことになるんだね。
こういった感じで、おうぎ形と円って言うのは、大きく関わっているってことになるから
しっかり、理解しておこう。
ちなみに、円のおうぎ形が関係する時っていうのは半径が等しいってことが
ポイントになるので、気をつけよう。
はい、ではここまでが平面図形(3)円とおうぎ形についてでした。
ここまでの記事が良かったと思ったらここをクリックしてね。
質問なんかがあった場合はコメントにお願いします。
では、またさようなら。





コメント