どうも、こんにちはDKです。
今回は平面図形の基礎をやっていきます。
今までは、正負の数、方程式、関数と計算や文字を使った式だったんだけど
今回の平面図形では、図形を使ったものになるよ。
これはこれで、図形問題苦手って人も多いと思うんだけど、中学1年生で習う図形は
ほんと、基礎の説明を行なっている所になるんだけど、この基礎を理解しないままに
進んでしまうと、いっきについていけない(理解できない)ってことになっちゃうから
ここで、しっかり図形に対する基礎を身につけていこう。
動画でも方程式の基礎を公開しているのでこちらも見てみてください。
※音が出るので、周りに気をつけて再生してみてね。
じゃあ、早速やっていくね。
直線と図形
この直線と図形では、図形におけるそれぞれの呼び方(記号)について説明しているよ。
ここの呼び方(記号)は図形の表し方としてよく使われるものになるからしっかり覚えておいてね。
直線と角
今までにもよく使われていた『直線』って言葉だけど、これを正しく理解しているかな?
この『直線』って言うのは実際はこう言うものを指しているんだね。
直線:まっすぐな線、限りなく伸びている線
まっすぐな線っていうのはわかるよね。曲がっていたり、折れていたりする線は直線じゃないもんね。
けど、『限りなく伸びている線』ってどういうこと?ってなるよね。
これっていうのはずっと途切れることなく続いているってことになるんだね。
実際は、教科書なんかの直線は限りなく続いている線の一部が書かれているだけで
実際は、どこまでも続いている線になっているってことなんだね。
じゃあ、途中で途切れている線は直線じゃないってことになるんだけど
これにも呼び方があって、『線分』っていう言い方をするんだね。
点Aから点Bまで線が引かれていた場合なんかを『線分AB』なんて言い方をするんだ。
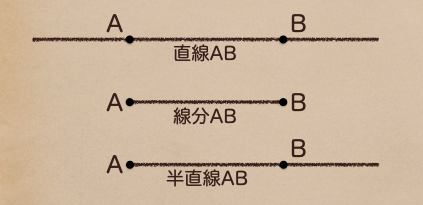
線分ABの片方だけが直線と同じように限りなく伸びている線の場合を
『半直線』っていう言い方をするっていうのも覚えておこう。
この線分っていうのは点Aから、点Bまでを結んだ線を指しているんだけど

このように線分ABは最短の長さのものを指してその長さを『AB』として表すことができるんだね。
線分ABの長さOOを AB=OO として表すこともできるんだね。
ここまでが直線についてなんだけど、直線っていうのが、まっすぐな線っていうだけじゃなくて
ここからここまでの線を線分って言ったりと、線を引くだけでも色々な呼び方があるんだね。
これからの数学ではこの言葉を使い分けていく必要があるからしっかり理解しておこう。
次は角(かく)についてなんだけど、この角(かく)って何かって言うと
角・・・1つの点から引いた、2本の半直線の作る図形
これを角って言うんだね。
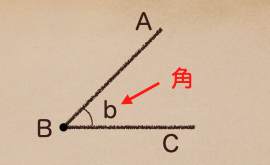
そして、この角 b を角ABCっていう言い方をするんだ。
記号で書くと \(\angle\mathrm{ABC}\) ってなるんだね。
ちなみに、この \(\angle\mathrm{ABC}\) と書いた場合、アルファベットの真ん中の部分が
角になるように書く必要があるから注意しよう。

また、 \(\angle\mathrm{ABC}\) は単純に \(\angle\mathrm{B}\) や \(\angle\mathrm{b}\) と
表すこともできるんだ。
それと \(\angle\mathrm{ABC}\) と書いて、そのまま \(\angle\mathrm{ABC}\) の大きさを
表すこともできるんだね。
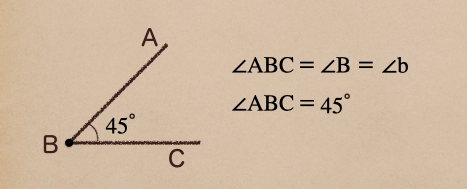
ここまでが、直線と角についてだよ。
数学ではこのように、直線、角に対しても記号で表されるとこになって、この記号を使って
問題が出題されることになるので、記号の意味や書き方なんかをしっかり理解しておくようにしよう。
垂直と平行
次は垂直と平行についてやっていくね。
まず、垂直(すいちょく)の意味はしっかり理解できているかな?
垂直っていうのはこう言うことだったよね
垂直・・・2つの直線が交わっており、その角が直角である
これが、垂直だね。 さっき習った、角となる部分が直角(90°)となっていた場合
垂直になっているってことになるんだね。
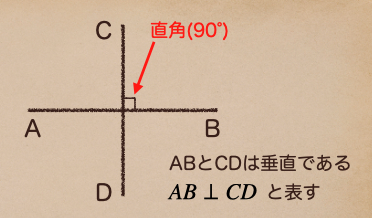
上の図のように直線ABと直線CDの交わっている点(交点)が直角(90°)である時を
言うんだね、そしてこの垂直を表す記号っていうのが \(AB\perp CD\) って書くことで
ABとCDは垂直ですって言ってるんだね。
この垂直記号 \(\perp \) は特別な読み方はないのでそのまま『すいちょく』と
読めばいいからね。
この\(AB\perp CD\) は『ABはCDに垂線』『CDはABに垂線』っていうことができて
垂線(すいせん)っていうのは、垂直になる線のことを言ってるんだね。
この垂線っていうのが、点と線の距離(長さ)を表すのに大事になってくるんだ。
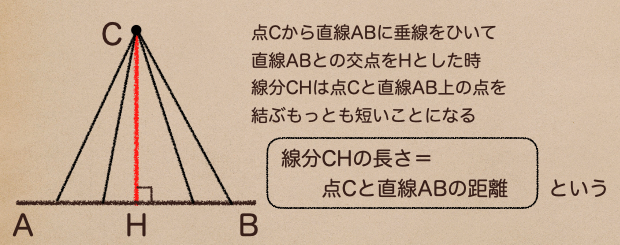
上の図で言っているのが、点Cから直線ABに対していくらでも線分をひくことができるよね、
けど、この点Cから直線ABまでの長さを表したい時っていうのは
点Cから垂直にひいた線を言うってことだね。
垂直と平行のもう一つ、平行についてやっていくね。
平行っていうのも小学生でも習ったかと思うんだけど、意味も含めて確認しておこう。
平行・・・2つの直線が交わることがない状態
平行って言うものを2つの直線と言っているんだけど、この直線の定義って覚えてるかな?
直線っていうのは、限りなくまっすぐな線だったよね。
要するに平行って言うのは、どこまで行っても交わることのない2つの直線ってことだね。
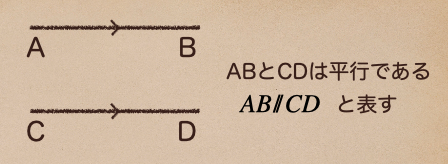
図の場合は、直線に『<』のような記号を書くことで、ABとCDは平行って言うのを表しているんだ。
記号で書く場合は、\(AB/\!/ CD\) ってなってこれで、ABとCDは平行って言っているんだね。
平行である直線に対して、次のような特徴もあるんで、覚えておこう。
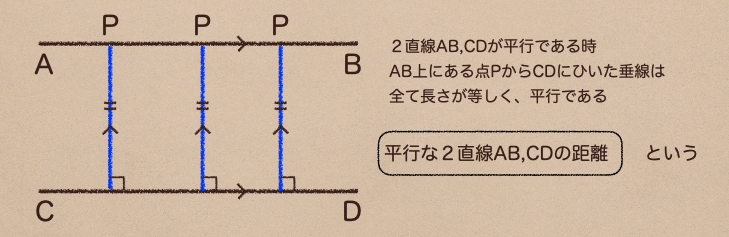
平行な直線どうしにひかれた垂線(線分)はどこに線分をひいても、長さが等しいってことだね。
また、その線分どうしも、平行ってことだよ。
垂直と平行は小学校でも習ったことあるから、どう言うことはわかっていると思うけど
もう一度、正しく意味を理解しておこう。
ここで、大事なのは、記号での表示の仕方と、それぞれの長さ(距離)の取り方だね
図形での、距離っていうのは、基本的にはもっとも短い線の長さをその距離として
表していることになるんだ。
多角形
今度は、多角形について説明していくね。
まずは多角形とは?って言うところを理解しておこう。
多角形・・・いくつかの線分で囲われた図形
いくつかのって言い方をしているけど、実際は3つ以上の線分になるね。
2つの線分では、囲うことができないから多角形とはならないってことだね。
多角形には色々あって…
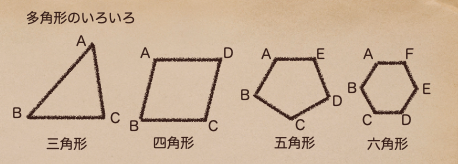
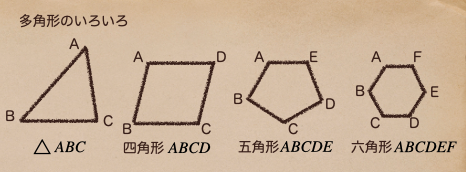
三角形、四角形・・・と多角形はいろいろな図形があるんだね。
この三角形、四角形・・・といろいろある図形の中で、何角形の図形かを判断したい場合は
辺の数(線分の数)もしくは、角の数がいくつか見れば、何角形かはわかるよ。
上の図の場合も、辺が3つ(角が3つ)で三角形、辺が4つ(角が4つ)で四角形って
なってることがわかるよね。
この多角形で各頂点(角となるところ)には記号A,B,C・・・があるんだけど
この多角形の中で、三角形だけは記号で表すことができるんだね。
それが \(\triangle{ABC}\) って書くことで三角形ABCを表しているんだね。
他の多角形に関しては、記号で表す必要はなく単純に四角形ABCD、五角形ABCDEの
ように書き表したらいいからね。
今回は、この中でも、三角形の図形に関して特徴を説明しておくね。
三角形で押さえておきたいポイントは正三角形と二等辺三角形になるんだ。
正三角形は3つの辺が全て等しく、3つの角は全て等しいだったよね。
二等辺三角形は2つの辺が等しく、その辺の角は等しいってことだね。
ここは、これらの特徴を式、記号で表した場合はこうだね。
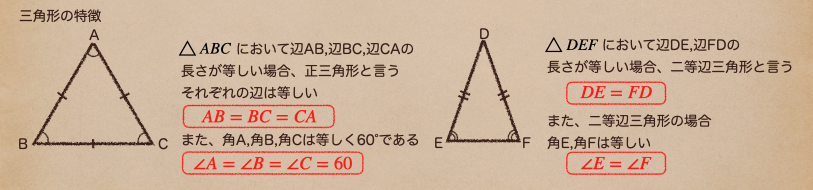
この、記号で表すことや等式っていうのは、今後、よく使われていくことにもなるから
しっかり、覚えておこう。
それと、これらの特徴を満たしている場合はそれぞれ正三角形、二等辺三角形で
あるってことになるんだね。
なので、3辺が等しい三角形や3つの角が等しく三角形って言われたら正三角形だって
わかるってことだね。
ここまでが平面図形の基礎となる部分で、言葉や記号を覚えることがメインになってしまうけど
この記号の表し方を理解できてる、できていないで差がついちゃうから理解しておこう。
次は、図形の移動についてやっていくよ。
図形の移動
図形における移動についてやっていくよ。
まず、この図形における『移動』っていうものについてしっかり理解しておこう。
移動・・・図形を形、大きさを変えずに、他の位置に移すこと
形、大きさを変えないっていうところが、ポイントだよ。
また、移動によって移った点と、元の位置にあった点とを対応する点って言い方をするよ。
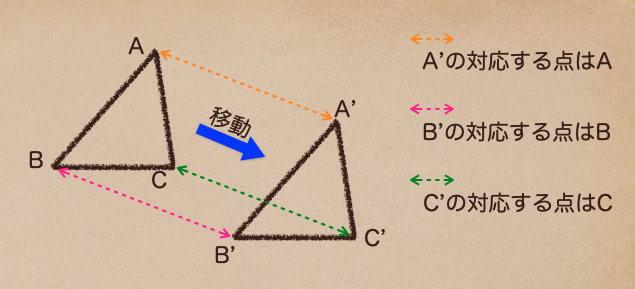
ここからはいろいろな移動について説明していくね。
平行移動
平面上の図形を一定の方向に一定の長さだけ移すこと
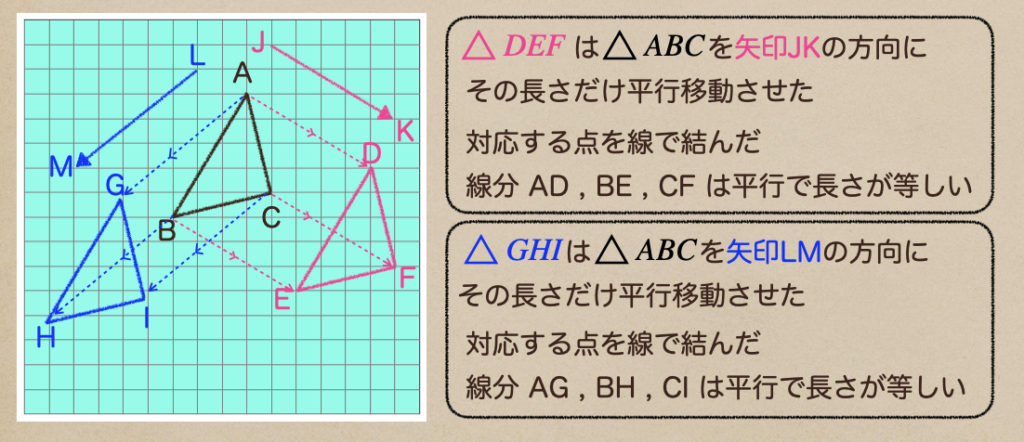
平行移動には上記のような特徴があるんだね。
特に対応する点を結んだ線分は平行で長さが等しいっていう特徴をしっかり理解しておこう。
回転移動
平面上で図形を1つの点を中心として、一定の角度だけまわして移すこと
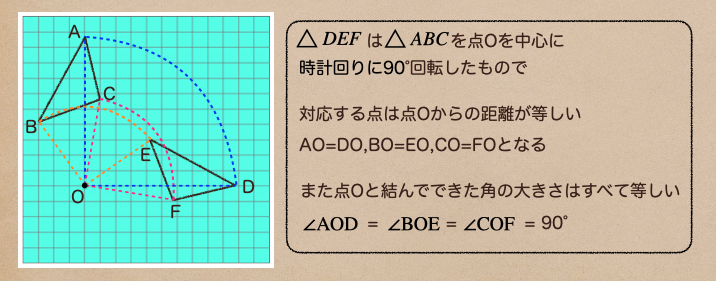
この回転移動は中心となる点Oがどこにあるかによって、回転した時の対応する図形の位置も
変わってくるよ。図形の中に中心Oを置くこともできるので、いろいろな位置に中心点を
おいてみてどのような移動図形ができるか確認してみよう。
上の図で点Oと結んでできた角の大きさを『=90°』としているんだけど
今回の図形は90°回転させているからで、60°回転させた回転図形の場合は『=60°』って
なるから、等しくなる角は移動した回転角度によって変わるってことを覚えておこう。
回転移動の中でも、回転角度を180°回転させた時は特別、こんな呼び方をするんだ。
点対称移動
180°の回転移動を行なうこと
180°の回転移動した場合が下の図のようになるんだね。
これを点対称移動と言って、点を対称に移動したってことになるんだね。
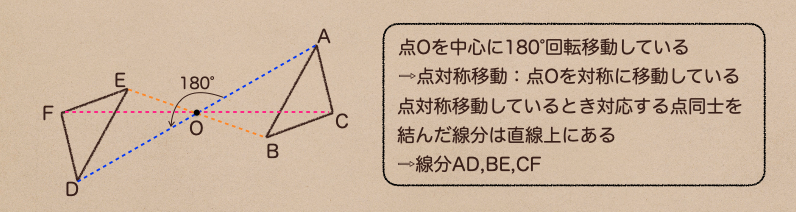
回転移動っていうのは、回転する角度によって、対応する点同士を結んだ線分は
回転する角度と同じになるんだけど、点対称移動の場合は回転する角度が180°なので
対応する点同士の線分っていうのは180°になるよね。それって直線上にあるってことなので
点対称移動の場合は対応する線分が1つの直線上にあるよってことになるんだね。
対称移動
平面上の図形で1つの直線を折り目として、折り返して移すこと
対称移動は直線に折り返して移動するってことなんだけど、少しイメージしにくいよね。
おりがみを半分に折って、ハサミで切り抜いた後に、おりがみを開いた時に折り目と対称に
同じ形ができるよね。これが対称移動したのと同じことになるんだ。
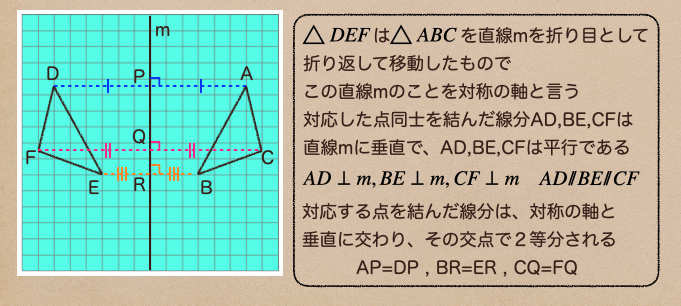
対称移動した時の対応する点同士が対称の軸で2等分されるって言うところは
ポイントとなるから覚えておこう。
この対称の軸っていうのは、下の図のようにも言えるんだね。
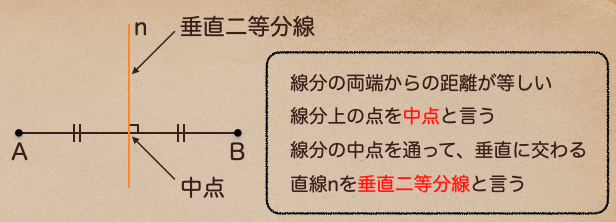
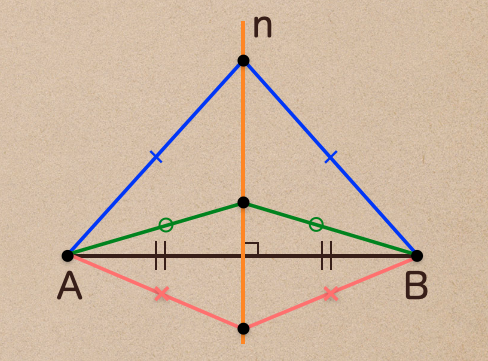
この垂直二等分線っていうのが、対称の軸を指していて
点Bは点Aを直線nで対称移動したものってことになるんだね。
この垂直二等分線上にある点とそれぞれ、点A、点Bを結んだ線分は
全て等しくなるって言う特徴もあるから覚えておこう。
ここまでが、平面図形の図形と移動についてになります。
しっかり、理解できたかな?もし、まだ自信がないようならもう一度
見直して、わからないをわかるようにしてから、次に進むようにしよう。
では、今回はここまで。
ここまでの記事が良かったと思ったらここをクリックしてね。
質問なんかがあった場合はコメントにお願いします。
では、またさようなら。




コメント