どうも、こんにちはDKです。
今回は空間図形の続きで表面積と体積についてやっていきます。
立体の表面積、体積っていうのは、公式として決められた計算式があるんだけど
その公式がどうしてそうなっているのかっていうのを説明していくね。
公式だけで覚えるっていうのも、手っ取り早くていいと思うんだけど
なぜ、こうなっているのかっていうのを理解すると公式を
わざわざ覚えていなくても、求め方っていうのがわかるようになるよ。
角柱、円柱の表面積
角柱、円柱の表面積について動画も公開しているよ。(注:音が出るよ)
角柱と円柱の表面積をやる前に、表面積って何?ってところを確認しておこう。
面積っていうのは聞いたことあるよね、じゃあ、表面積っていうのは
どう言ったものを指しているのかな?
平面図形で面積っていうと、その平面の広さの大きさっていうのを表しているんだね。
じゃあ、立体ではどうなるかな?
立体は平面、曲面で囲われていることになるよね。
なのでこの複数ある平面、曲面それぞれに面積があって、そのすべての面積を足してあげた
面積っていうのが立体の表面積っていう言い方をするんだね。
表面積・・・立体の表面全体の面積
立体の表面積は全体を表しているんだけど、他にも底面積、側面積って言う
言葉もあって、これって言うのが…
底面積・・・1つの底面の面積
側面積・・・側面全体の面積
ってことになるんだね。
ここで、注意しておくのは、底面積っていうのは底面1つ分の面積だけになるんだけど
側面積っていうのは、側面すべての合計の面積を表しているってことだね。
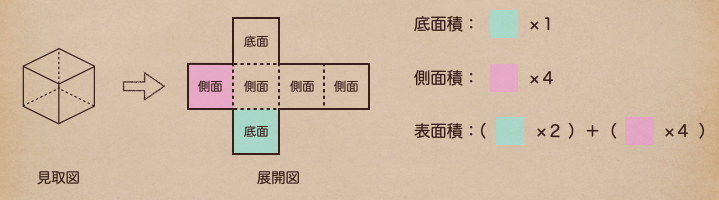
上の図のように底面積は1つ分、側面積は側面すべてになるんだね。
じゃあ、角柱、円柱の表面積はそれぞれどうなるかって言うと…
角柱の場合 ・・・ 表面積 = ( 底面積×2 )+ 側面積
円柱の場合 ・・・ 表面積 = 底面積 + 側面積
表面積はわざわざ、底面積、側面積にしてから計算する必要はないんだけど
底面積、側面積から表面積を計算する場合は注意しておこう。
それぞれ、角柱と円柱の表面積を実数を使って見てみよう。
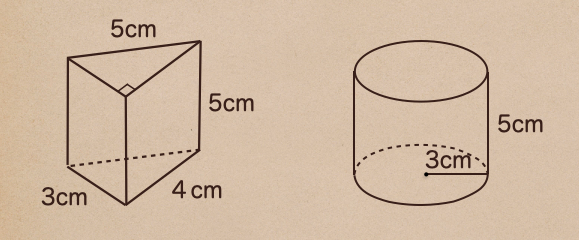
上の2つの立体に長さがそれぞれ書かれているね、この立体の底面積、側面積、表面積を
計算してみよう。まずは三角柱から見てみるね。
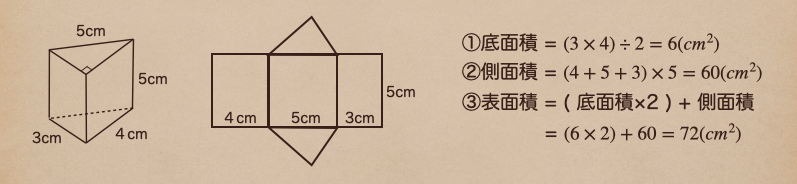
表面積を計算するときは、わかりやすくするため展開図にするして考えるのもありで
今回は展開図を表して、見てみるね。
まずは、①底面積になるんだけど、これは三角形になっているところで
底辺3cm、高さ4cmの直角三角形になっているよね
なので底面積は\(6cm^2\)になるってことだね。この底面積は1つの底面の面積になるよ。
次は②側面積だね。これは側面全体の面積になるので、それぞれの側面の底辺である
4cm、5cm、3cmを足して1つの長方形として見て
底辺×高さを計算して\(60cm^2\)ってことだね。
最後に③表面積は全ての平面の合計ってことだから(底面積×2)+側面積ってことだね。
なので、\(72cm^2\)になるってことだね。
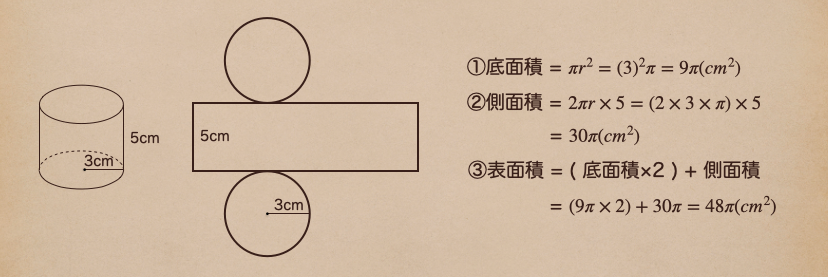
次は円柱だね。これも同様に展開図を書いてそれぞれの面積を求めてみよう。
①底面積は半径3cmの円の面積を求めればいいって事で
円の面積の公式【\(\pi r^2\)】で計算すれば求められるよね、なので\(9\pi cm^2\)。
②側面積は側面となっている長方形の面積を求めればいいよね。
高さは5cmだね。底辺はって言うと、円の周の長さが長方形の底辺の長さになるから
円の周の長さの公式【\(2\pi r\)】に高さ5cmをかけてあげるって事なので
\(30\pi cm^2\)になるって事だね。
そして、③表面積は角柱と同じで底面が2箇所あるので(底面積×2)+側面積を
計算して\(48\pi cm^2\)になるってことだね。
角柱、円柱の表面積の求め方って言うのはむずかしく考える必要はなく
すべての平面の面積の合計を求めればいいってことになるよ。
角錐、円錐の表面積
角柱、円柱の表面積について動画も公開しているよ。(注:音が出るよ)
次は角錐と円錐の表面積についてやっていくね。
こっちも、角柱、円柱と同じで底面積、側面積って言うのがあるんだけど
角錐、円錐っていうのは底面は1つだけだよね。なので
底面積と側面積で表面積を表すと…
角錐、円錐ともに:表面積 = 底面積 + 側面積
になるんだね。角柱と円柱と同じように下の立体の表面積、底面積、側面積を見ていこう。
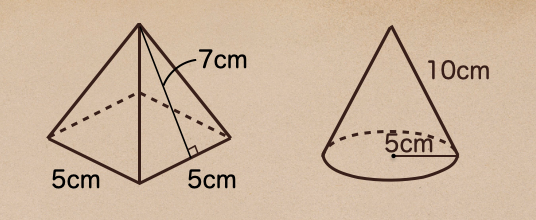
じゃあ、まずは四角錐から見てみよう。
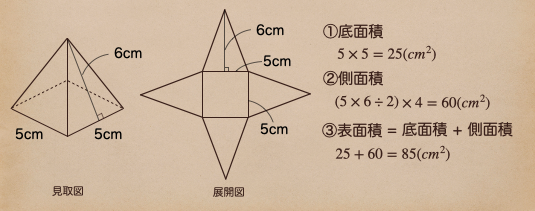
これも展開図を書いて見ていくね。
まずは①底面積は一辺が5cmの正方形になっているので
【 縦 × 横 】だよね。なので、\(25cm^2\)だね。
次は②側面積になるんだけど、角柱、円柱のときは側面積は1つに
なっていたので、縦×横で面積は出ていたんだけど、角錐っていうのは
展開図の通り、三角形になっていて、底面の辺の数だけあるよね。
ようするに三角形が4つあるって事なんで【 底辺 × 高さ ÷ 2 】で
三角形の数の分だけかけてあげて\(60cm^2\)になるってことだね。
あとは③表面積で、底面積と側面積を足してあげて\(75cm^2\)になるってことだね。
次の円錐は円とおうぎ形の面積を求めてあげるって事なので

①底面積は底面である半径5cmの面積を求めるってことで\(25\pi cm^2\)ですね。
②の側面積は少しややこしくなっているんだけど、おうぎ形の面積を求める時の
公式っていうのが【\(\pi r^2×\frac{x}{360}\)】となっておうぎ形の中心角\(x\)を
求めてあげる必要があるんだね。そこでおうぎ形の中心角を求めるために
(2π×10):(2π×5)=360:\(x\)を計算して解いてあげれば中心角\(x\)がわかるんだけど
急に比例式が出てきて❓❓ってなっちゃうよね。
この比例式っていうのは、こういうことを言っているんだね。
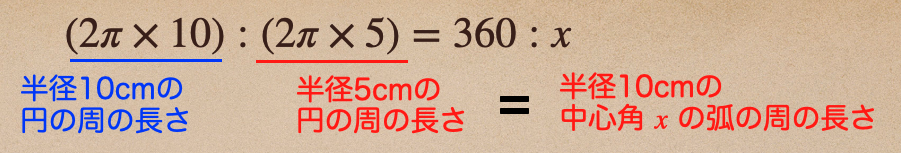
ようするに、半径5cmの円の周の長さと半径10cmの中心角\(x\)の弧の周の長さは同じで
その日は360:\(x\)になっているってことなんだね。
ここから\(x\)を求めて中心角は180°ってことがわかってあとはおうぎ形の面積を求めて
\(50\pi cm^2\)になったってことだね。
あとは③の表面積を計算してあげて\(75\pi cm^2\)になるってことだね。
円錐の側面積を求める方法は他にもあって、上で説明したのは中心角を求めて
その中心角からおうぎ形の面積を求めるってやり方だったんだけど
他にも、中心角を求めずに面積を求めるっていう方法もあるので紹介しておくね。

そのやり方っていうのが、円とおうぎ形の関係で
[おうぎ形の面積]:[円の面積]=[おうぎ形の弧の長さ]:[円の周の長さ]
っていう比例しきが成り立つってことを利用して計算しているんだね。
これっていうのは僕の平面図形(円とおうぎ形)でも説明しているから
確認してみて。ここをクリックすると平面図形の解説にいけるよ。
数学の計算方法っていうのは1つには限らず、いろいろな方向から解を導くことが
できるので、自分の得意な解き方っていうのも見つけてみるのも楽しいかもね。
角柱、円柱の体積
動画でも、解説しているよ。(注:音が出るよ)
この角柱、円柱っていうのは、立体図形(立体のいろいろな見方)で
説明していたんだけど、底面の平面を垂直な方向に平行に移動させることで
立体を作ることができているよね
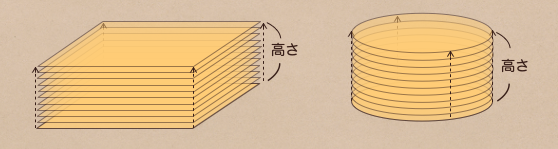
これの体積はっていうと、上の図のように重ね合わせた高さ分だけ体積が増えていく
ってことになるので、角柱と円柱の体積の求め方は 底面積 × 高さ で
求められるってことだね。
これを公式として表すと
底面積をS、高さをh、体積をVとして
\(V=Sh\)
円柱の場合、半径をrとしたとき
\(V=\pi r^2h\)
として表すことができる。ここで新しい文字がたくさん出てきているんだけど
この文字にはそれぞれ意味があって
h:height(高さ)
V:Volume(体積)
S:Square measure(面積)
r:radius(半径)
このように、それぞれを英語に直してその頭文字を使っているってことなんだね。
これからも一般的な文字と使われているため、覚えていこう。
角錐と円錐の体積
次は角錐と円錐の体積の求め方についてやっていくね。
角錐の体積っていうのは底面が同じ大きさで高さが同じ角錐の堆積っていうのは
角柱の体積の\(\frac{1}{3}\)になるんだね。
なんで\(\frac{1}{3}\)なのかっていうと
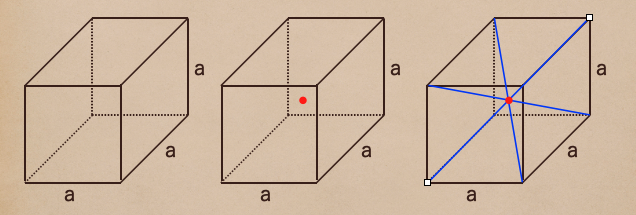
まずは、上の図の一辺がaの立方体の中心に点を置き、それぞれの角から
点に線を引くと右側の図のようになるよね。この図の中に中心に置いた点を頂点とした
四角錐って言うのが6つできているんだね。
なんで6つかって言うと立方体の底面2つに側面4つの6つの平面があるよね
その平面を底面としている四角錐ができているから6つってことになるんだね。
これを利用して下の図を見てみて。
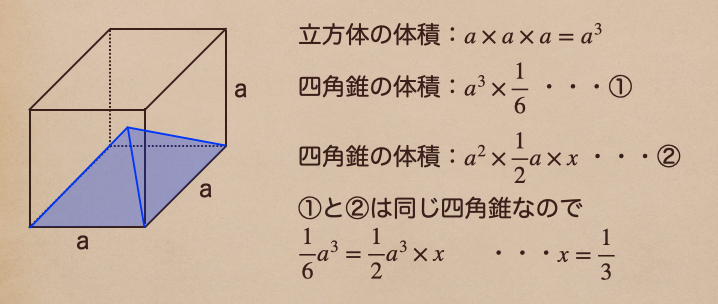
ここでは中心の点で引いた四角錐の1つの体積を見ていってみよう。
まずはさっきも言ったようにこの四角錐は立方体の体積の\(\frac{1}{6}\)ってことだったよね
なので、式①の\(\frac{1}{6}a^3\)になるよね。
そして、もう1つはこの四角錐の高さっていうのは一辺aの半分で立方体の
半分の四角柱の体積が\(\frac{1}{2}a^3\)になるよね。
これにまだわかっていない係数\(x\)をかけてあげると四角錐の体積になるんだね。
それが式②の\(\frac{1}{2}a^3×x\)ってことだね。
あとは式①と式②っていうのは、同じ四角錐なので①=②ってことで
そこから、\(x\)を解いてあげると\(x=\frac{1}{3}\)になるってことですね。
ようするに、角錐の体積は同じ底面積で同じ高さの角柱の体積の\(\frac{1}{3}\)に
なるってことなんだね。
ちなみに、こんな実験でも\(\frac{1}{3}\)はわかるみたいだよ。

底面積が同じで高さが同じ四角柱と四角錐の容器があって
この四角錐の容器に水をいっぱいまで入れて、四角柱の容器に入れていった場合
ちょうど、3杯で四角柱の容器が満杯になるんだね。
要は、四角錐の体積3つ分が四角中の体積になったってことで、体積の\(\frac{1}{3}\)に
なるってことだね。
これは円錐と円柱の間にも同じことが言えて、円柱の体積の\(\frac{1}{3}\)が
円錐の体積になるってことなんだね。
ここで、まとめると…
底面積をS、高さをh、体積をVとして
角錐の場合
\(V=\frac{1}{3}Sh\)
円錐の場合、半径をrとしたとき
\(V=\frac{1}{3}\pi r^2h\)
が、角錐と円錐の体積を求める公式になるんだね。
次は球の体積と表面積についてやっていくね。
球の体積と表面積
球の体積っていうのも、下の図のような方法で理解していこう。

半径が r の円柱の中にすっぽりと入る球があったとするよね。
この球っていうのも半径が r ってことだよね。
この球を半分にした半球の”おわん”に水を入れてその水を円柱に入れていくと
”おわん”3杯分で円柱がいっぱいになるんだね。
ようするに”おわん”の体積は円柱の体積の\(\frac{1}{3}\)ってことが言えるんだね。
このことから、球の体積を求めてみるね。

円柱の体積は[底面積×高さ]なので、底面積:\(\pi r^2\) と高さ:\(2r\) を
かけてあげればいいよね。ここで、高さが \(2r\) となっているのは球がすっぽり入る
円柱ってことだから高さっていうのは球の直径になるってことだね。
次に球の体積っていうのはまだ、わかっていないからSとして
半球の体積は球の体積の半分なので、\(\frac{1}{2}S\) だよね
そして、その半球の体積っていうのは円柱の体積の \(\frac{1}{3}\) だったよね。
なので、半球の体積と \(\frac{1}{3}\) ×円柱の体積が等しくなるってことだね。
ここから、Sを求めると \(S=\frac{4}{3}\pi r^3\) になってこれが
球の体積を求める公式になるってことなんだね。
次は球の表面積を見ていくね。
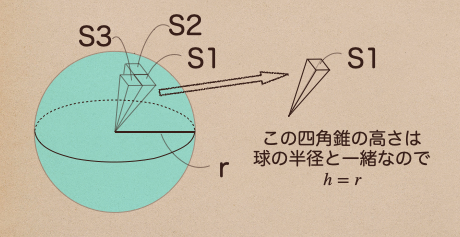
まずは上の図のように球の表面に限りなく小さくなる四角形を作って
その四角形と球の中心を線で結ぶと四角錐ができるよね。
この四角錐の底面積を\(S1\)として高さは球の半径と同じとみることができるので
\(h=r\)ってことになるよね。
この四角錐の体積はってなると \(\frac{1}{3}S1\) だよね。
この四角錐を球全体にしきつめていくと次のことが言えるんだね。

四角錐の合計の体積が球の体積になって
四角錐の底面積の合計っていうのが球の表面積になっているってことなんだね。
それを等式で表して、求めたかった表面積 \(S=4\pi r^2\) を求めたってことだね
これが球の表面積の公式になるってことだね。
まとめると
球の体積:\(V\) 球の表面積:\(S\) 球の半径:\(r\) としたとき
\(S=4\pi r^2\)
\(V=\frac{4}{3}\pi r^3\)
これが球の体積、表面積の公式になるんだけど
どうやってこの公式ができているのかっていうのを理解して公式を覚えておくのと
ただ、公式として式だけを覚えるのとでは、記憶のされ方っていうのも
変わってくるので、自分なりに理解できるところまで繰り返し見直しを
行なってみてください。
はい、ではここまでが空間図形についてでした。
ここまでの記事が良かったと思ったらここをクリックしてね。
質問なんかがあった場合はコメントにお願いします。
では、またさようなら。




コメント