どうも、こんにちはDKです。
今回は中学2年生で習う、1次関数についてやっていきますね。
中学1年生の時にも関数っていうのを習ったかと思うんだけど
基本的な考え方は同じになってくるので、1年生の関数に関して
まだ、理解できていないって人は、一度見直しを行なって
関数がどう言ったものだったかっていうのをしっかり思い出してから
ここの単元を進めていって下さいね。
ここでの解説は動画でも行なっているよ。(※音が出るから注意)
(1)1次関数
じゃあ、まずは少し復習してみましょう。
ビーカーに毎分 3ml の水を入れて \(x\) 分後の水面の高さ \(y\) mlって言うのを見ていくと。。
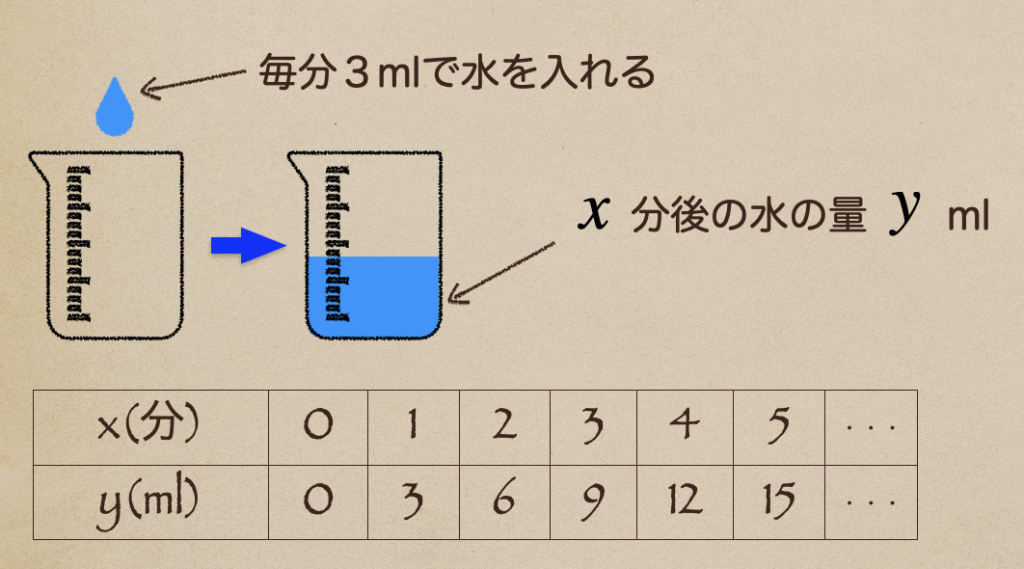
\(x\)を1分、2分・・となった時にはそれに伴って、\(y\)の値っていうのが
3ml、6ml・・と増えていってこれを関数で書くと \(y=3x\)となるって事だったよね。
これが中学1年生で習ったところで、じゃあ、今度は初めからビーカーに
4mlの水が入っているところに毎分3分の水を入れた場合にどうなるかな?
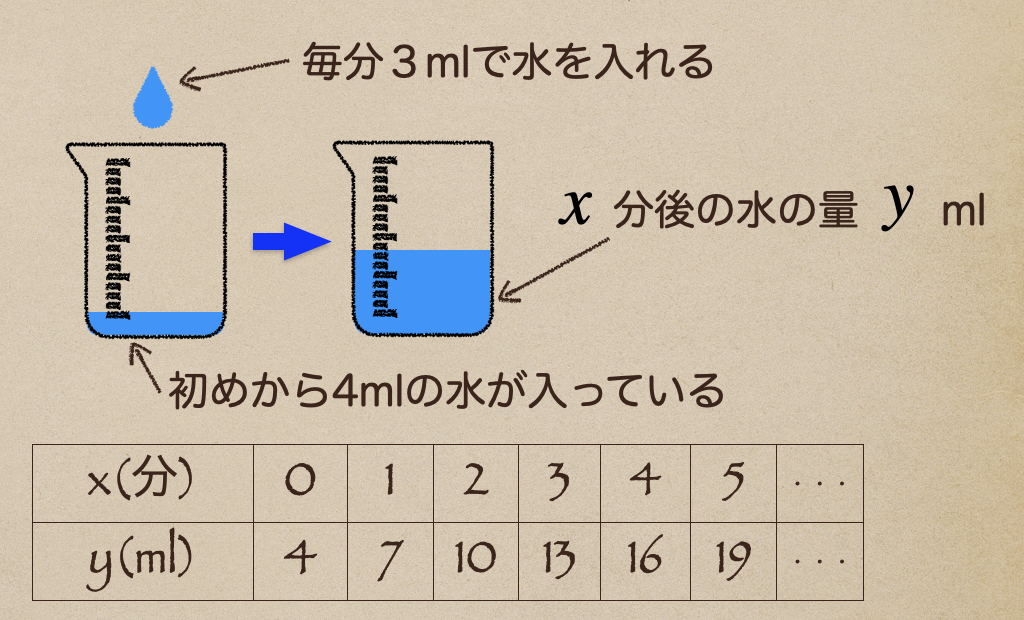
こんな風に、\(y\)の値が、4つずつ多くなっていっているのがわかるよね。
これを関数で書くと\(y=3x+4\)ってことになるんだね。この式っていうのを
\(y=ax+b\) (\(a\)、\(b\)は定数、\(a≠0\))
と表される時、\(y\)は\(x\)の1次関数である という
この1次関数っていうのは、比例する\(ax\)と定数\(b\)の和になっているってことだね。
なので、\(y=2x+3\)の1次関数で見た時、これの、\(x\)と\(y\)の値を
表にしてみてみると
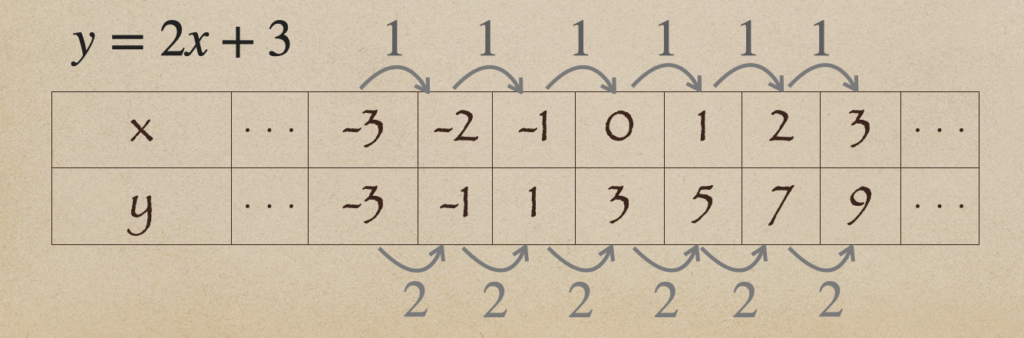
表をみてみると、\(x\)が1ずつ増えると、\(y\)の値は2ずつ増えていっているって言うのが
わかりますよね。これって言うのが。。
1次関数 \(y-ax+b\) は、\(x\)の値が1ずつ増加すると
\(y\)の値は\(a\) ずつ増えていく
なので、\(b\)の定数がどんな値だったとしても、
\(y\)の値は、\(a\)ずつ増えていくってことなんだね。
(2)変化の割合
今度は、\(x\)の値が2だったときに、\(y\)の値が9で
\(x\)の値が6だったときに、\(y\)の値が25となる時っていうのは
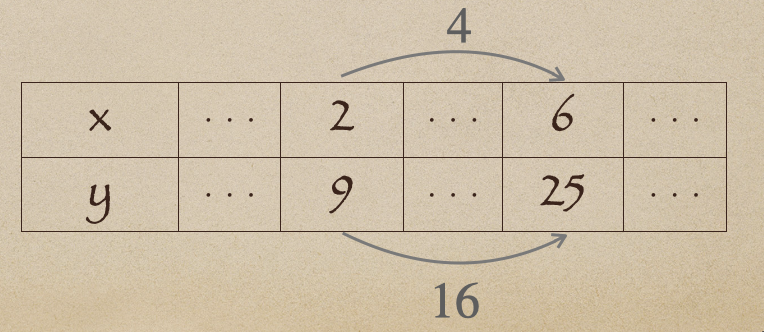
それぞれ、\(x\)の値の増加量は 4 で、\(y\)の値の増加量は 16 になってるよね。
この時の [ \(y\)の値の増加量 ] / [ \(x\)の値の増加量 ]がいくつかになるか
求めてみよう。そうすると。。 [ 〜の値の増加量 を今後は、〜の増加量と呼ぶことにする]
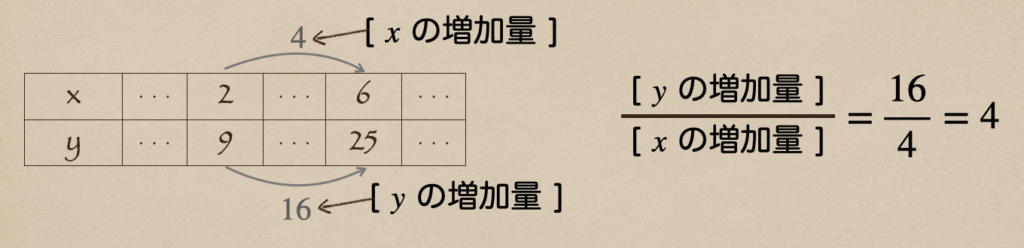
[ \(y\)の増加量 ] / [ \(x\)の増加量 ]は 4 ですってことだね。
これっていうのは、
\(x\)の増加量に対する\(y\)の増加量の割合を表している
これを、変化の割合 と言う
ってことなので、覚えておこう。
この変化の割合っていうのを1次関数で見た時、どうなっていくか考えていくよ。
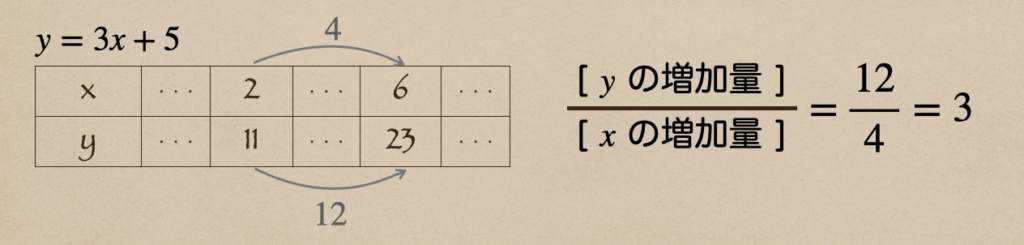
1次関数 \(y=3x+5\)があって、\(x\)の値が2から6まで増加した時
\(y\)の増加量っていうのは、12になるんだね
なので、この場合の変化の割合は3ですよってことだね。
この時、この変化の割合 3 は1次関数の\(x\)の係数と同じになっているよね。
撫のこんなことが言えるんだね。。
1次関数\(y=ax+b\)で、\(x\)の値がどんな増加量であっても
変化の割合は一定で、\(a\)に等しい
[ 変化の割合 ] = [ \(y\)の増加量 ] / [ \(x\)の増加量 ] = \(a\)
ようするに、 [ 変化の割合 ] = \(a\) ってことが言えるってことなんだね。
ここの、[ 変化の割合 ] = \(a\) っていうのは、問題なんかでもよく使われることになるので
しっかり理解しておいて下さい。
(3)1次関数のグラフ
ここから、1次関数のグラフについてやっていくね。
まずは、1次関数\(y=2x+3\)っていうのを表にすると。。
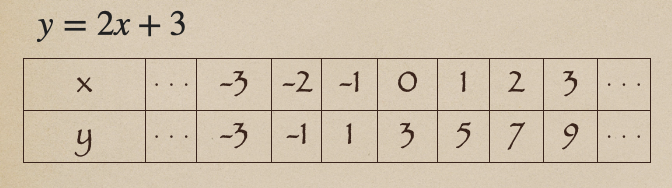
こうだね、この\(x\)と\(y\)の値の組を座標として、座標平面上においていくと

こんな風に座標点をおいていくことができるよね。
そして、この1次関数\(y=2x+3\)の点を細かくおいていくと。。
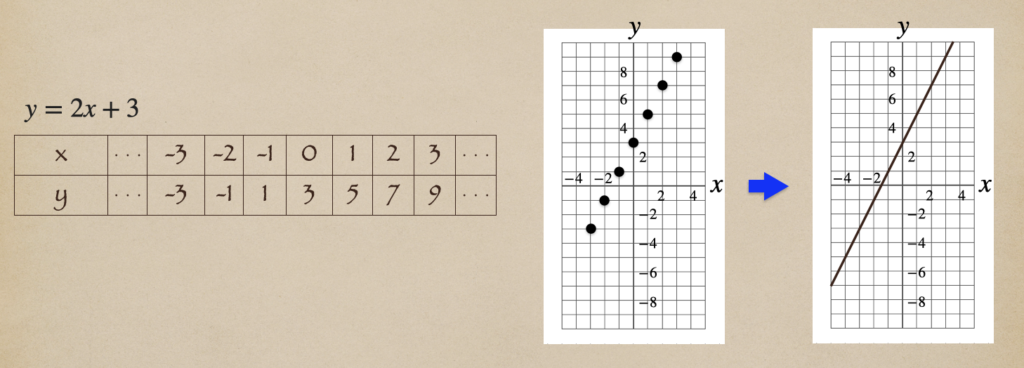
直線を引くことができて、これが1次関数\(y=2x+3\)のグラフになるんだね。
1次関数\(y=ax+b\)のグラフは\(x\)と\(y\)の値の組を
座標とした点の集合体で直線になる
ってことなんだね。
じゃあ、この1次関数\(y=2x+3\)のグラフと\(y=2x\)のグラフって言うのは
どんな、違いがあるか確認してみよう。
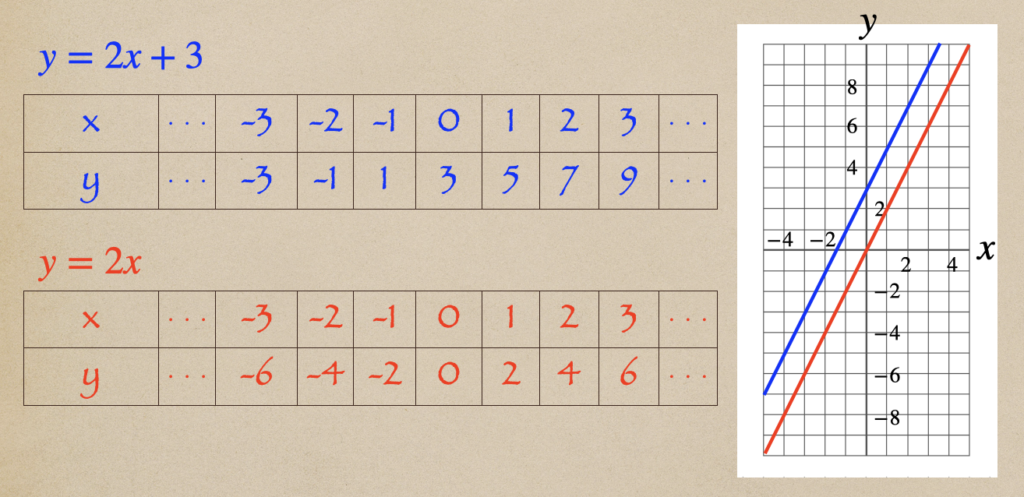
青色のグラフが\(y=2x+3\)、赤色のグラフが\(y=2x\)に
なるんだけど、この二つのグラフを見てわかるように
二つのグラフは平行になっているよね。
これって言うのが、
1次関数\(y=ax+b\)のグラフは\(y=ax\)のグラフを\(y\)軸方向に
\(b\)だけ平行移動させたもの
1次関数\(y=ax+b\)でそれぞれ、\(a\)と\(b\)には、呼び方があって
\(a\)を傾き、 \(b\)を切片(せっぺん)と言うので、これも覚えておいてね。
\(a\)=[傾き]=[変化の割合]
ってなるので、ここも覚えておいてね。
次は1次関数のグラフの特徴について確認しておくね。
1次関数\(y=ax+b\)のグラフは傾き\(a\)、切片\(b\)の直線である
\(x\)の値が1増加したら、\(y\)の値は変化の割合と同じだけ増加する
これが特徴になるんだね。
『\(y\)の値は、変化の割合と同じだけ増加する』ってあるけど
なんか、わかりにくい言い方をしているよね。
これは下のグラフを見てみて。
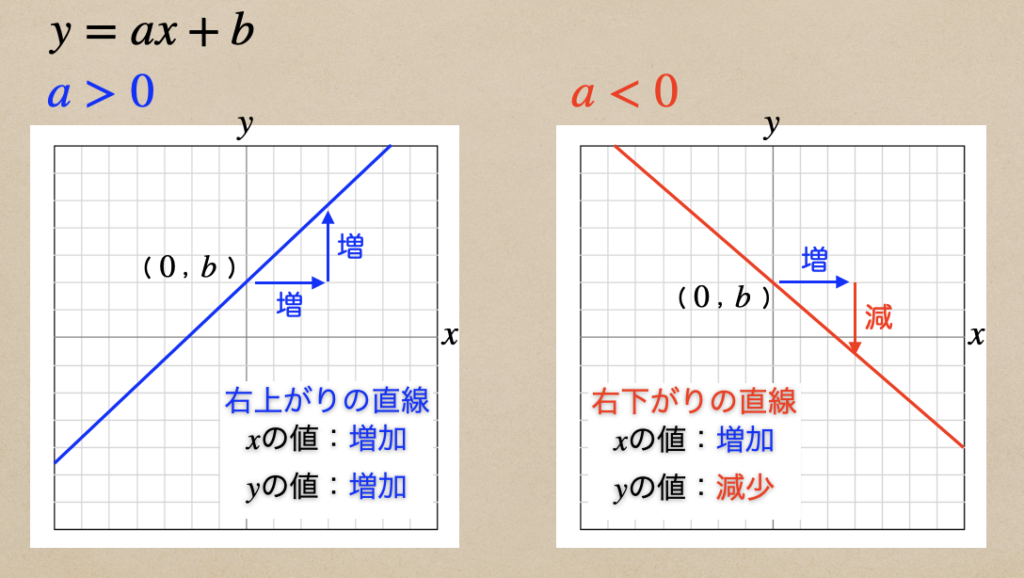
1次関数\(y=ax+b\)があって、
\(a>0\) 正の数の時は\(x\)が1増加すれば、\(y\)は\(a\)増加して・・右上がりのグラフ
\(a<0\) 負の数の時は\(x\)が1増加すれば、\(y\)は\(a\)減少する・・右下がりのグラフ
になるってことを言っているんだね。
この、右上がり、右下がりっていうのは中学1年の関数でも、出てきた内容で
1次関数のグラフも比例のグラフも特徴は同じってことになるね。
あと、上のグラフのことを、直線\(y=ax+b\)と言うよ。
(4)1次関数のグラフの書き方
1次関数\(y=-2x+3\)をグラフで書きたいってなった場合のやり方を
説明しておくよ。
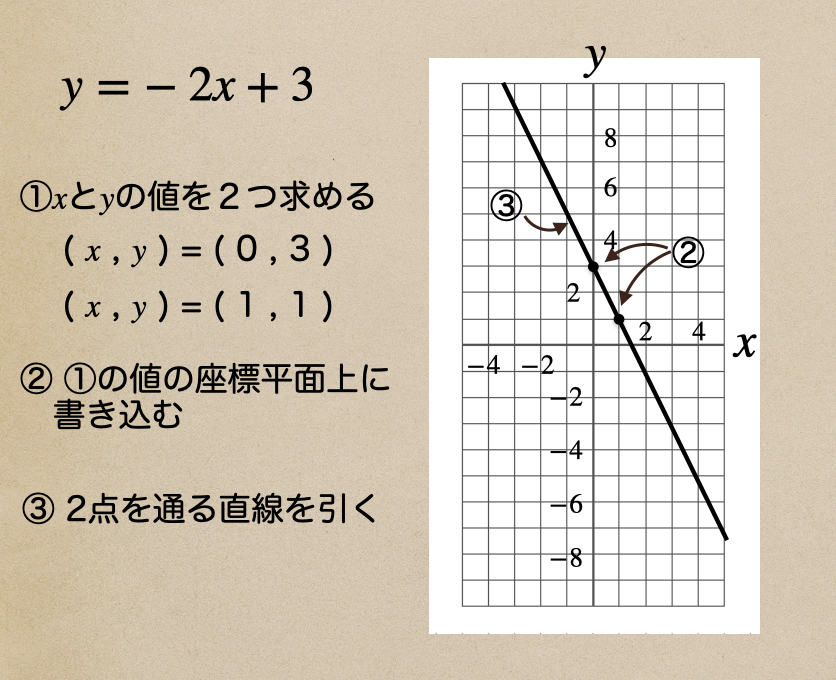
グラフを書くときは、\(x\)と\(y\)の値の組を2つ求めて
それの座標点を書き込んで、その2点を通る直線をひけば
グラフが書けるってことだね。
(5)1次関数の式の求め方
今までは1次関数の式っていうのがわかっていたよね。
そこから、グラフを書いていってたんだけど、今度は
1次関数がわかっていない場合の式を求めていく方法を見ていきますね。
①グラフから式を求める
これはグラフから1次関数の式を求めるってことだね。
例えば。。
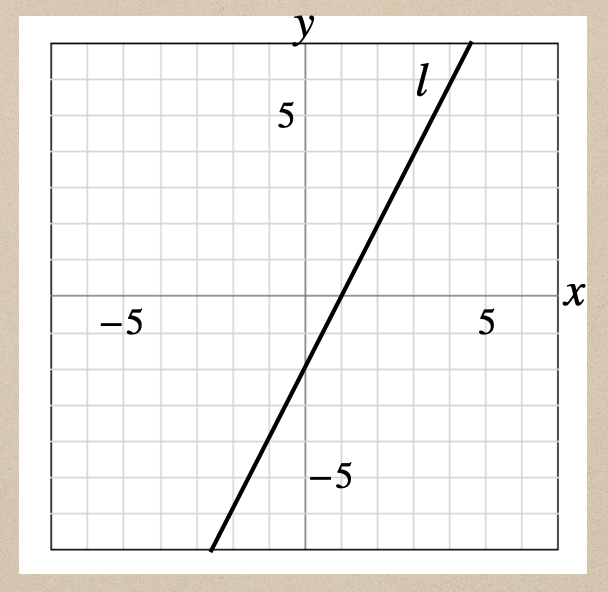
この直線\(l\)の1次関数の式を求めたいってなった時は
傾きと切片がわかると1次関数の式を求めることができるんだね。
グラフから傾きと切片を見てみよう。
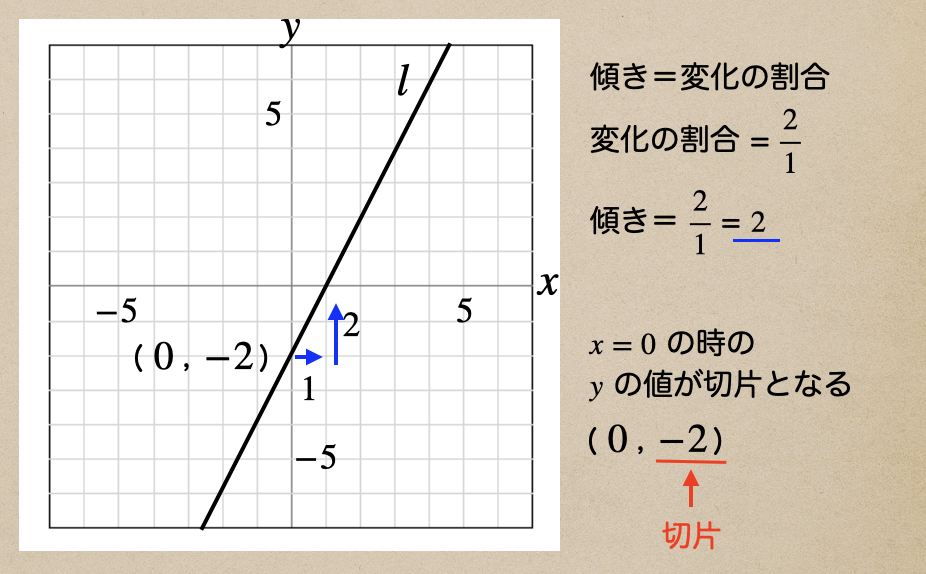
傾きって言うのは、変化の割合だったよよね。
変化の割合は[\(y\)の増加量] / [\(x\)の増加量]ってことのなので
傾き = 2になるってことだね、そして、切片はグラフの\(y\)軸上の点の\(y\)の値のことになるので
切片 = -2となるね。これで傾きと切片がわかったので、これから1次関数の式を
作ってあげればいいってことだね。1次関数\(y=ax+b\) ( \(a\):傾き , \(b\):切片 )
このグラフの1次関数の式は、\(y=2x-2\) になるってことだね。
②条件から式を求める 1
変化の割合がわかっていて、\(x\)と\(y\)の値がわかっていた場合でも
1次関数の式を求められるってことだね。

これが
傾きと、その直線が通る1点が分かれば
1次関数をこ求めることができる
って、ことになるのでここも、求め方っていうのを理解しておこう。
③条件から式を求める 2
\(x\)と\(y\)の値の組が2つわかっている時の1次関数の求められるんだね。
( \(x\)、\(y\) ) = ( 1 、7 ) 、( \(x\)、\(y\) ) = ( 3、13 ) を通る直線の
1次関数を求めてみよう。

2つの座標点がわかっていることで、変化の割合っていうのを求めることが
できるよね。
変化の割合が求めれれば、それが傾きになるってことだったよね。
あとは、どちらかの座標点を代入してあげて、切片を求めてあげれば
1次関数の式を作ることができたね。
こんな風に、いろいろな条件で1次関数を求めることができるので
しっかり、理解しておこう。
今回は、ここまでになります。
ここまでの記事が良かったと思ったらここをクリックしてね。
質問なんかがあった場合はコメントにお願いします。
では、またさようなら



コメント
ええですねえ