どうも、こんにちはDKです。
ここでは、中学生で習う数学の基礎を解説しているよ。
今回は中学2年生で習う、『三角形と四角形』についてになるよ。
ここでは、「三角形」についてで、小学校から習ってきた当たり前の図形である三角形を
ここまでに習ってきた、証明を用いて、この三角形はこんなことが言えるよって
ことを正しく理解しておこう。
これから学ぶ人は予習として、一度、学んだことのある人は復習に
活用してみてください。
動画でも基礎の解説を行なっているので、そちらも見てみて下さい
(動画は音が出るので注意して)
解説に入っていく前に、三角形っていろいろな形があったよね。
下の①から⑥の三角形を見ておさらいしておこう
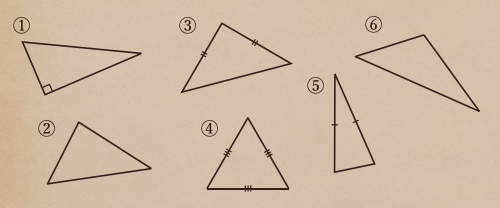
①は1つの角が直角になっているよね、これっていうのは「直角三角形」って言うんだったよね。
③や⑤の三角形は、2つの辺が等しい三角形になってるね。こんな形の三角形を
「二等辺三角形」って言ってたね。
④は3つの辺が等しいってことになっているので、「正三角形」ってことだね。
あと、残りの②や⑥は特に特徴のない形になっているので普通の「三角形」ってことだね。
こんな風に三角形にも、いろいろな形があって、それぞれに特徴っていうのがあるよね。
この三角形の中で、まずは③や⑤の二等辺三角形に注目してみるね。
(1)二等辺三角形の性質
さっきの図形の中で、③や⑤っていうのをなんで「二等辺三角形」って言ったかっていうと
それっていうのは、2つの辺が等しい三角形だから、「二等辺三角形」です。って
言っていたよね。こんな風に
図形が二等辺三角形かどうかっていうのは「二等辺三角形」の意味をはっきりさせておく必要があって
これっていうのは、その用語(ここでは二等辺三角形)を誰が説明しても
同じ意味になるようにしないといけないんだね。
その用語の意味を簡潔に述べたものっていうのを、その用語の定義(ていぎ)って言い方をするんだ。
なので、この「二等辺三角形」の定義はっていうと
二等辺三角形の定義:2つの辺が等しい三角形
ってことになるんだね。
この条件を満たしている三角形は、二等辺三角形ですよってことが言えるってことになるんだね。
この二等辺三角形で角や辺には呼び方があって
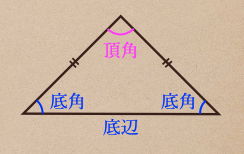
等しい2つの辺の間の角を頂角(ちょうかく)と言って
頂角に対する辺を底辺(ていへん)で底辺の両端の角を底角(ていかく)って
呼び方をするので、今後は二等辺三角形ではこの呼び方をしっかり覚えておいてね。
ここからは、二等辺三角形はどんなことが言えるのかっていうのを確認していってみよう。
まずは、二等辺三角形の頂角を二等分する線分を引いて、底辺のBCとの
交点をDとした図形の\(\bigtriangleup ABD\)と\(\bigtriangleup ACD\)が合同であることを
証明してみよう。

ここで、図形の証明になるので、仮定と結論は。。
仮定:\(AB=AC\)、\(\angle BAD=\angle CAD\)
結論:\(\bigtriangleup ABD \equiv \bigtriangleup ACD\)
ってことだね、これらから証明をしていくと。。

これで、\(\bigtriangleup ABD\)と\(\bigtriangleup ACD\)が合同ってことが
言えたよね。
そして、合同な図形の性質から「対応する角の大きさはそれぞれ等しい」っていうことから
\(\angle ABD=\angle ACD\)ってことが言えるよね。

これっていうのが、さっきの二等辺三角形の角の呼び方で言うところの底角ってことになるよね
ようするに、二等辺三角形の底角っていうのは、等しいですってことが
今回の証明で言えたってことになるんだね。
この、底角は等しいってことは二等辺三角形の性質ってことになるんだけど、
この性質の中でも特に重要なことがらっていうのを定理(ていり)っていう言い方をするんだね。
[二等辺三角形の性質]
定理:二等辺三角形の2つの底角は等しい
この定理っていうのは、
すでに証明されたことがらで、他のいろいろな証明をするための
根拠としてよく使われるもの になるので、この定理っていうのは
しっかり、理解しておくようにしよう。
さっきの\(\bigtriangleup ABD \equiv \bigtriangleup ACD\)ってことから
残りの\(\angle ADB\)と\(\angle ADC\)に注目して、見てみよう。
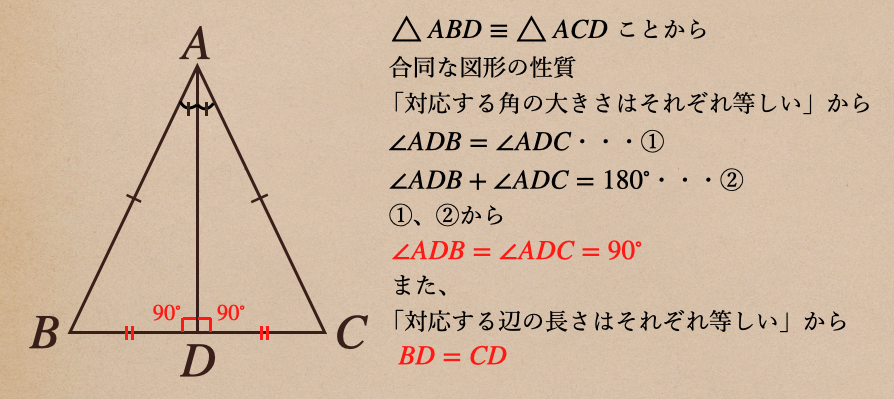
このことから、線分\(AD\)は線分\(BC\)は垂直(\90^\circ\))となっていて
さらには、点\(D\)は線分\(BC\)の中心にあるってことがわかったね。
これも、二等辺三角形の性質になっていて
[二等辺三角形の性質]
定理:二等辺三角形の頂角の二等分線は
底辺を垂直に二等分する
二等辺三角形には、この2つの性質(定理)っていうのがあって
どちらも、これからの数学では、よく使われるものになるので
定理の文言と、どういうことを言っているのかっていうのは、わかっておくように
しておいてください。
今までは、二等辺三角形は定義にもあるように2つの辺が等しいってことだったんだけど
この辺の長さがわかっていなかった時に、どうなるのかっていうのを見てみよう。
ちなみに、2つの辺の長さがわかっていないってことになるので、この三角形は
二等辺三角形かどうかもわからないってことになるんだ。

辺の長さがわかっていない代わりに、\(\angle ABD\)と\(\angle ACD\)が
等しい時、\(\bigtriangleup ABD\)と\(\bigtriangleup ACD\)が合同であることを
証明してみよう。今回の場合の仮定と結論は。。
仮定:\(\angle ABD=\angle ACD\)、\(\angle BAD=\angle CAD\)
結論:\(\bigtriangleup ABD \equiv \bigtriangleup ACD\)
ってことになるね。これから証明していくと。。

この証明で、\(\angle ABD\)と\(\angle ACD\)が等しいと
\(\bigtriangleup ABD\)と\(\bigtriangleup ACD\)が合同ですってこともわかったよね。
合同な図形の性質から、\(AB=AC\)ってこともいうことができるよね
これっていうのは、2つの辺が等しいってことになるので、この\(\bigtriangleup ABC\)は
二等辺三角形ですよってことが言えたってことになるんだね。ようするに。。
[二等辺三角形であるための条件]
定理:2つの角が等しい三角形は二等辺三角形である
これは、2つの辺の長さがわかっていなくても、2つの底角が等しいことが言えれば
その三角形は二等辺三角形ですってことを言うことができるってことなんだね。
ここで出てきら、定義、定理っていうのがどう言ったものなのかっていうのが
わかりにくいよね。
次の項では、その定義、定理、性質について、少し解説を行なっておきますね。
(2)定義、定理、性質について
この定義と定理の違いって何?って人のために、ここでできるだけわかりやすく
解説していきますね。
まずは、定義と性質、定理について、一般的に説明されていることを書くと
定義:ある事柄を同じ意味を持つように用語の意味を簡潔に述べたもの
性質:定義から証明された事柄
定理:性質の中で、特に重要とされているもの
定義にある用語っていうのは、「二等辺三角形」や「正三角形」のことを指していて
その用語を簡単に言っているものが定義ってことになるんだね。
例えば、「2つの辺が等しい三角形は二等辺三角形である」って具合に
2つの辺が等しいってことと、三角形ってことからこの図形は二等辺三角形ですよって
ことを述べているってことになるんだね。逆に言うと、この言い方から
違う形の三角形っていうのはなくて、二等辺三角形以外にありえないってことになるんだね。
定義っていうのは、用語1つに対して、1つの説明しかないってことになるんだね。
数学では、図形の形をこの定義で述べられたりするんだけど、この定義っていうのは
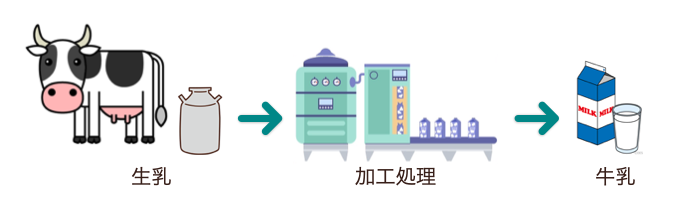
いろいろなところで使われていて例えば「牛乳」の定義は?って言うと
牛乳の定義:生乳を均質化処理して加熱殺菌したもの
って言うのが、牛乳の定義ってことになるんだね。
ちなみに生乳っていうのは牛からしぼっり取ったミルクのことを言うんだね。
こんな風に、いろいろなものに定義っていうの決められているので、用語の定義っていうものに
どんなものがあるのかっていうのを調べてみるのもおもしろいかもね。
次に「性質」は?ってなった時に、上にも書いたように「定義から証明された事柄」ってことに
なっていて、二等辺三角形では、一つ前のところで証明してたように
【二等辺三角形の性質】
2つの底角は等しい
頂角の二等分線は底辺に垂直に二等分する
2つの角が等しい三角形は二等辺三角形である
っていうことになるんだね。
さっきの「牛乳」で見てみると定義は『生乳を均質化処理して加熱殺菌したもの』で
性質はって言うと例えば『牛乳は白い』だったりするね。
確かに牛乳は白いけど、これって証明された事柄なの?って思うかもしれないんだけど
この牛乳が白いのには、ちゃんとした理由があって。。
牛乳の栄養素にに多く含まれる、牛脂肪や牛タンパク質が光に乱反射して白く見える
ってことらしいんだ。こんな風に証明することができて、当たり前の事柄っていうのが
「性質」ってことになるんだね。
じゃあ、「定理」は?っていうと、「性質の中で、特に重要なもの」ってことになるんだけど
これっていうのは、人によって、その性質が重要かどうかっていうのは、変わってくるよね。
なので、この「定理」っていうのは『性質=定理』って考えてしまってもいいかなって思うんだね。
ただ、数学では、教科書なんかで、性質の中から定理として説明されているものもあるので
そこは、しっかり区別しておこう。
ちなみに、二等辺三角形の定理っていうのは。。
【二等辺三角形の性質】
定理:二等辺三角形の2つの底角は等しい
定理:二等辺三角形の頂角の二等分線は底辺に垂直に二等分する
定理:2つの角が等しい三角形は二等辺三角形である
ってことになるね。
(3)逆・反例
この逆(ぎゃく)っていうのは仮定と結論を入れ替えることを言うんだね。
仮定と結論が入れ替わっている2つのことがらの
片方をもう一方の 逆(ぎゃく) という
例えば、「\(x=3\)ならば\(x+4=7\)である」の
逆は「\(x+4=7\)ならば\(x=3\)である」ってことになるんだね。
これは、逆の場合でも成り立っていることが言えるよね。
けど、「\(x=3\)、\(y=4\)ならば\(x+y=7\)である」の
逆は「\(x+y=7\)ならば\(x=3\)、\(y=4\)である」の場合
この逆のことがらっていうのは、「\(x=1\)、\(y=6\)」でも成り立つよね。
こんな風に仮定を満たしているけど、結論を満たしていない例を
反例(はんれい)って言って、逆が成り立っていない時っていうのは
この反例を一つ挙げて成り立っていませんよってことを証明してあげればいいってことになるんだ
(4)正三角形
今度は、正三角形について見てみるね。
正三角形って言うと、3つの辺が等しい三角形のことだよね。
このことも定義とされていて
正三角形の定義:3つの辺が等しい三角形を正三角形と言う
そのまんまだね。
正三角形って言うのは、3つの辺が等しいんだけど
言ってしまうと2つの辺が等しいとも言えるよね。
2つの辺が等しい三角形っていうと、二等辺三角形だったよね。
ようするに、正三角形は二等辺三角形の特別なものってことになるんだね。
二等辺三角形の定理を当てはめて、正三角形って言うのはこんなことが証明できるんだ。。

この証明によって、正三角形の3つの角は等しいってことが言えたんですね。
これが正三角形の性質になって
【正三角形の性質】
定理:正三角形の3つの角は等しい
正三角形は3つの辺が等しい、3つの角が等しいって言うのは、小学生でも
習ってきて、当たり前って思うかもしれなんだけど、この数学では
どう言ったものが正三角形かって言う定義をはっきりさせたり
証明を用いて、3つの角が等しいことを言っていて
本当にそれが正しいことを明確にしてあげたってことになるんですね。
なので、今後は数学での正三角形の言い方として定義と定理っていうのは
覚えておきましょう。
(5)直角三角形の合同条件
直角三角形は1つの角が90°の三角形のことでしたよね。
なので、直角三角形の定義はって言うと。。
正三角形の定義:1つの角が直角(90°)の三角形を直角三角形と言う
この直角三角形は1つの角が直角ってことが決まっている三角形ってことになるので
三角形の合同条件とはまた違った合同条件っていうのがあるのでそれを証明しながら
確認していきますね。
ちなみに、三角形の合同条件っていうのは。。
【三角形の合同条件】
1.3つの辺がそれぞれ等しい
2.2つの辺とその間の角がそれぞれ等しい
3.1つの辺とその両端の角がそれぞれ等しい
ってことだったよね。
2つの直角三角形を見たときに、どう言った条件で合同ってことが
言えるのかっていうのを見ていきますね。
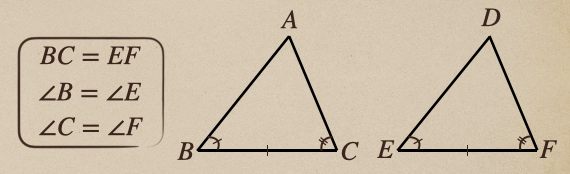
まずは、2つの直角三角形で次の場合

この条件のときで見たとき、\(\bigtriangleup ABC\)と\(\bigtriangleup DEF\)の
\(AC\)と\(DF\)を一つの辺として重ね合わせると。。

こんな風にしてみることができますよね。
ここで、\(\bigtriangleup ABE\)を見たとき、\(AB=AE\)で2つの辺が等しい三角形になってるよね
ってことはこの\(\bigtriangleup ABE\)は二等辺三角形ってことが言えますよね。
そうすると、二等辺三角形の定理の証明で行ったように
\(\bigtriangleup ABC\equiv \bigtriangleup AEC\)ってことが言えて
すなわち、\(\bigtriangleup ABC\equiv \bigtriangleup DEF\)となるね。

もう一つ、見ていこう。

この場合も、さっきと同様に合わせることで二等辺三角形としてみることが出来て
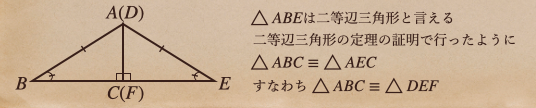
これも、\(\bigtriangleup ABC\equiv \bigtriangleup DEF\)ってことを言うことができるんだね。
ここで、直角三角形にも、辺と角に呼び方があって
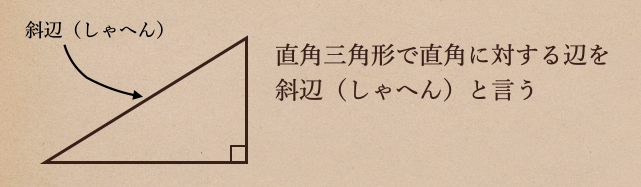
それと、角っていうのも
\(0^\circ\)より大きく、\(90^\circ\)より小さい角を鋭角(えいかく)と言う
\(90^\circ\)より大きく、\(180^\circ\)より小さい角を鈍角(どんかく)と言う
角の大きさによって、呼び方が違っていて、これは、図形の角で共通の呼び方になるので
覚えておこう。
そして、直角三角形の合同であるための条件っていうのをまとめると
【直角三角形の合同条件】
定理:2つの直角三角形は次のどちらかが成り立つとき合同である
(1)斜辺と他の1辺がそれぞれ等しい
(2)斜辺と1鋭角がそれぞれ等しい
普通の三角形の合同条件とは違った条件で、合同であることが言えるってことなんだね。
これも定理となっているので、しっかり理解しておいてください。
今回は、ここまでになります。
ここまでの記事が良かったと思ったらここをクリックしてね。
質問なんかがあった場合はコメントにお願いします。
では、またさようなら






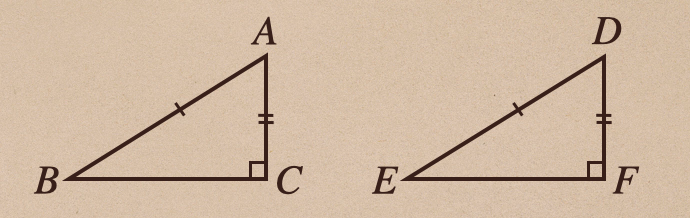
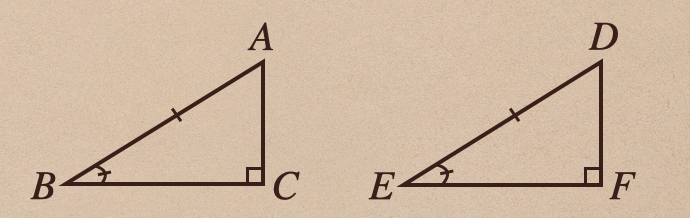


コメント