どうも、こんにちはDKです。
今回は「平方根」について解説を行っていきますね。
今までの中学数学は学年ごとに習った単元(中1:平面図形、中2:平行と合同)のように
中学1年生で習った単元の応用を中学2年生で習うみたいなものが多かったんだけど
この平方根に関しては、中学3年生で初めて登場するものになるんだね。
なので、ここで基礎をしっかり学んで、しっかり理解していってください。
では、基礎の解説始めていきますね。
1.平方根の表し方
ここに、面積が\(1cm^2\)の正方形があったとして
これって言うのは、1辺の長さが\(1cm\)ってことになるよね。
面積が\(4cm^2\)の正方形であれば、1辺の長さは\(2cm\)ってことだよね。

これは、四角形の面積である「底辺×高さ」から導き出しているんだよね。
じゃあ、面積が\(2cm^2\)の正方形の1辺の長さを求めたいってなったとき
求めることができるかな?

実際にこれを求めていくってなると、\(2cm^2\)の1辺の長さは
\(1.41421356237\)…と延々と続いていくような値になるんだね。
こんな値を毎回、書き表すことも大変なんで、こういった値となるものには
記号\(\sqrt{a}\)を使って、\(\sqrt{2}\)として表すことにしているんだね。
これを『ルート2』って読み方をするんだね。
\(a≧0\)のとき「2乗して\(a\)となる数」
\(x^2=a\)を成り立たせる\(x\)の値を\(a\)の平方根(へいほうこん)と言う
ってことなんだね。
なので、\(2cm^2\)の正方形っていうのは、1辺が\(\sqrt{2}\)と表されて

\(\sqrt{2}×\sqrt{2}=2\) ➡︎ \((\sqrt{2})^2=2\)
となるってことなんだね。平方根って言うのは。。。

ってことで、まとめると…
【平方根】
1.正の数の平方根は2つある
それらの絶対数は等しく、符号は異なる
2.0の平方根は、0である
正の数\(a\)の平方根を記号(ルート)を使って正:\(sqrt{a}\)、負:\(-sqrt{a}\)と
表すことができるんだけど、この記号(ルート)を根号(こんごう)と呼ぶんだね。
そして、これは平方根の定義として次のことが言えるんだね。

このaっていうのは正の数になるよ。
この平方根の定義からこんなことも言えるんだね。

ほかにも、根号を使って表した数の中には根号を使わずに表すことがきるものもあって
それが、\(4\)、\(9\)、\(25\)のように整数を2乗したときの数っていうのは
平方根で表すと\(\sqrt{4}\)、\(\sqrt{9}\)、\(\sqrt{25}\)となるんだけど
これらは、\(\sqrt{4}=2\)、\(\sqrt{9}=3\)、\(\sqrt{25}=5\)として
根号を使わずに表すことができるんだね。
こんな風に整数を2乗したときの数の平方根っていうのは
整数として表してあげることができるってことを覚えておこう。
2.平方根の大小
次に平方根の大きさについて考えていこう。
1章でも出てきた正方形で次の場合についてみていくと

2つの正方形があって、それぞれの面積を\(2cm^2\)と\(5cm^2\)だった場合
その、正方形の1辺の長さはそれぞれ、\(\sqrt{2}cm\)と\(\sqrt{5}cm\)ってことになるよね。
この2つの平方根で大きいのはどっちかっていうと、図からもみて分かる通り
\(\sqrt{2}<\sqrt{5}\)ってことになるんだね。実際にこの2つの平方根を根号をなくして
表してあげると。。
\(\sqrt{2}=1.4142135623\)
\(\sqrt{5}=2.2360679775\)
となるんだね。これからみても、\(\sqrt{5}\)の方が大きいよね。
ようするに、平方根の大きさっていうのは
【平方根の大小】
\(a>0\)、\(b>0\)で \(a<b\)ならば\(\sqrt{a}<\sqrt{b}\)
ってことが言えるってことになるんだね。
これをふまえて、今度は「根号を使わない数と根号の大小」について
考えてみよう。
ここに根号と整数[\(2\)、\(4\)、\(\sqrt{5}\)、\(sqrt{15}\)]があって
これらを小さい順に並べていくとすると。
こういった場合はまず、すべての整数を根号を使った数で表してあげるといいんだね。
ようするに。。。

として表すことができて、すべての数に根号を当てはめて大きさをみていって
あげればいいってことなんだね。
すべて根号の形で大きさをみてみると

となるんだね。これを根号をなくせるものをなくして表すと

これが、[\(2\)、\(4\)、\(\sqrt{5}\)、\(sqrt{15}\)]の大小ってことになるんだね。
だから、整数と根号でどっちの数が大きいのかわからないなぁってなった時は
すべてを根号の形にして、その中の数の大きさで大小を判断してあげよう。
ちなみに金剛に負の符号がついた場合も、整数のときと同じ大きさの関係になるよ。

3.近似値と有効数字
この近似値、有効数字っていうのは、前は中学1年生で習っていた内容になるんだ。
僕のブログの「中1-7.データの活用」と同じ内容になっちゃうけど、ここでも
解説しておくね。
まずは、下の図の線分ABの長さって何mmになるかな?

40mm ? いや、39mmかな?もう少し細かく見てみよう。
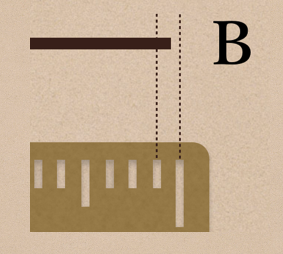
実際は39mm より長くて、40mm よりは短い長さってことだね
この線分ABを\frac{1}{10}まで読み取って 39.7mm って表すこともあるよね
ただ、測定っていうのはどんだけ精密に測ったとしても真の値と
等しくなっているのかっていうのはわからないんだね。
こんな風に測定した値みたいに真の値に近い値のことを「近似値」っていうんだね。
円周率の3.14って言うのも近似値になるよ。
そして、近似値から真の値を引いた差を誤差って言うんだね。
誤差 = 近似値 – 真の値
で計算することができるよ。
さっきの線分ABの長さの近似値40mmっていうのはcmで表すと
4cmってなるよね。これをmmの位までを意味のある数字するために
4.0cmと表すことがあるんだね。
近似値を表す数で、意味のある数字を「有効数字」って言って
その数字の個数を、有効数字の「けた数」って言うんだね。
有効数字の表し方っていうのがあって、これが
測定値で 500 m があったとき「位」取りするために0と有効数字を区別するんだね。
どういうことかと言うと
・1の位まで測定した値のとき、有効数字は 5 , 0 , 0 の3ケタとなる
この場合、 \(5.00×10^2m\) と表される
・10の位まで測定した値のとき、有効数字は5, 0 の2ケタとなる
この場合、\(5.0×10^2m\)と表される
ってことなんだね。どの位までを有効としてあげるのかって言うのをみて
それを値として表してあげてるってことなんだね。
4.有理数と無理数
ここからは少し、言葉を覚えてもらう必要があって、それって言うのが
タイトルにもあった、「有理数(ゆうりすう)」と「無理数(むりすう)」になるんだ。
それぞれがどういったものかって言うと
【有理数(ゆうりすう)】
分数で表すことのできる数
(整数 \(a\)と 0 でない整数 \(b\) を使って \(\frac{a}{b}の形で
表すことができる数)
【無理数(むりすう)】
分数で表すことができない数
それぞれ例をあげると。。

\(\sqrt2\)や\(\pi\)は数字で表すと
\(\sqrt2=1.41421…\)
\(\pi=3.141592…\)
となって、数がずっと続いてしまうことになるので、分数で表すことができない
「無理数」ってことになるんだね。
①\(\frac{3}{8}\)と②\(\frac{1}{7}\)と③\(\frac{1}{11}\)とを小数で表してみると
① \(\frac{3}{8}=0.375\)
② \(\frac{1}{7}=0.142857…\)
③ \(\frac{1}{11}=0.0909090…\)
となって、それぞれ特徴的な値となるんだけど、これらを
①のように小数で終わりのあるものを「有限小数(ゆうげんしょうすう)」
②のように小数で終わりがないものを「無限小数(むげんしょうすう)」
③のようにいくつかの数字が同じ順序でくり返されるものを「循環小数(じゅんかんしょうすう)」
って言うんだね。
この有限小数、無限小数、循環小数にはそれぞれ関係があって
有理数を整数以外の小数で表してものは、「有限小数」か「循環小数」となって
無理数を小数で表すと、循環しない「無限小数」になるんだね。
これらをまとめるとこう言うことだね。

ここでは、言葉とそれがどういったものかって言うのを理解してもらえれば
オッケーかな。
今回は、ここまでになります。
ここまでの記事が良かったと思ったらここをクリックしてね。
質問なんかがあった場合はコメントにお願いします。
では、またさようなら。



コメント