どうも、こんにちはDKです。
今回は関数の基礎についてやっていこう。
動画でも方程式の基礎を公開しているのでこちらも見てみてください。
※音が出るので、周りに気をつけて再生してみてね。
この関数では、方程式で使っていた \(x\) の他に \(y\) を使った
等式(イコールで結ばれた式)が出てくるんだ。
方程式の部分でまだ、わからないがあるようなら ここ から
方程式の基礎をもう一度、復習してみよう。
では、関数についてやっていくね。
関数
例えば、こんな場合を考えてみよう。
周の長さが30cm の四角形があったとするよね。
この四角形の横の長さが
①6cm の場合、②8cm の場合、③10cm の場合
だったとき縦の長さはどうなるかな?
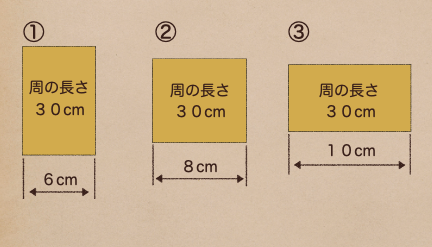
①から③は全て周の長さが30cmになるってことだったよね。
だからこの場合、(横+縦)×2=30ってことになるよね。
だから、縦の長さは「15 – 横の長さ」で決まるよね。
ここで、横の長さを \(x\) 、縦の長さを \(y\) とした場合
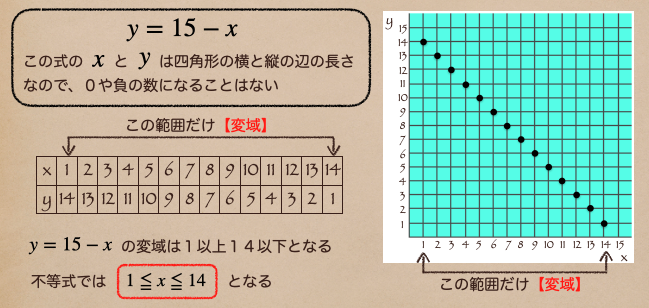
\(y=15-x\) って式で書くことができるよね。
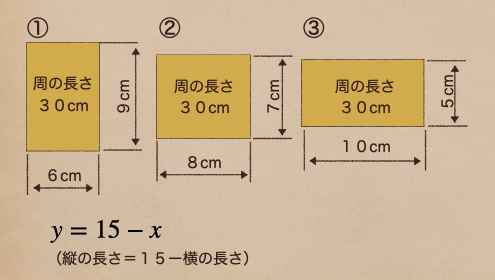
じゃあ、横の長さ \(x\) の数が変わっていくと、縦の長さを \(y\) は
どのように変わっていくのか見てみよう。
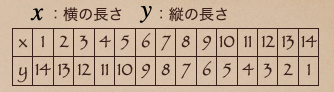
横の長さ \(x\) の数が1の時は縦の長さ \(y\) は14となって
\(x\) が大きくなると \(y\) は小さくなっていってるね。
こんな風に \(x\) や \(y\) みたいにいろいろな値をとる文字を変数って言うんだね。
\(x\) の値を決めるとそれに対応して \(y\) がただ一つ決まるとき
\(y\) は\(x\) の関数である って言うんだね。
表やグラフで関数をあらわす
今度は先ほどやった \(y=15-x\) で \(x\) の値が変わっていくとき
対応する \(y\) の値が変わるようすを表やグラフであらわしてみよう。
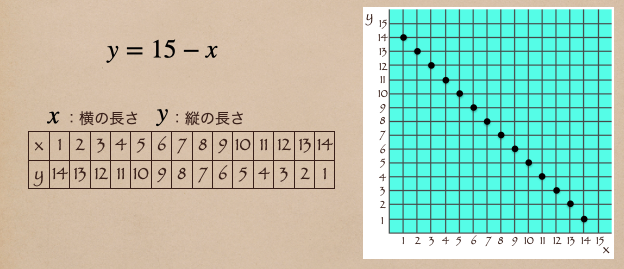
さっきも言ったように \(x\) の値が大きくなると、 \(y\) の値は小さくなっていたよね。
\(x\) と \(y\) をグラフで書く場合は横軸を \(x\) 、縦軸を \(y\) で書くようにするんだよ。
横軸( \(x\) ) は右に行くほど大きくなって
縦軸 ( \(y\) ) は上に行くほど大きくなるように書くんだよ。
グラフは \(x\) が1の時に \(y\) は14、 \(x\) が2の時に \(y\) は13に
点をつけていったら上の右の図のような形になるよ。
また、今回の \(y=15-x\) は四角形の周の長さ30cmから横と縦の長さを求めることだったよね。
このような場合 \(x\) の値は決められた数字しか入れられないよね。
ようするに範囲が決まっているってことなんだけど
この変数の値をとる範囲のことを変域(へんいき)って言うよ。
こんな風に関数には変域があるものなのか、そうでないのかって言うのも
初めのうちはわからないかもしれないけど、問題なんかを解いているときに
その問題には成り立たない状態があるのかを考えてみるといいよ。
例えば、三角形や四角形は分かりやすいよね。
三角形の場合は3つの辺が存在しないと三角形とは言わないし
四角形も4つの辺がないといけないから、その範囲でしか成り立たないってことになるよね。
そうやって、状態が成り立つかどうかを考えられる力も身につけていってね。
じゃあ、次は比例についてやっていこう。
比例
ここでも、一つ例を見て考えていこう。
まず、毎分3Lでビーカーに水を入れたとするね。
その場合、 \(x\) 分後にビーカーに入った水の量を \(y\) とした時
どんな等式がつくれるかな?
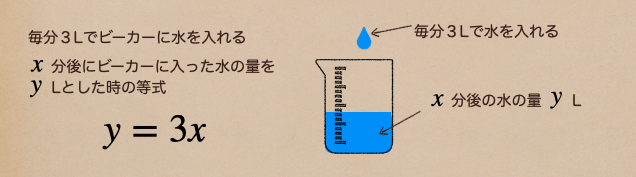
1分で3L入るってことになるから、\(x\) 分 × 3L = \(y\) だね。
だから、等式は \(y=3x\) になるよね。
ここで、この3っていうのが、定数って呼ばれるもので字の通り「定められた数」て
ことで、決められた変わることのない数のこと言うんだね。
\(y=3x\) っていうのは\(x\) が1上がれば、 \(y\) は3上がるよね。
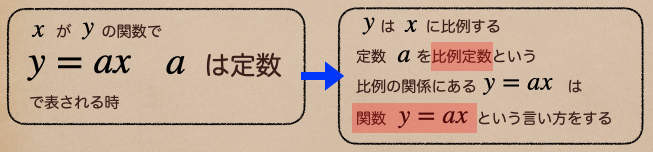
このような関係を \(y\) は \(x\) に比例するって言うんだ。また、
この定数3って言うのは、比例定数っていう言い方をすることもできるんだね。
ここまではいいかな?
ようするに、\(y\) は比例定数3の倍数で表されるってこと。
比例の関係 \(y=ax\) はこんな特徴もあるよ。

上の図は関数 \(y=3x\) の表になるんだけど、\(x=1\) から \(x=3\) になった時って
3倍になってるよね?この時、\(y\) も3倍になっているのがわかるかな?
他にも、\(x\) が5倍になったら、\(y\) も5倍になってるよね?
\(x=3\) から3倍になった時も、その解である\(y=9\) も3倍になるんだね。
こんな風に比例の関係にある関数っていうのは
\(x\) が2倍、3倍すると \(y\) も2倍、3倍するんだ。
また、比例定数 a は\(\frac{y}{x}\) であらわすことができるんだ。
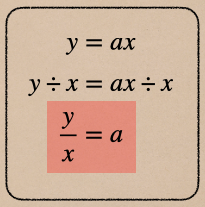
比例の関係 \(y=ax\) は負の値を取るこもあるんだ。
どういうことかをさっきのビーカーに水を入れる場合を例に考えてみよう
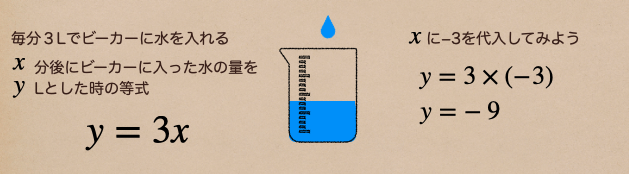
毎分3Lで水を入れているってことだから、関数 \(y=3x\) ってなるよね。
じゃあ、ここに \(x=-3\) を代入してみた場合、右側の式の通り \(y=-9\) になるよね。
じゃあ、 \(x=-3\) や \(y=-9\) はどういうことを言っているのか
−3分? −9Lってことになるんだけど、こんな時はこんな風に考えてみよう。

ある程度、水が入った状態のビーカーを基準(0分)としてみた時に
そこから、時間がすぎて \(x\) 分後は水の量が増えるよね。
じゃあ、−3分後は?っていうと、ビーカーに入っている水の量が少なくなる方向になるよね。
なので、ここでの言い方は3分前には水は9L少なかったってことになるんだね。
注意しないといけないのは、ビーカーの水が0Lだった場合は、3分前でもちろん水は0Lだよね。
間違っても、−9Lってしないようにね。
ある程度、水が入っているから、−3分後、−9Lが成り立つんだよ。
ここまでが、比例についてになるよ。
関数、比例についてはわかったかな?
まだ、?がついているようなら、もう一度、おさらいしてみてね。
ここで挙げている例以外に対しても考え方は一緒だから、違う例題や問題を
解いてみて、ここでの復習にしてみるのも、ありだね。
反比例
次は反比例(はんぴれい)についてやっていくよ。
反比例って聞いて「反」って言うくらいだから、比例の反対って言うのはなんとなく想像つくよね。
けど、比例の反対ってどう言うことかいまいちわからないよね。
じゃあ、とりあえず次のような場合を考えてみよう。
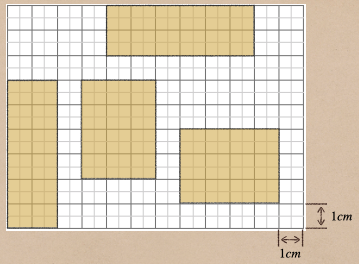
図のマス目に四角形を作ってみるよ。その四角形は面積が \(12cm^2\) になるようにしよう。
上の図のように色々な四角形ができるよね?
じゃあ、横の長さを \(x cm\)、縦の長さを \(y cm\) としたときにどんな関係の式ができるかな
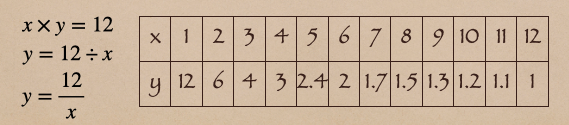
四角形の面積は横×縦だったよね。
だから、横(\(x\))×縦(\(y\))が面積でその面積が\(12cm^2\)となるってことだよね。
それが上の左側の式になるんだ。これを\(y=\)の形にしていくと…
\(y=\frac{12}{x}\)になるんだね。ちなみにこの関数の\(x\)と\(y\)の値を表にすると
上の右側になるんだ。
表を見てみると12を\(x\)の値で割って言ってるよね?
これは関数\(y=\frac{12}{x}\)を見てもわかるね。
ここまでくればわかるかな?そうだね、この関数\(y=\frac{12}{x}\)が反比例って言うんだね。
ちなみに、こう言うこと
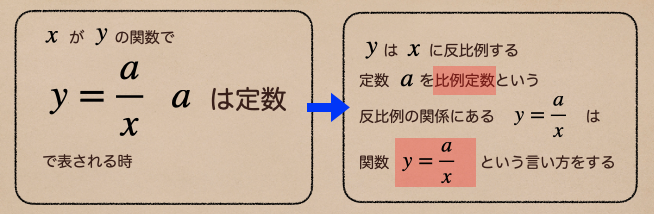
\(y=\frac{a}{x}\)のことを反比例するって言うんだね。
ちなみに、ここのaは比例定数って言うんだよ。この言い方は比例の時と一緒だね。
\(y=\frac{a}{x}\)の式を、反比例の関係もしくは関数っていう言い方をするよ。
関数は比例、反比例両方の場合で使えるってことだね。
反比例にはこんな特徴もあるよ。
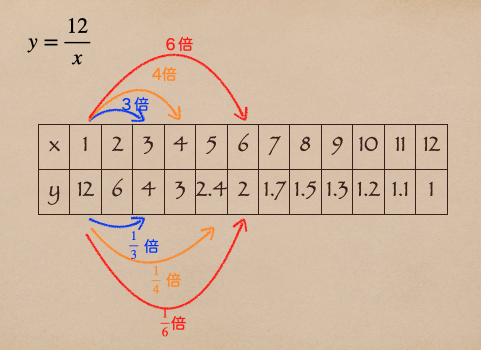
\(x\)の値が3倍、4倍、6倍となった場合
\(y\)は\(\frac{1}{3}\)倍、\(\frac{1}{4}\)倍、\(\frac{1}{6}\)倍になるってことだね。
ここまでは、変数(\(x\)、\(y\))が正の数の時を表にしてあらわしてきたけど
今度は、負の数まで見た時にどのようになっていくかを見ていこう。

反比例の関係の\(x\)と\(y\)の値でも、同じように符号が変わっていくんだ。
ただ、ここで注意しておかないといけないのは、\(x\)の値が0の時だね、
このときは\(y\)の値はないってことだね。
これは、分数で分母に0が来ることはないからってことだね。
なので、表の\(x=0\)の時、\(y\)は「x(ばつ)」にしてるんだ。
反比例についてわかったかな?この比例、反比例ってところは苦手って人も
多いと思うから、こういうものとして覚えるのではなく、なぜそうなのかをしっかり学んで
次に行こう。
今回のブログはここまで。
次回は、座標、比例のグラフ、反比例のグラフをやっていくね。
では、最後までみてくれてありがとうございました。





コメント