どうも、こんにちはDKです。
今回は前回の関数(1)の続きをやっていくね。
ここでは、グラフの見方、書き方がメインとなってくるので
関数、変数、定数や比例・反比例ってなに?ってなっているようなら、ここ から
関数(1)を見てみてね。しっかり理解してから、次に進もう。
動画でも方程式の基礎を公開しているのでこちらも見てみてください。
※音が出るので、周りに気をつけて再生してみてね。
座標
では、初めに座標について学んでいこう。
グラフを書く上で、座標って何?っていうのがわかっていないと
グラフを書くことに苦労してしまうから、しっかり理解していこう。

上の図のように男の子と女の子が整列していたとするね。
この時、四角で囲った男の子はどこにいるかって言うのを知らせるときって
どうやって知らせてるかな?
きれいに整列しているんだから、横列と縦列に番号をつけて横列と縦列を特定することで
彼の位置を知らせるよね。
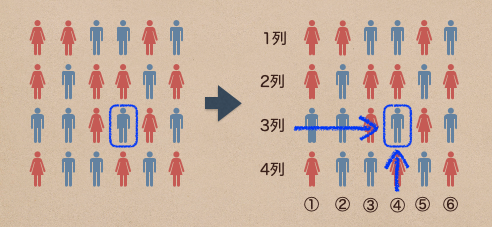
縦列を1列〜4列として、横列を①〜⑥で番号を入れてあげると
青枠の男の子の位置は特定できるよね。この場合、3列の④だね。
こうやって、平面としてみた時に位置を表すことができるね。
これを、図にしてみると…
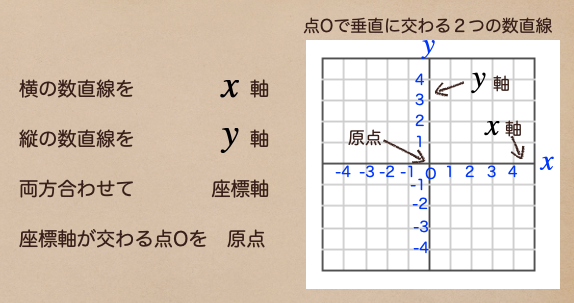
こんな風に、\(x\) の数直線と \(y\) の数直線を使って図を作ることができるんだね。
それぞれの呼び方は 横線を \(x\) 軸、縦線を \(y\) 軸、両方合わせて座標軸
っていう言い方をするんだ。座標軸の交わる点O(オー)を原点って言うよ。
この原点Oは2つの数直線の0(ゼロ)を表す点のことを指すからね。
今度はこの座標軸に点を置いてみよう。

\(x=2\)、\(y=3\)の場合、右側にある座標軸に
\(x\)軸側に 2 行って、 \(y\)軸側に 3 行ったところ(図で見ると黒い点のところだね)
ここの黒い点を点 A としておくことができるんだね。
この点 A を A ( 2 , 3 ) と表すことができるんだ。
この A ( 2 , 3 ) を座標っていう言い方をするよ。
また、2 を\(x\)座標、3を\(y\)座標っていう言い方をすることも覚えておこう。
じゃあ、もう少し座標を図に書くことをしていくね。
ここの座標を図にかき入れていくことは多少、慣れが必要になるから
いろいろな問題を繰り返し行なっていこうね。
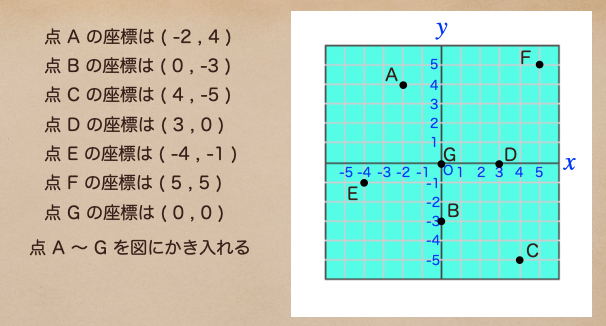
点 A 〜 点 G の座標をそれぞれ、図にかき入れたらこんな風になるね。
図へのかき入れる上で、注意してしないといけないのが
\(x\)軸は横線だからプラスになれば右に進むし、マイナスであれば左に進むよ。
\(y\)軸は縦線だから、プラスになれば上に行って、マイナスになれば下に行くってことだね。
よく、\(x\)軸、\(y\)軸をまちがえてしまって、\(x\)座標の数を縦側にしてしまうなんてことも
あるから、気をつけようね。
図にかき入れる場合は
①横(\(x\)軸)方向 ②縦(\(y\)軸)方向の順に数をしっかり進めるようにして
座標の点をかき入れよう。
点Aの場合は \(x=-2\) 、\(y=4\) だから、①左に2つ行って、そこから②上に4つ上がったところが
点Aになるってことだね。
点Bの場合は \(x=0\) 、\(y=-3\) だから、①\(x\)軸方向は0だから原点O(オー)だね。
② \(y\)軸方向は下方向に3行ったところが点Bになるね。
他の点も、①\(x\)軸方向、②\(y\)軸方向にそれぞれ、移動して行ったところに点が来るかを
確認してみてね。
次は比例のグラフについてやっていくね。比例のグラフからのここでやった座標の
点を正確にかき入れていく必要があるから、座標、図へのかき入れがまだ自信ないって場合は
もう一度、見直したり、色々な問題をやってみよう。
比例のグラフ
比例のグラフってのは小学生でも習ってきたと思うんだけど、正の数の変域(0以上)の場合だけ
だったと思うんだ。中学校からは負の数側まで考えてグラフを書いていく必要があるんだね。
比例の関係\(y=2x\)で考えてみよう。
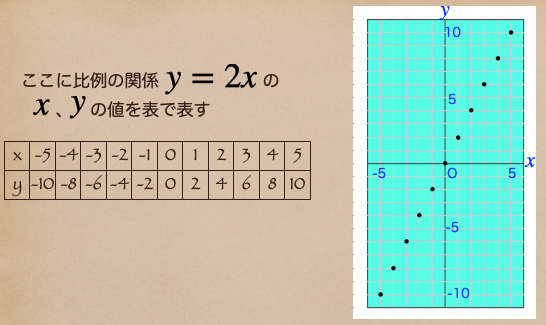
\(y=2x\)の\(x\)と\(y\)の値を求めると左の表のようになるよね。
この\(x\)と\(y\)の値の組みをそれぞれ、点を図に書き入れいると右のようになるね。
ここからさらに、細かい\(x\)と\(y\)の値の組みを書き入れていったらどうなるかな?
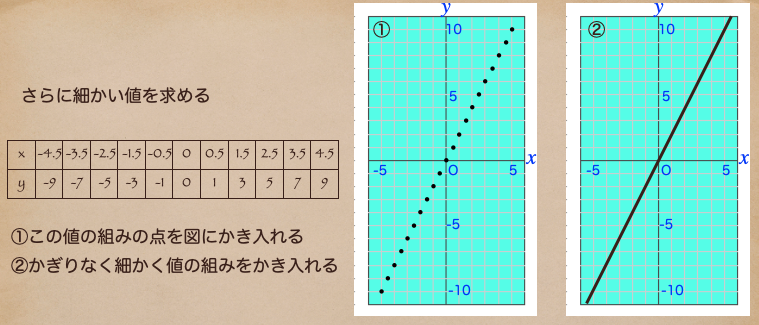
さっきの\(x\)の値を間の0、0.5、1.5…として\(y\)の値を求めて表にしてるよ。
この\(x\)と\(y\)の値の組みを図にかき入れたのが①になるよ。
ここから、さらにかぎりなく\(x\)と\(y\)の値の組みを図にかき入れていくと
どうなるか… そうだね、点だったものが一つにつながって直線になってくるんだね。
この直線を比例の関係\(y=2x\)のグラフっていう言い方をするんだ。
今度は、\(y=-2x\)について見てみよう。さっきの比例の関係\(y=2x\)の符号が変わった状態だね。

同じようにまずは\(x\)と\(y\)の値を表にしてから、\(x\)と\(y\)の値の組みを図に
かき入れていくよ。その図が①になるよ。
そこから、さらに細かく\(x\)と\(y\)の値の組みをかき入れていったら
図②のような直線になるね。これが\(y=-2x\)のグラフになるんだね。
ここで、\(y=2x\)と\(y=-2x\)のグラフを見比べて何か気づくことない?
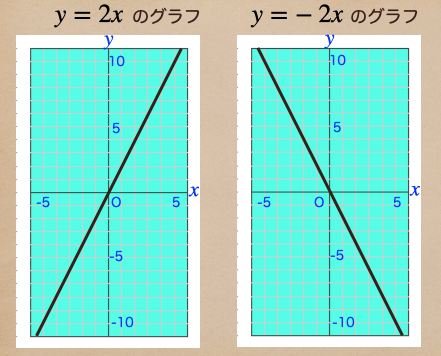
こうやって\(y=2x\)のグラフと\(y=-2x\)のグラフを並べて見るとわかってくるかな。
そうなんだ、2つのグラフは\(y\)軸を中心に左右対称になってるんだね。
他にもこんなことが言えるんだ。それは…
\(y=ax\)は原点を通るグラフである
\(y=ax\)の定数aが正の数の時、グラフは右上がりとなる
\(y=ax\)の定数aが負の数の時、グラフは右下がりとなる
ってことなんだ。図にかいて見てみよう。
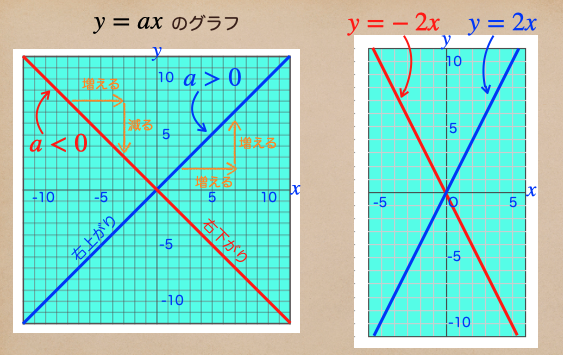
\(y=ax\)のグラフがあるとするよ。
a > 0 は a が正の数だよね。この時のグラフは青線で引いた直線になって
a < 0 は a が負の数だよね。この時のグラフは赤線で引いた直線になるんだね。
青線の a > 0 は右上がりの直線で\(x\) が増えると、\(y\)も増えるんだ。
逆に赤線の a < 0 は右下がりの直線で\(x\) が増えると、\(y\)も減るんだね。
だから、さっきの\(y=2x\)は右上がり、\(y=-2x\)は右下がりになるんだね。
これは、どんな数に対しても言えることだから、ここを覚えておけば
グラフを書いた時に a が正の数なのに右下がりのグラフを書いていたりした場合は
おかしいって気づくこともできるよ。
比例には変域ってのがあったよね?
変域をグラフに書く場合どうなるのか考えてみよう。
家から図書館まで15kmの道のりを自転車で毎時5kmの速さで進むとする。
自転車で進んだ時間を \(x\)、その時に進んだ道のりを \(y\)として
それを関数で書くと… \(y=5x\) ってなるよね。これをグラフに書くと…
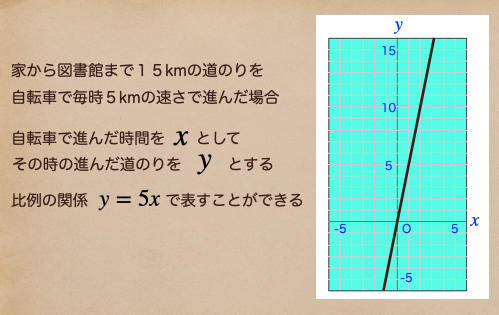
こんなグラフになるよね、\(x\)が1進むと\(y\)は5上がるんだね。
ただ、ここで注意しないといけないのが今回は15kmの道のりっていう条件がついているよね。
ってことは、道のりの最大は15kmってことになるよね。
また、道のりは家からスタートしていて図書館に向かうだけなので、図書館の反対側に
進む(マイナス方向にいく)ことも考えなくていいね。
だから、この例題の道のりは0km〜15kmの範囲ってことになるので
変域が\(0\leqq y \leqq15\)ってことになるね。じゃあ、\(x\)は?ってなった時
\(y=0\)と\(y=15\)で解いてあげれば\(x\)の変域もわかるよね。
なので、\(x\)の変域は \(0\leqq x \leqq3\)ってことになるね。
じゃあ、この変域をグラフに書き込んでいこう。
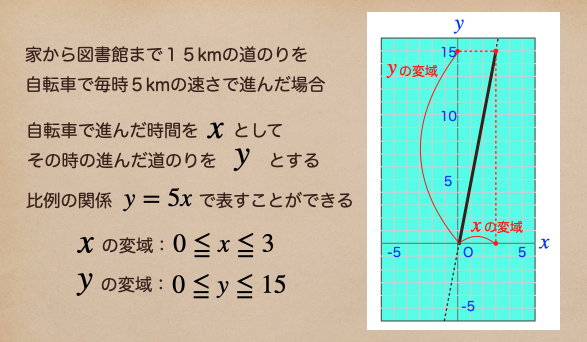
変域がある比例の関係をグラフに書くときは、変域の範囲内を実線で書いて、
変域の範囲外は点線で書くようにしよう。
ここでは、比例の関係式の\(x\)と\(y\)の値の組みをいっぱい書いて直線にするっていう説明を
したけど、実際には比例の関係\(y=ax\)の場合は一組みの\(x\)と\(y\)の値の組みを
図に書き出して原点と直線で結んであげれば、グラフはできるからね。
確認作業として、別の点の値の組みを図に書き込んだ時に、そのグラフ上にくるかどうかを
見てあげれば、正しいグラフが引けているかはわかるからね。一度やって見て。
ここまでが比例のグラフになるよ。図ばかりで疲れちゃったかな?
このグラフを書くって言うのも、慣れるまで書き方を間違えてしまいがちなんで
しっかり理解して、理解したら問題を解いて正しいグラフが引けるようになるまで
繰り返しやっていこう。
反比例のグラフ
ここからは、反比例のグラフについてやっていくね。
比例のグラフは、まっすぐな直線だったよね。反比例はどんなグラフになるのかな?
まずは、反比例の関係\(y=\frac{6}{x} \)を見てみよう。
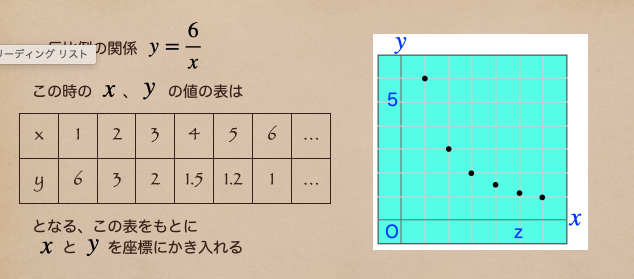
反比例の関数を座標にかき込むと右図のようになるんだね。
じゃあ、比例のグラフでもやったようにもっと細かく、点を書き込んでみよう。
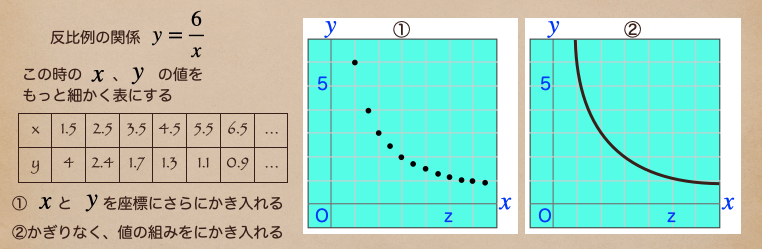
かぎりなく\(x\)と\(y\)の値の組みをかき入れていくと②のように線になったね。
今度の線は、直線じゃなく曲線になっていることがわかるよね。
これが反比例の関係\(y=\frac{6}{x}\)のグラフになるんだね。
この反比例の関係\(y=\frac{6}{x}\)で\(x\)が100、1000、10000となった時
\(y\)の値は0.06、0.006、0.0006ってなるよね。
また、逆に\(x\)が0.01、0.001、0.0001となるときに
\(y\)の値は600、6000、60000ってなるよね。
これって、どういうことかわかるかな?
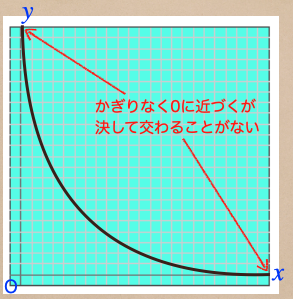
反比例の関係式の場合、0を通らないってことだね。
さっきの反比例のグラフの曲線は0に近づいていくんだけど、決して0と交わることがないんだね。
これが反比例の特徴になるんだ。
今度はさっきの反比例の関係 \(y=\frac{6}{x}\) \(x\)の値に負の値も含んで考えてみよう。
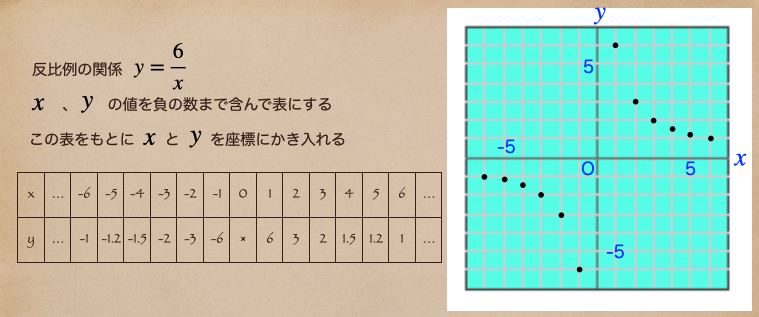
\(x=0\)のときはさっきも行ったように反比例のときは\(y\)の値はないだったよね。
この表を図にかき込むと右の図のようになるよね。
これを実線で書き表すと…
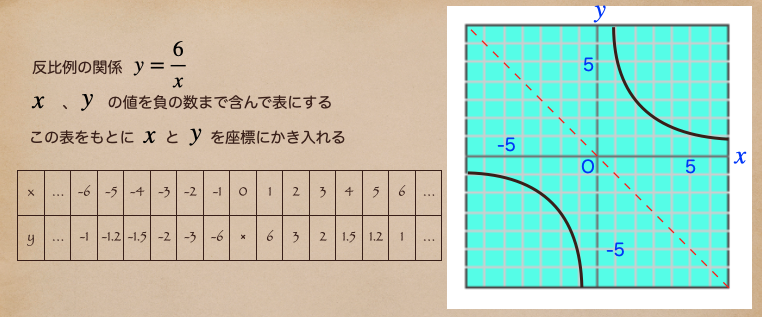
反比例のグラフは\(x\)が正の数と負の数が一本の線でつながっていないってことなんだね。
特徴としては赤い点線で引いた線に対称にグラフができているってことだね。
反比例の線は曲線になっている上に、比例の時のように均等になっているわけではないから
グラフを書くときは少し、苦労する(上手に書けない)と思うんだけど
反比例のグラフも、比例のグラフも\(x\)、\(y\)の値の組みが正しく図に書きこめて
その点にグラフの線が来ていれば多少、線がゆがんでいても○はもらえると思うよ。
ようするに、関数を表にして\(x\)、\(y\)の値の組みを理解している、
その\(x\)、\(y\)の値の組みを図に書き込めむことができれば、
ここのグラフを書くことは理解できているって言えるからね。
でも、できる限り、定規やコンパスを使ってきれいに線を引くようにしていく方がいいね。
反比例の関係をもう少し、やっていくよ。
次は、定数 a が正の数、負の数のときどうなるか見ていこう。
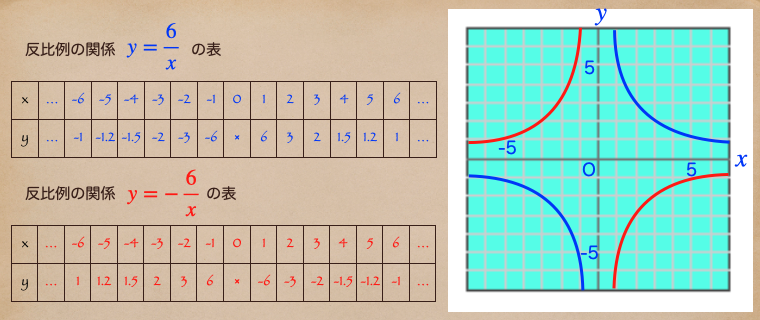
定数 a を 6 と -6 としてみた場合の表とグラフを上の図で表しているよ。
これを見ると a=6 のときは青線のグラフで書かれていて右上と左下にあるよね。
a=-6 のときは赤線のグラフで書かれていて左上と右下にあるね。
ようするに、反比例の関係\(y=\frac{a}{x}\)のグラフは
座標軸で交わらない2つの曲線でできているってことだね。
この反比例の関係\(y=\frac{a}{x}\)のグラフのような曲線のことを
双極線(そうきょくせん)っていうんだ。
これで、関数、比例、反比例は終わりになります。
ずいぶん長いブログになっちゃったけど、理解はしてもらえたかな?
まだ、?が残るようなら、どの辺が?なのかをはっきりさせて
そこをもう一度見直すようにしていこうね。
?を残したままにすると、これから?はどんどん増えていってしまうから
わからないをわかるにしてから次に進むようにしていってね。
では、今回はここまで。
ここまでの記事が良かったと思ったらここをクリックしてね。
質問なんかがあった場合はコメントにお願いします。
では、またさようなら。




コメント