どうも、こんにちはDKです。
今回は中学生1年生で習う平面図形の基礎、基本の作図についてやっていきますね。
作図って今までは、定規や分度器、三角定規なんかを使って、図形を書いたりしてたよね。
中学校では、分度器や三角定規を使わずに定規とコンパスだけを使って作図するんだね。
作図っていうのは、テストに出るのは、この単元での振り返りの時ぐらいで
この単元が終わってしまうと作図する機会は少なくなってしまうんだけど
ここでの作図はそれぞれの線分や角っていうのが、どういった形で図を作っているのかって言うのを
理解することができるんだ。
なので、作図はほどほどって思わずにしっかり、作図の仕方、ポイントを覚えておこう。
じゃあ、基本の作図始めていくね。
動画でも方程式の基礎を公開しているのでこちらも見てみてください。
※音が出るので、周りに気をつけて再生してみてね。
ひし形の特徴
まず、作図を行なっていくにあたって、このひし形について特徴を再確認しておこう。
このひし形が作図するのに、大事になってくるんだね。
まず、ひし形とは?ってところから見てみよう
・4つの辺の長さが等しい
・向かい合う辺が平行
ひし形っていうのは4つの辺の長さが等しくて、向かい合う辺が平行であれば
ひし形ってことになるね。これって正方形のことだよね。
ひし形は正方形も含むってことなんだね。
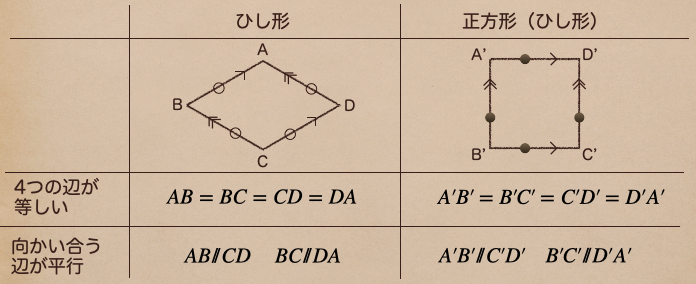
今回は正方形ではない方のひし形について考えていくよ。
この左側のひし形で対角線を引いた時、縦と横に対角線がひけるよね
この2本の対角線はそれぞれ、対称の軸になっているんだね
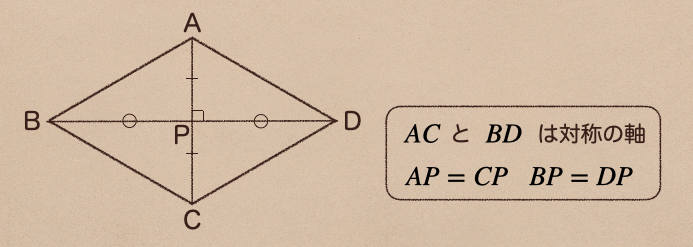
こんな風に、ひし形の対角線っていうのは、それぞれ、対称の軸となっているので
AP=CP、BP=DPってなるんだね、ようするに
線分AC、BDは垂直二等分線になるってことなんだね。
ひし形の特徴で押さえておくポイントは
・4つの辺が等しい
・対角線は垂直二等分線(対称の軸)となる
この2点を踏まえて、基本の作図やっていくね。
垂直二等分線の作図
じゃあ、まずは垂直二等分線の作図についてやっていくね。
垂直二等分線ってなんだっけ?って人は平面図形(1)を見てみてね。そっちで説明しているよ。
作図する方法なんだけど、さっき説明していたひし形の対角線っていうのが
実は垂直二等分線になっているんだね。ようするに
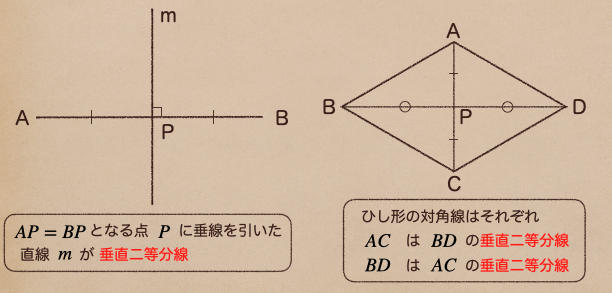
ひし形の特徴と垂直二等分線の特徴を見てみると次のことがわかるんだ。
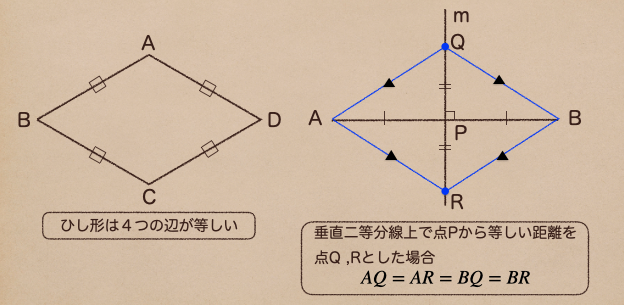
ここでポイントになってくるのが、右側の青い線でこれっていうのが
ひし形になっているってことなんだね。
ようするに、直線ABのAとBの点から等しい距離の点、上の図で言うQとRを線で結ぶと
垂直二等分線になるってことだね。
ここで、A、Bから等しい距離を引くのってどうするかっていうと。。。
コンパスを使うんだね。
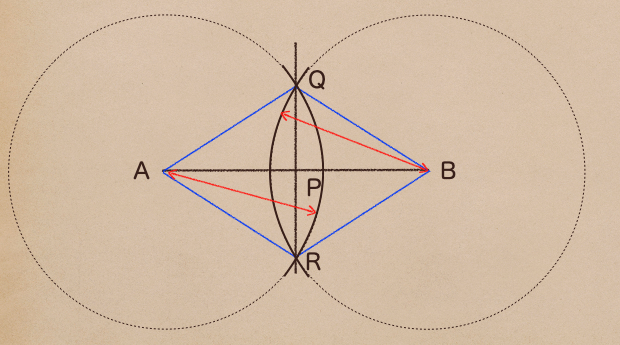
上の図のように点Aと点Bを中心としてコンパスで同じ大きさの円を書くと
赤い線は円の半径ってことになるから、円上はどこをとっても同じ長さになるってことだよね
点Aと点Bのそれぞれで書いた円が交差する点がQとRとなってこの2点を通る線っていうのが
垂直二等分線になるってことだね。作図する順番はこうだね。
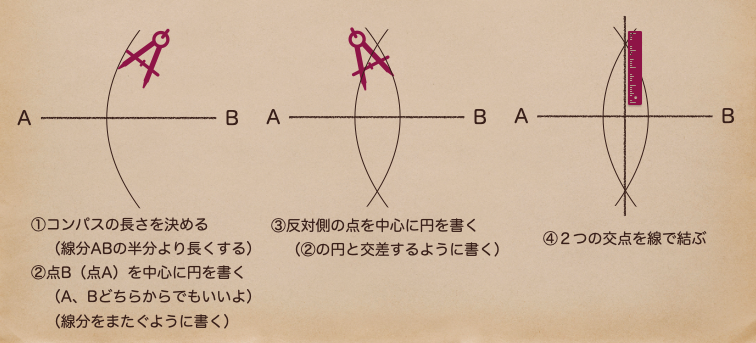
これで垂直二等分線がひくことができるんだね。
定規とコンパスを使って作図するっていうのはコンパスで長さが等しい円を書いて
交わる点を見つけるってことになるんだね。
次は角の二等分線の作図についてやっていくね。
角の二等分線の作図
角の二等分線っていうのは、その角を2等分する半直線のこと言うんだね。
図で書くとこんな感じだね。
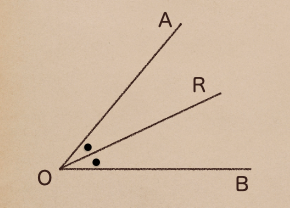
半直線ORが \(\angle\mathrm{AOB}\) の二等分線っていうことになるんだ。
ようするに、 \(\angle\mathrm{AOR}\) と \(\angle\mathrm{BOR}\) は同じ角って
ことになるんだね。
この角の二等分線の作図を考えてみよう。
また、ひし形に戻るんだけど、ひし形に対角線を引いた時の角についてみてみよう。
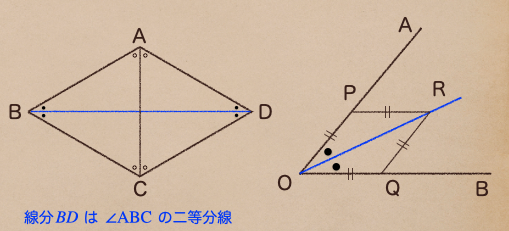
ひし形の対角線っていうのはそのひし形の角の二等分線になるってことなんだね。
この特徴をさっきの \(\angle\mathrm{AOB}\) の二等分線の図に当てはめて
考えてみると右の図のようになるんだね、こんな風にひし形を描くことができるってことなんだね。
これを使って作図をしてみるね。
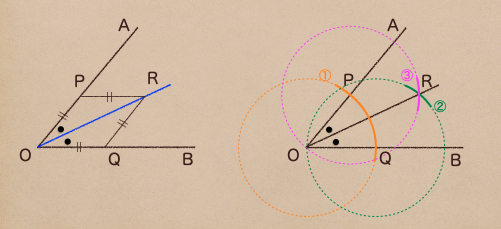
こんな風になるんだけど、円がいっぱいになってややこしいよね。
1つずつ見てみよう。
①点Oを中心に円を書いて、半直線AO、BOの交点を点P、Qとすると
線分OR、OQは長さが等しいことになるよね。
②点Qを中心として、①の時に書いた円と同じ大きさの円を書く
③点Pを中心として、①の時に書いた円と同じ大きさの円を書く
②と③で書いた円の交点Rとすると、これも線分 PR、PQの長さが等しいことに
なるね。さらに②と③で書いた円は①の円と同じなので
線分OP=OQ=PR=QRとなるんだね。ようするに四角形OPQRはひし形になるってことだね。
あとは、点Oから点Rに半直線を引けば、角の二等分線の出来上がりだね。
作図の順番はこうだね。
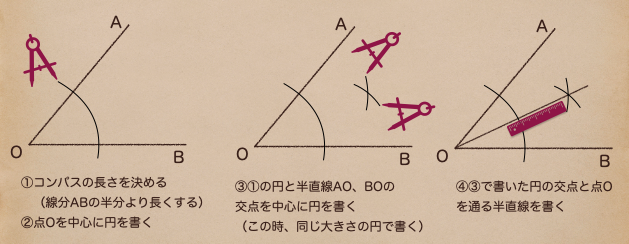
これで、角の二等分線が作図することができたね。
コンパスを使うことで、中心点から等しい長さを書くことができるってことが
わかっていれば、いろいろな図を作図することができるから試してみてね。
垂線
次は垂線の作図についてやっていくね。
垂直二等分線と同じじゃないの?って思うかもしれないけど
垂直二等分線は線分の中点に垂線を引いたものになるけど
垂線は線分上のどこにても引けるものも含まれるってことになるんだ。
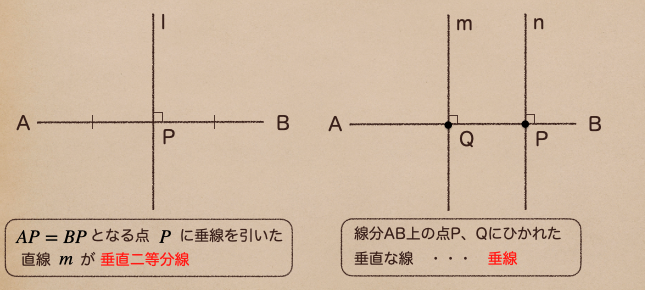
左の図はA、Bから等しい距離にひかれた垂線なので垂直二等分線になるね。
右側は点Pや点Qを通ってひかれた垂直な線になるので垂線っていう言い方になるんだね。
今回はこの右側の図の作図の仕方を学ぼう。
この垂線のひき方なんだけど、どこを通る垂線かによって作図の方法が変わってくるので
そのパターンを確認しておこう。
パターンは2種類で線分上にひかれた点を通るパターンと
線分とは異なる場所に置かれた点を通るパターンになるんだ。
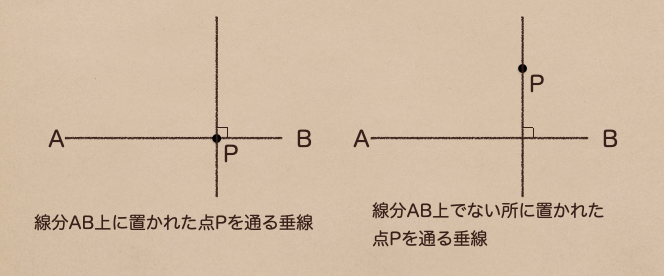
この2つのパターンについて垂線の作図を覚えてしまったら
いろいろな場面での作図を行うことができるよ。
この垂線のパターンもひし形を表すと
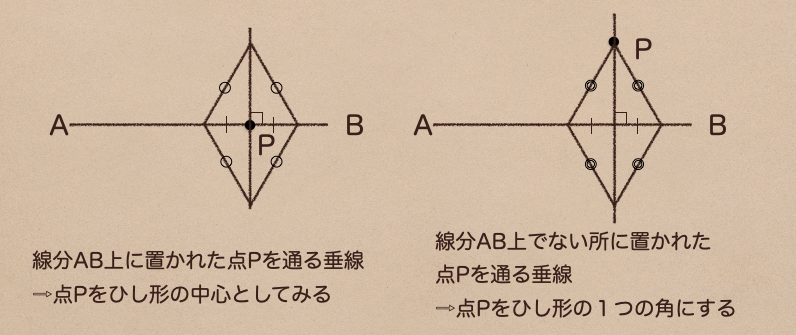
左側は点Pをひし形の中心して書くことができててるね。
右側は点Pをひし形の1つの角に書くことができるんだね
点Pを基準として、ひし形の角に当たる部分を決めてあげれば、垂線っていうのは作図することが
できるってことだね。
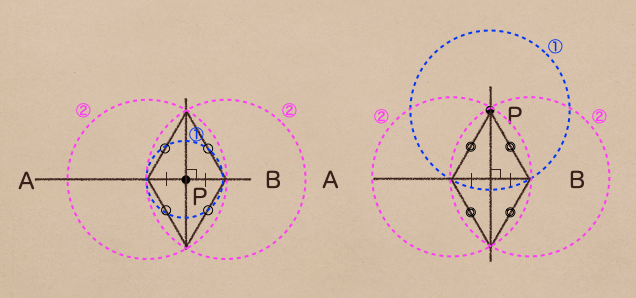
このひし形を作図するのは上の図のように
① 点Pを中心とした円を書く(右の図の場合は線分ABと接する大きさの円を書くよ)
② 線分ABと円①の接点を中心に円を2つ書く(線分ABとの接点は2つできるよ)
③ 2つの円②の交点を直線で結ぶ
これで、垂直ができるんだね。
線分AB上に点Pがある場合の垂線の作図の順番としては
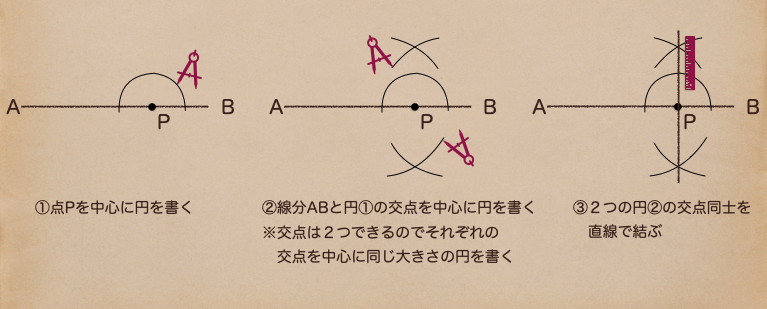
点Pから等しい長さの点を線分AB上に書いて、それを中心とした2つの円の交点を結ぶと
垂線がひけるってことだね。
線分AB上に点Pがない場合の垂線の作図の順番は
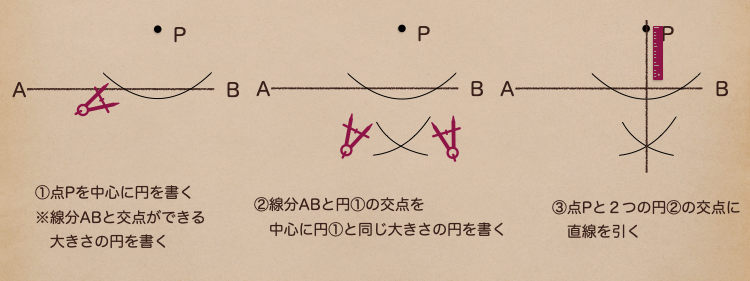
点Pを等しい長さの点を線分AB上に書いて、その点から同じ長さの交点と点Pを
結ぶと垂線がひけるんだ。
この2つのパターンで垂線がひけるようになれば、正三角形や、正方形なんかも
作図することができるから、どのような線を引いてあげると作図できるか考えてみてね。
じゃあ、今回はここまで。
作図ができるってことは、その図形の特徴をしっかり理解できていないと
むずかしくなってしまうかもだけど、逆にいうと作図できる=図形を理解している
ってことになるからここでは、図形の特徴を理解するってことも大事になるからね。
ここまでの記事が良かったと思ったらここをクリックしてね。
質問なんかがあった場合はコメントにお願いします。
では、またさようなら。




コメント