どうも、こんにちはDKです。
今回は中学1年生で習う空間図形をやっていきたいと思います。
空間図形ってなると平面図形を立体にした図形になってくるんだけど
今まで、平面で見ていた図形を立体で見るってなるのでわからないって人や
立体に図形を見るのが苦手って人もいるかもしれないんだけど、自分達の生活そのものが
立体になってるよね。だから、あまり苦手意識を持つのではなく、生活の中で
いろいろな立体を図にしてみるのもありかもしれないよ。
ここでは、基礎となる図形の名前であったりその性質っていうのを解説しているので
わからないところはじっくり読んでみて。
それじゃあ、早速やっていくね。
いろいろな図形
いろいろな立体についてサクッと学べる動画をやってるよ。
まずは、小学生でも習ってきた立体の呼び方についてやっていこう。
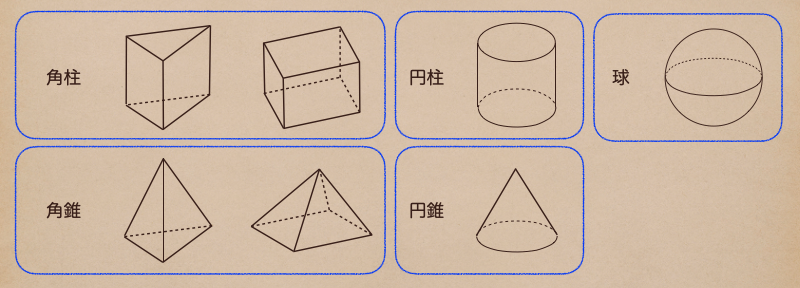
立体には大きく5つの形があって、角柱、角錐、円柱、円錐、球っていうのがあるんだね。
角柱っていうのは、底面と上面があってそれぞれが多角形になっている形
角錐っていうのは、底面が多角形になっていて、上面の部分は線が1点で交わる形
円柱は、底面と上面があって、円になっている形
円錐は、底面が円になっていて、上面の部分は線が1点で交わっている形になるんだね。
球っていうのはボールのような形を指しているよ。
それぞれの形と名前をしっかり覚えておこうね。
ちなみに、錐っていうのは「すい」って呼ぶんだけど、この字は「きり」とも読むことができて
先のとがったきりのこと指しているんだね。
この角柱の面にはそれぞれ、底面、側面っていう呼び方があって、角錐にも同じように
面の呼び方があるんだね。
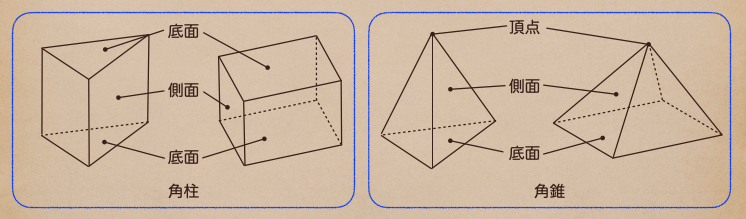
角錐の場合、1点に交わっているところを頂点っていう言い方をするんだね。
角柱の場合の、下の面は底面って言って、上の面は天面とか言うのではなく
同じ底面っていうのでここは気をつけよう。
この角柱や角錐っていうのは、底面が多角形になっている立体を言うんだけど
この多角形に柱や錐をつけて呼ばれることもあるから、覚えておこう。
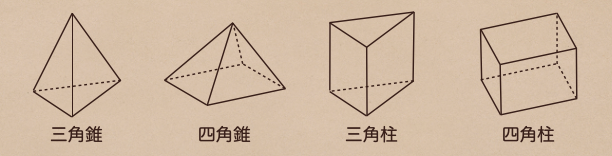
角柱や角錐っていうのは、他にも多面体と言う呼び方もしていて
この多面体っていうのがこう言った立体を指すんだ。
多面体・・いくつかの平面で囲われた立体
平面の数によって四面体、五面体、六面体と言う
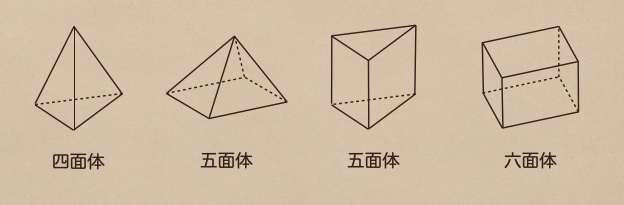
単純に平面の数で何面あるかで呼ぶので、底面が四角形でも三角形でも
平面の数が5つであれば五面体ってなるよ。
ちなみに、この多面体の中で、すべての面が合同となる正多面形で
どの頂点に集まる面の数も等しく、へこみのないものを正多面体っていうんだけど
この正多面体は今までに5種類しかないんだって。
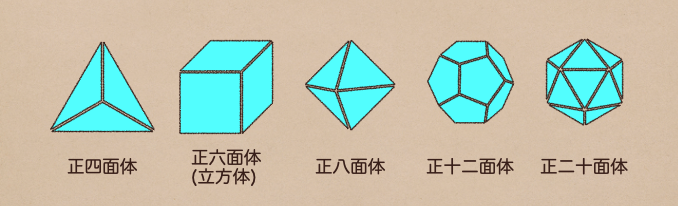
ここまでに出てきた立体の呼び方っていうのは、この空間図形の問題の中で
よく使われることになるから、形と呼び方をしっかり覚えておこう。
次は見取図と展開図をやっていくね。
見取図と展開図
見取図と展開図についてサクッと学べる動画をやってるよ。
見取図と展開図っていうのは
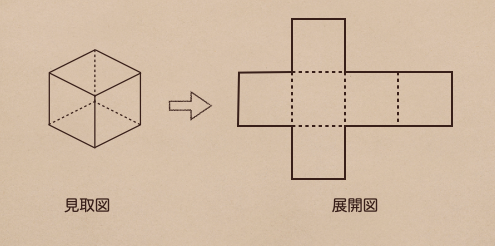
立体の図形を見取図って言って、その立体図形を開いて平面図で表したものを展開図っていうんだね。
これをさっきの角柱、角錐の場合の展開図と円柱、円錐の展開図を見てみよう。
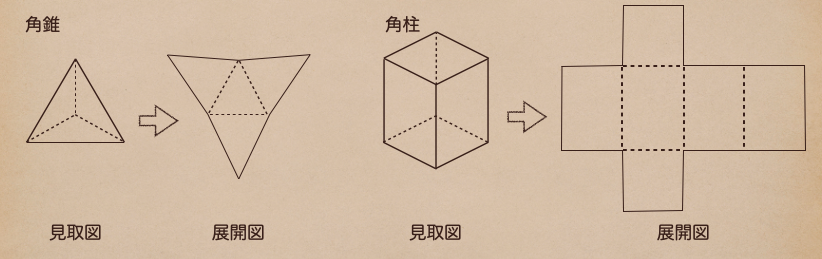
角錐と角柱の展開図は図のとおりでそれぞれに
角錐・・底面は1つの多角形、側面は三角形
角柱・・底面は合同な2つの多角形、側面は長方形
っていう特徴があるんだね。底面の多角形が五角形、六角形ってなっても
側面の形は角錐が三角形、角柱は長方形は変わらないよ。
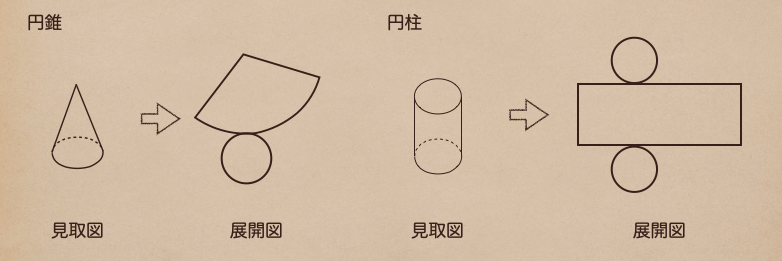
円錐と円柱の展開図は図のとおりでそれぞれに
円錐・・底面は1つの円、側面はおうぎ形
円柱・・底面は合同な2つの円、側面は長方形
円錐の展開図はおうぎ形になるってところが他の立体とは違うところになるから
覚えておこう。
角柱も円柱もどちらも、底面は「合同な」ってつけているんだけど
同じ形になっているってこともポイントだよ。
ここでやった展開図っていうのは、空間図形の問題ではよく問題になるところだから
立体を展開させたときの図がどうなるかを色々確認してみよう。
次は空間内の平面と直線についてやっていこう。
2直線の位置関係
見取図と展開図についてサクッと学べる動画をやってるよ。
空間内で次の場合を考えてみよう
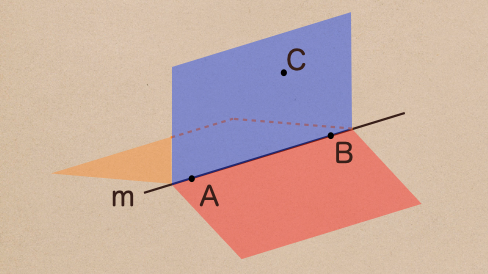
上の図で直線m上に点Aと点Bがあってこの2点を含む平面っていうのは
青い平面、オレンジの平面、赤の平面すべてってことになるけど
ここに点Cを含む平面は?ってなると青い平面しかないんだね。
これっていうのがポイントで
同じ直線上にない3つの点を通る平面は1つしかない
ってことなんだ。これって空間図形の特徴の1つなので覚えといてね。
今回は点と平面の関係だったんだけど、直線と平面にもこんな特徴があるんだ。
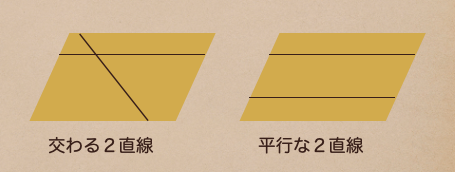
「2つの直線が交わっている」や「2つの直線が平行」が含まれる平面っていうのも
1つしかないってことなんだね。
これだけ、言われるとふーんってなっちゃうと思うので、立体をつかって説明するね。
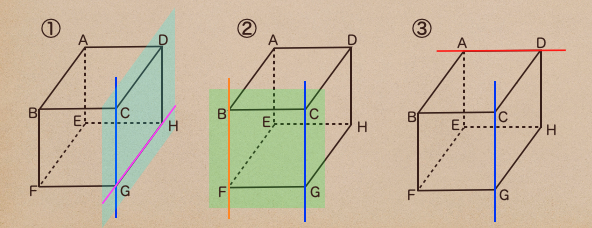
①の場合だと、直線CGと直線GHは交わっているよね。
そして、直線CGと直線GHは平面CGHD上にあるよね。
②の場合だと、直線CGと直線BFは平行になってるよね。
そして、直線CGと直線BFは平面BFGC上にあるよね。
こんな風に、2直線が交わっているもしくは、平行である時、その2直線は
同じ平面上にあるよってことなんだね。
じゃあ、3はどうなっているかっていうと、どうかな?
直線CGと直線ADは交わっていないし、平行でもないよね。
そして、直線CGと直線ADは同じ平面上にないよね。
これっていうのも、空間上の直線の特徴で
空間上の2直線が交わらず、平行でないとき2直線は平面上にない
また、この2直線はねじれの位置にあると言う
ってことが言えるってことなんだね、逆に言うと
ねじれの位置にある2直線は平面上にないってことにもなるよ。
空間上にある直線の位置関係っていうのはわかったかな?
次は直線と平面の関係を見ていくよ。
直線と平面の位置関係
今度も、立体を使って確認していくね。
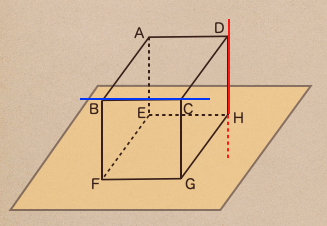
・直線BCと平面EFGHは交わらない時、直線BCと平面EFGHは平行であると言う
・直線DHと平面EFGH上のその直線をとってみても垂直である時
直線DHと平面EFGHは垂直であると言う
この直線DHは平面EFGHは垂線と言う
直線と平面の位置関係っていうのは2直線の位置関係と同じことが言えるってことだね。
直線と平面が垂直であるっていうところでは、こんなことも言えちゃうんだ。
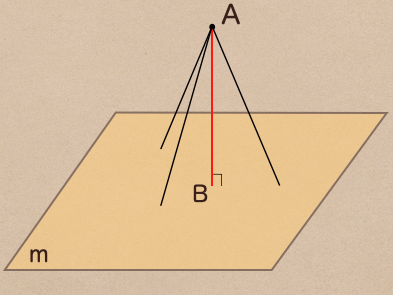
上の図で点Aから平面mに直線っていうのは色々と引くことができるよね。
この中で平面に垂線な線分ABって言うのを引いた時この線分ABって言うのを
点Aと平面mとの距離っていうんだね。
この平面までの距離っていうのを今度は立体に当てて、見てみるね。
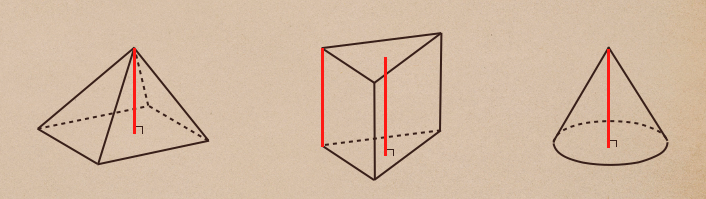
立体で角錐(左)や円錐(右)の場合、頂点から底面に垂直に引いた線分や
角柱(中)のように底面から底面まで垂直に引いた線分っていうのをそれぞれの立体の
高さって言うんだ。
角柱では、縦に引いた線分っていうのが、底面から底面まで垂直に
引いた線分ってなるから、この縦に引いた線分が高さってことになるんだね。
この高さって言うのは、これからもよく出てくるから
どこの部分を指して高さと言っているかっていうのをしっかり理解しておこう。
2平面の位置関係
2つの平面でも位置関係っていうのは考え方は一緒だよ。
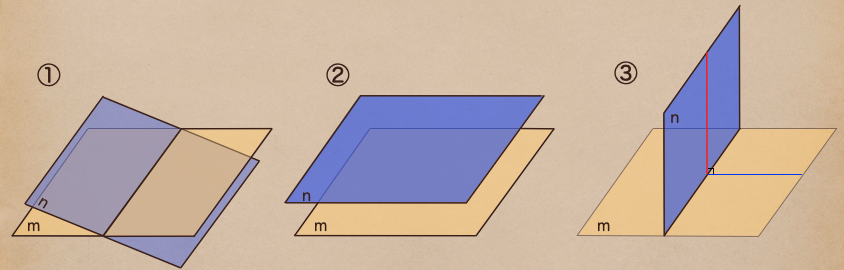
①は2つの平面が交差しているよね、これを交わるっていうんだ。
この交わった時の線っていうのは直線になることが特徴だね。
②は2つの平面は平面mと平面nが交わらない状態にあって
これを平面mと平面nは平行であるって言うんだね。
③は平面mと平面nが交わっていて、平面nに引かれた直線が平面mと垂直になっている時
平面mと平面nは垂直であるって言うんだね。
ここでも、2直線の位置関係や平面と直線の位置関係と一緒で
2つの平面の位置関係にも、交わる、平行、垂直な関係があるってことだね。
次は立体のいろいろな見方についてやっていくね。
面を平行に動かしてできる立体
立体のいろいろな見方、投影図についてサクッと学べる動画をやってるよ。
角柱や円柱っていうのは、多角形や円を面に対して垂直な方向に
平行に動かした時にできる立体となってよね。
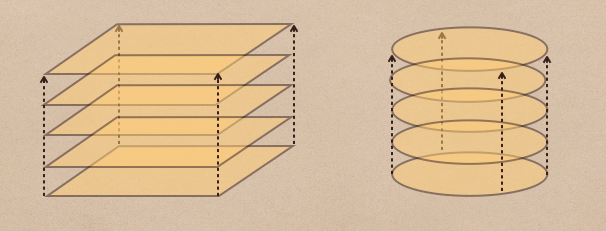
ようするにこれっていうのは、底面の平面を積み上げていくと立体になって
それっていうのが角柱や円柱になるってことなんだね。
角柱や円柱っていうのは、平行な平面の集まりってことになるので
底面と平行に断面を見た時、ずっと底面と同じ形になっているってことにもなるんだ。
面を回転させた立体
今度は、下の平面を回転させた時にどんな立体になるか見てみよう。
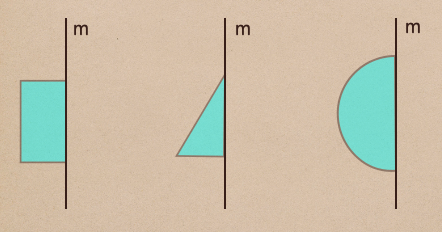
左から、長方形、三角形、半円を回転させるんだけど
回転させるのは直線mの周りえを1回転させるんだよ。そうすると。。
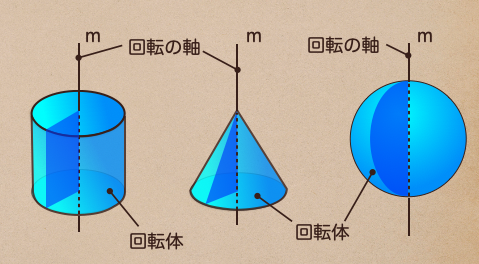
長方形は回転させると、円柱に。三角形は回転させると、円錐に。
半円を回転させると、球になったね。
こうやって、回転させてできた立体っていうのは、回転体って言うんだね。
そして、この直線mって言うのが回転の軸っていう言い方をするんだ。
回転の軸を使って、回転体はいろいろな平面で使うことができるから
自分でも、身の回りのものを平面から回転体にしてみたら
どんな立体になるか試してみよう。
線を移動させてできる立体
今度は、回転したり、平行に動かすのではなく
線分を動かしてできる立体についてだよ。
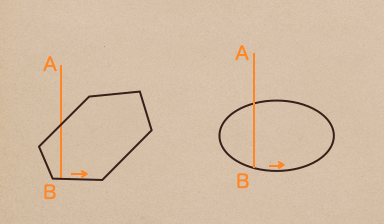
こんな風に底面にある平面の線上を線分AB が1周した時にどんな立体に
なるか、考えてみよう
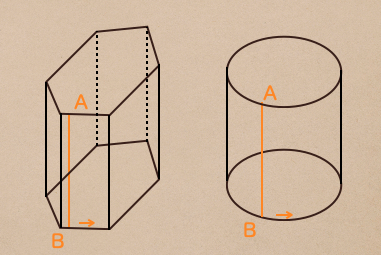
角柱と円柱ができたね。
こんな風に1周させて立体と描いた、線分ABって言うのは
角柱や円柱の母線って言う言い方をするんだね。
この母数っていうのは、今回のように垂直に引いた線分だけではなくて
一点から底辺の線分上に沿って描くこともできるんだね。
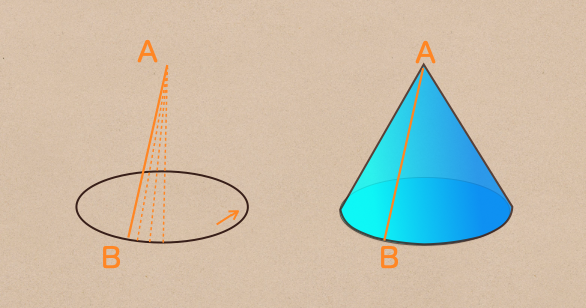
こんな風に、円錐を描くこともできるんだ。
この円錐を描いた時の線分ABって言うのも、円錐の母線ってことになるんだね。
立体の投影図
ここからは投影図(投影図)って言うのをやっていくよ。
この投影図は、立体を平面に映し出して(投影)したものを図として表すことなんだ。
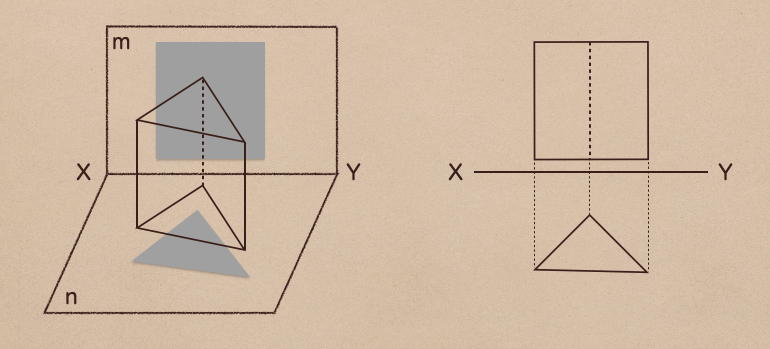
左の図のように直線XYに垂直に交わる平面mとnに対して
側面手前から光を当てたら、平面mに影ができるよね
同様に上側の底面から光を当てると平面nに影ができるって具合に
手前からと上側から見た時の形状を図に書き込むと右側のようになるんだね。
これを投影図っていう言い方をするんだね。
この投影図の正面から見た図を立面図(りつめんず)
真上から見た図を平面図って言う言い方をするんで、ここはしっかり覚えておこう。
投影図を書くときの注意点としては線の引くときに
実際に見えている線を実線で記載して
実際に見えないけど、角部があったりしたときは破線を使うようにして
使い分けるようにしよう。
はい、ではここまでが空間図形についてでした。
ここまでの記事が良かったと思ったらここをクリックしてね。
質問なんかがあった場合はコメントにお願いします。
では、またさようなら。




コメント