どうも、こんにちはDKです。
中学生で習う数学の基礎を解説しているよ。
今回は中学2年生で習う、『平行と合同』についてになるよ。
ここでは、「角と平行線」でこの『平行と合同』入門にあたる部分で
図形における性質っていうもの解説していて、ここをしっかり押さえておかないと
この単元の最後の方にある、証明ってところでつまずいてしまうので
「角と平行線」の基礎をしっかり理解しておく必要があるんですね。
これから学ぶ人は予習として、一度、学んだことのある人は復習に
活用していってください。
動画でも基礎の解説行っているので、よかったらそっちと一緒に見てもらえると
より、理解が深まるかも。(注意:音が出るよ)
では、さっそく始めていきますね。
(1)いろいろな角
まずは、下の図のように直線 \(l\) と直線 \(m\) が交差するようにあって
この交差している所の角度をそれぞれ、\(a,b,c,d\)としたとき
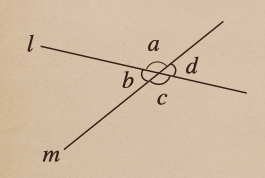
この時の、\(\angle a+\angle b\) っていうのは \(180^\circ\) になるよね。
これは直線 \(m\) 上にある2つの角 \(\angle a\) と\(\angle b\) なので、その和は
直線となるので、\(180^\circ\) ってことだったよね。
同様に、\(\angle a+\angle b\) は?って言うと、これも同じく\(180^\circ\) となるんだね。
これは直線 \(l\) 上にある2つの角 \(\angle b\) と\(\angle c\) ってことだね。
こんな風にみていくと、それぞれの角の和っていうのは
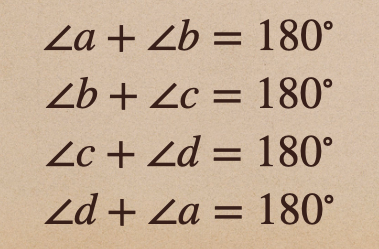
隣り合う同士の角の和はすべて \(180^\circ\) になるってことなんだね。
ここで、 \(\angle a + \angle b=180^\circ\) と \(\angle b + \angle c=180^\circ\) に
注目してみると、同じ \(\angle b\) が含まれているよね、これって言うのが
\(\angle a\) と \(\angle c\) は同じ角ってことになるんだね。
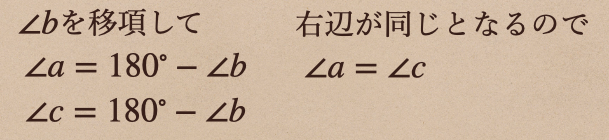
同じようにみると、 \(\angle b + \angle c=180^\circ\) と \(\angle c + \angle d=180^\circ\) は
同じ\(\angle c\) が含まれて、これは\(\angle b\) と \(\angle d\) は同じ角ってことが言えるんだね。
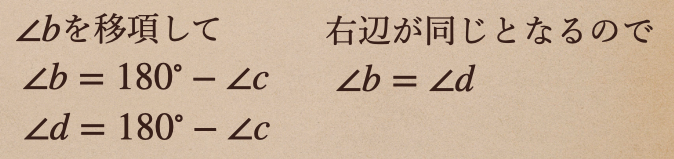
初めの直線と角の図形に戻ってみると、交差した直線でその交差した部分のそれぞれの角のうち
向かい合っている角って言うのは等しいってことだ言えるんだね。
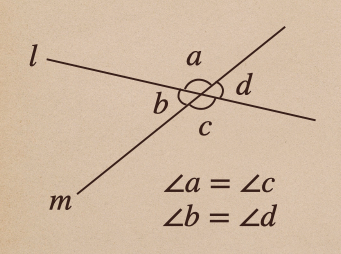
こんな風に向かい合う角どうしを対頂角って言うんだね。
\(\angle a\) と \(\angle c\) は 対頂角
\(\angle b\) と \(\angle d\) は 対頂角
そして、対頂角の性質としては、次のことが言えるんだね。

これが一つ目の角に対する性質ってことになるので、しっかり理解しておいてください。
今度は、直線を3本で交差した時の交点の角を書いてみると
それぞれの角を \(\angle a\) 〜 \(\angle h\) としたとき
\(\angle a\) と \(\angle e\) は同位角(どういかく)であるって言うんだね。
また、\(\angle c\) と \(\angle e\) は錯角(さっかく)であるって言うんだね。

この角の位置によって、同位角、錯角っていうので、この言葉とどことどこの角を
言っているのかっていうのをしっかり覚えておこう。
(2)平行線と角
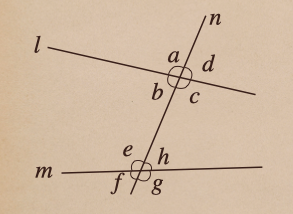
(1)いろいろな角で解説していた、3本の直線の中で、直線 \(l\) と直線 \(m\) が平行で
あった場合について、見ていきますね。
この平行な2直線 \(l,m\) に交差した直線 \(n\) の交点の角っていうのは
これにも、性質があって
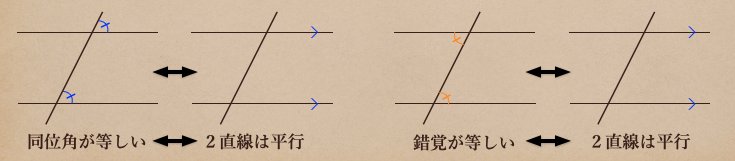
[平行線の性質]
2直線に1つの直線が交わるとき
①2直線が平行なら、同位角は等しい
②2直線が平行なら、錯覚は等しい
ってことが言えて、さっきの図でみるとこう言うことになるんだね。

また、逆の言い方もできて、同位角、錯覚が等しい場合、その2直線は平行ですよって
言うことが言えるってことになるんだね。
[平行線であるための条件]
2直線に1つの直線が交わるとき
①同位角が等しければ、その2直線は平行である
②錯覚が等しければ、その2直線は平行である
どちらかを説明できれば、もう片方も説明できるってことになるんだね。
(3)三角形の角
次は三角形の角についてみていきますね。
まずは、この図を見てみて
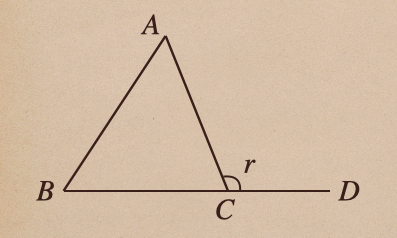
三角形ABCがあって、線分BC上の延長線上にDまで線を引いてる図になるね。
この時の \(\angle ACD\) を \(r\)として、この\(r\) を求めたいってなっても
これ以上のことがわからなければ、求めることができないよね。
じゃあ、ここで、線分ABと平行な線をCを通るように引いて
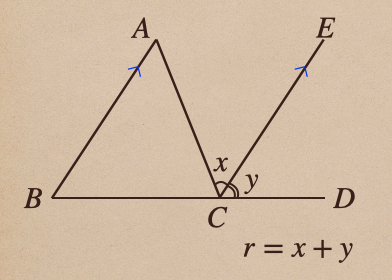
\(\angle ACE = \angle x\) 、\(\angle ECD = \angle y\)としてみた時
平行線の性質から、\(\angle BAC=\angle ACE\)となるんだね。
これは平行な2直線 の場合は錯覚が等しいってことから\(\angle BAC=\angle ACE\)に
なるってことですね。
同様に、\(\angle ABC = \angle ECD\)となって、これは2直線が平行なら
同位角は等しいってところから、\(\angle ABC = \angle ECD\)が言えるってことなんですね。
ようするに、\(r=\angle BAC+\angle EDC\)になるってことなんだね。
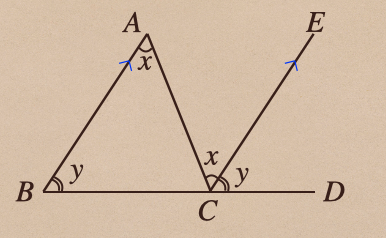
この三角形の角 \(\angle BAC\) 、\(\angle ABC\) 、\(\angle BCA\)のことを内角と言って、
三角形の辺とそのとなりの辺の延長とがつくる角を外角っていう言い方をするんだけど。

この外角っていうのはそのとなりあう内角以外の内角の和になっているってことなんだね。
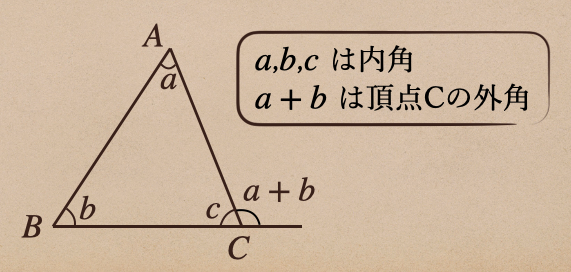
ここで、三角形の性質を紹介しておくね。
[三角形の内角と外角の性質]
①三角形の内角の和は180°
②三角形の1つの外角は、その外角ととなり合わない2つの内角の和に等しい
(4)図形の性質と補助線
ここまでで、同位角、錯覚、平行線の性質、三角形の性質を理解してもらえたかと
思うんだけど、それらを踏まえて、こんな問いがあった場合を考えてみよう。
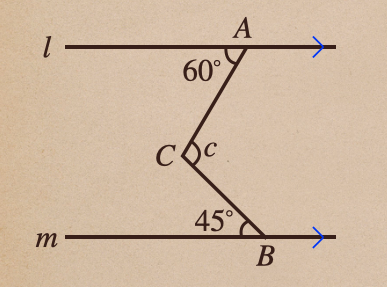
\(\angle c\) はいくつかってことなんだけど、分度器なんかを使えば
求めることができるんだけど、分度器を使わずにってなった場合
今のままで、求めていくことはむずかしいよね。
なので、こんな時は補助線を引いて、今までに解説してきた
図形の性質を使って、求めていく必要があるんだね。
じゃあ、どこにどんな補助線を引くかってことなんだけど
答えはなくて、好きなように補助線(ほじょせん)を引けばいいってことになるんだね。
ただ、問いである \(\angle c\) を求められるように図形の性質が使えるように
していこう。
ここでは、何パターンかの補助線を引いて、どんな図形の性質を使っているかっていうのを
見ていきますね。
①補助線に平行線をひく
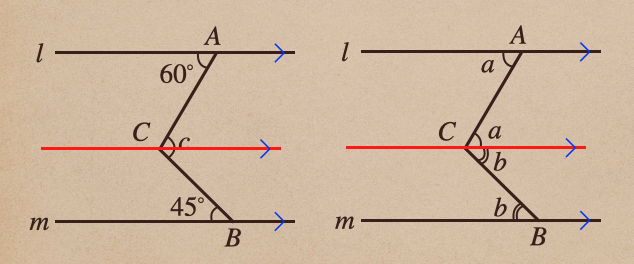
平行線をひくのはCを頂点としたところにひこう
そうすることで右の図のように \(l\) と \(m\) と補助線で平行な2直線となって
「錯覚が等しい」を使って、\(c\) は\(a+b=60+45=105\)° と求めることができるんだね。
②補助線に延長線をひく
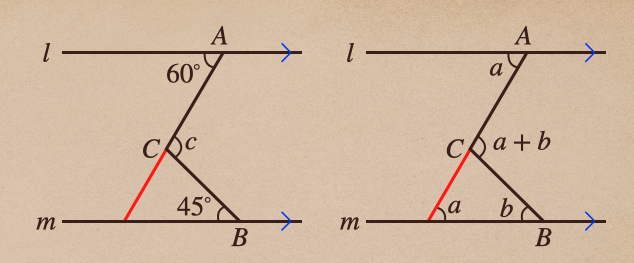
線分ACの延長線を直線 \(m\) までひくんだね、
右の図のように補助線をひいたことで、三角形ができて「錯覚が等しい」ことから
直線 \(m\) と補助線の角は \(a\) となって、三角形の性質から
「外角ととなり合わない内角の和は等しい」ことから \(c\) は \(a+b=60+45=105\)° と
求めることができたってことだね。
③補助線に垂線をひく

垂線を頂点Cに接するように線をひいてあげることで
三角形が2つできて、垂線で引いたので、「三角形の内角の和は180°」から
頂点Cの角が求められて、頂点Cの3つの角の和は180°となるので
求めたい \(\angle c\) は \(a+b=60+45=105\)° となるってことですね。
①〜③の補助線どれを引いても、 \(\angle c=105\)° となっていたね。
なので、どんな補助線をひいても、求めることができるってことなんだね。
ただ、①、②、③の順に求め方がややこしくなっていっているので、
この場合、①の平行な補助線をひく方が求め方がおすすめですね。
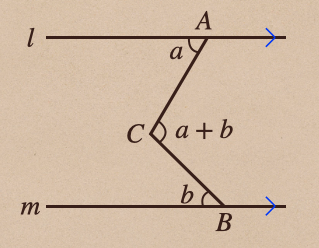
ちなみに、今回、求めた頂点Cっていうのは \(a+b\) になるってことも覚えておくと
わざわざ補助線をひかなくても求めることができるので、覚えておきましょう。
(5)多角形の内角
今度は、多角形の内角についてですね。
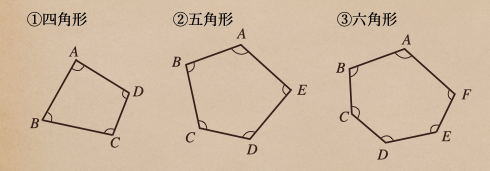
多角形でも、内側の角のことを内角っていうので、覚えておこう。
この多角形の内角の和はいくつかって聞かれたら、四角形なんかは
今までも、よく使ってきていたから、360°ってすぐに言えるけど
五角形は?六角形は?ってなった時は、すぐには答えられないよね。
内角の和を確認したいって時は、三角形を作るように補助線をひいてあげるんだね。
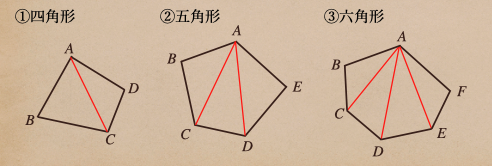
こんな風に、補助線をひくことができて、それぞれの多角形で三角形の数は
①四角形は2つ、②五角形は3つ、③六角形は4つになったるよね。
それと、どの多角形も、補助線をひいて作った三角形の内角っていうのは、
その多角形の内角および、内角の一部になっているんだね。
ようするに、この三角形の内角の和とその個数をかけてあげることで
多角形の内角の和を求めることができるってことなんだね。
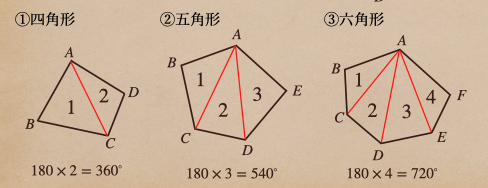
それぞれの多角形の三角形の数に注目してみると
辺の数が増えると、三角形の数もそれに応じて、増えていっているのがわかるよね。
これっていうのが、法則があって
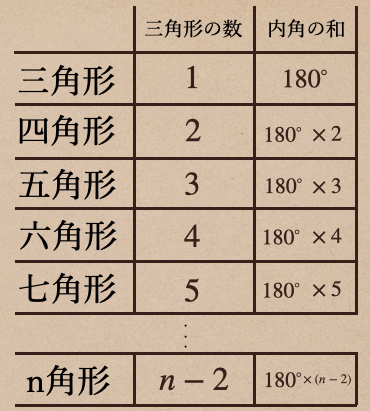
多角形の辺の数から2を引いた数っていうのが、その多角形の三角形の数に
なっているってことになるんだね。
そして n 角形のところを見ると、内角の和っていうのは
\(180×(n-2)\) として求めることができるってことなんだね。
[三角形の内角と外角の性質]
n角形の内角の和は、\(180×(n-2)\)° となる
この公式を覚えていなくても、補助線をひいて、三角形の数を
見てあげれば、内角の和っていうのは、求めることができるので
多角形は三角形を作るってことを理解しておければ、オッケーだね。
(6)多角形の外角
今度は、多角形の外角について見ていきましょう。
多角形の外角っていうのも、三角形の外角と同じ考え方で
一つの辺とそのとなりの辺の延長とでつくる角をその頂点の外角と言うんだね。

図の赤色で表した角がそれぞの頂点の外角ってことになるってことだね。
じゃあ、多角形の外角の和はいくつになるかっていうのを見てみよう。
多角形の外角を知りたい場合っていうのは、こうやって求めることができるよ。

頂点の内角と外角の和っていうのは、直線になるよね
だから、頂点の内角と外角=180°ってことだね。
四角形なら、頂点が4つあるってことなので、4をかけて
それを内角の和である360°で引いたら、外角の和になるよってことだね。
同様に五角形、六角形も計算してみると。。
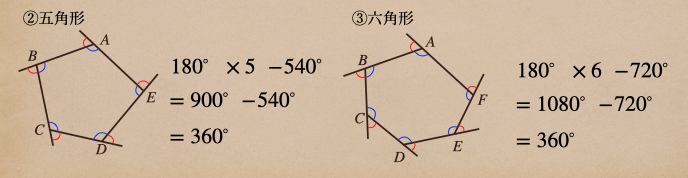
四角形も五角形も六角形も外角の和はすべて360°になったね。
これっていうのが
[多角形の外角の和]
n角形の外角の和は、\(180\)° となる
ってことなんだね。ようするに、多角形の外角の和はすべて360°になるってことなんだね。
ちなみに、ここには、三角形も含まれていて、三角形の外角も360°になるんだね。
今回は、ここまでになります。
ここまでの記事が良かったと思ったらここをクリックしてね。
質問なんかがあった場合はコメントにお願いします。
では、またさようなら



コメント