どうも、こんにちはDKです。
今回は方程式の基礎をやっていくよ。
動画でも方程式の基礎を公開しているのでこちらも見てみてください。
※音が出るので、周りに気をつけて再生してみてね。
この方程式では、正の数、負の数の四則計算や文字式をたくさん使っていくから
まだ、正の数、負の数や文字式に不安のある人は僕のブログの正の数、負の数や文字式を見てみて。
わからないまま進めるのと、わかってから進めるのでは、ここ方程式の理解は大きく変わってくるから
わかったを一つでも多く作ってから学んでいこうね。
では、やって行こう。
方程式とその解
方程式って?解って?ってところから説明していくよ。
まずはこれを見てみて。
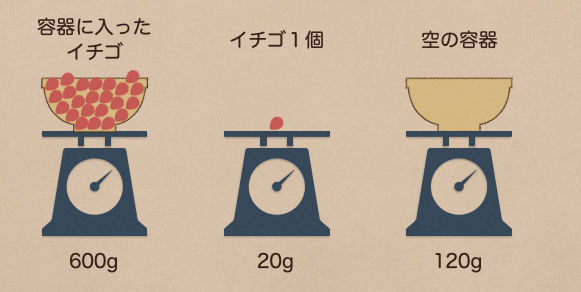
容器に入ったイチゴがあるよね?この重さが600gみたいだね。
イチゴ1個の重さは20gだね。
それと、容器の重さが120gってなってるね。
じゃあ、この時のイチゴの量は何個になるかな?
ここで、文字式と等式を使って式を作ることができるよね。イチゴの個数を \(x\) とした場合
式は \(20x+120=600\)・・① になるよね?ここまではいいかな?
この①のようにわかっていない文字 \(x\) を含む等式を方程式って言うんだ。
この方程式 \(20x+120=600\) の \(x=24\)を代入して式の値を求めてみよう。
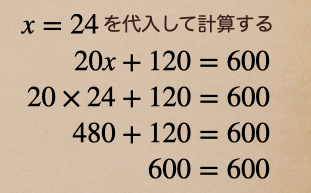
\(x\)を代入して計算すると \(600=600\)と方程式①を成り立つよね。
こんな風に方程式を成り立たせることができる文字の値をその方程式の解って言うんだ。
そして、方程式の解を求めることを方程式を解くって言い方をするよ。
ここの方程式や解(方程式を解く)って言い方はよく出てくるから
しっかり覚えておこう。
方程式となる等式にはこんな性質もあるんだ。

重さのわかっていない箱と1gのおもり3個と1gのおもり10個がてんびんがちょうどつり合っている
とするね。箱の重さを \(x\) gとするとてんびんの両方の重さはつり合っていることから
\(x+3=10\)って方程式が作れるよね。

この方程式 \(x+3=10\) の両辺から3(g)をひいた残りの重さが等しくなるよね。

\(x=7\) となって、箱の重さが7gってことがわかったよね。
こんな風に等式っていうのは両辺から同じ数をひいても等式が成り立つっていう性質があるんだ。
他にも性質があってまとめると、こういうことだね。
等式の性質
①等式の両辺におなじ数をたしても、等式は成り立つ
A = B なら A + C = B + C
②等式の両辺から同じ数をひいても、等式は成り立つ
A = B なら A – C = B – C
③等式の両辺から同じ数をかけても、等式は成り立つ
A = B なら A × C = B × C
④等式の両辺から同じ数をわっても、等式は成り立つ
A = B なら A ÷ C = B ÷ C
この等式の性質を用いて方程式を解いて \(x\) の値を求めるんだ。
それぞれの性質をもとに例題を見てみよう。

①から④の例題でポイントとなるのが、それぞれの方程式で解と求める場合 \(x=oo\) が
知りたいってことだよね。だから、どの例題も両辺にたしたり、ひいたりしている数は
\(x\) だけが残るようにしているってことだね。
次は方程式の解き方についてやっていくね。
解き方の方では、ここで学んだ等式の性質をもとにした解き方になっているから
等式の性質はしっかり理解してから、次に行こうね。
方程式の解き方
等式の性質は理解できたかな?
じゃあ、この性質を使って解いた時に式がどのように変わっていくかを見てみよう。
まずは、\(3x-12=9\) を解いてみよう。
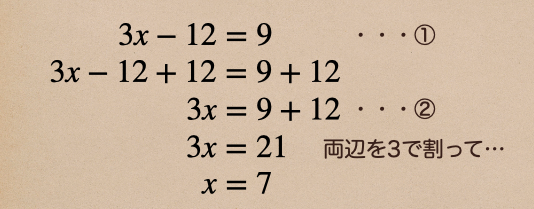
ここで、①の式と②の式を見てみるとあることに気づくよね?
そう、左辺にあった−12が右辺で+12となって移っているんだね。
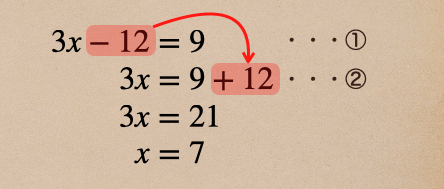
こんな感じで、左辺から右辺に符号を変えて移すことができるんだね。
これを移行するって言うんだ。
この移行をすることで方程式を簡単にして、解を解くことができるんだね。
\(8x-4=5x+8\) の式の場合、どうやって移行して解いていくのがいいかな?

両辺に文字の項がある式では、左辺に移行させて数の項は右辺に移行させて
計算して解いてあげると計算しやすくなるよ。
もう少し、例題をやっておこう。

例題1のようにかっこがある方程式はまずかっこを外してあげよう。
かっこを外すときは…覚えてるよね。分配法則を使うってこと忘れずにね。
例題2は分数が出てきているね。この場合はまず分数をなくしてしまおう。
そのためには、両辺に分母の公倍数をかけてあげるんだね(例題2の場合、3と4の公倍数12だよ)
例題1も例題2もややこしく見えるけど、1つずつ解いていけば、やっていることは一緒だから
1つずつ確実に解いていこうね。
今回の計算をしていく中で \(ax=b\) のような式が出てくるよね。
例題1では \(-2x=12\) や \(x=-6\)、例題2では \(x=20\) のことだね。このような形になる
式を一次方程式って言うんだ。
この一次方程式の解く順番をおさらいしておくね。

ここまでが、方程式の解き方についてだよ。ちゃんと理解できたかな?
まだ、理解できていないようなら繰り返し見て、練習問題を解いてみよう。
自分がどこがわからないかをしっかり理解することも、苦手をなくす大事な作業になるからね。
じゃあ、次は比と比例式についてやっていくね。
比と比例式
次は比と比例式についてやっていくね。
比って言うと小学校6年生でも習ったと思うんだけど、多くの人が苦手としている部分に
なるんじゃないかな。逆に言えば、苦手な人が多いところで得意にできれば周りからも
差をつけることができるよね。なので、わからないをわかるにしていこう。
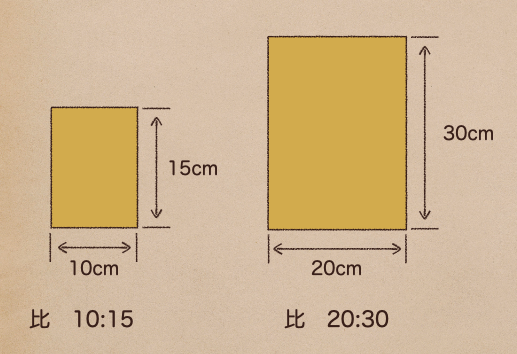
上の図のように長方形があった場合、この長方形のタテとヨコの比は10:15となるよね。
この、比10:15の10や15を比の項で言うんだね。
また、比10:15の前の項10を後ろの項15でわった\(\frac{10}{15}=\frac{2}{3}\)を
比の値って言うのも覚えておこう
大きい方の長方形の比は20:30だよね、これも比の値は\(\frac{20}{30}=\frac{2}{3}\)に
なるよね。ってことは10:15と20:30は等しいってことになるんだ。
この等しい関係を式で書くと10:15=20:30ってなるんだけどこれを比例式って言うんだね。
もう一度、整理しておくよ。
比 a : b で a や b を比の項と言う
比 a : b の前の項 a を後ろの項 b でわった値 \(\frac{a}{b}\) を比の値と言う
a : b = c : d のように比が等しいことを表す式を比例式と言う
ここまではいいかな?
じゃあ、\(x\) : 50 = 1 : 5 っていう比例式があったときに
\(x\)の値はどのように求めることができるかな?
この場合は左辺、右辺の比を比の値にしてみよう。 \(\frac{x}{50}=\frac{1}{5}\)ってなるね。
あとは\(x\)を解いてあげるだけだね。\(x=10\)だね。
こんな風に比例式に含まれる文字を求めることを比例式を解くって言うんだ。
比例式にも性質があって、覚えておくと計算がぐんと楽になるからおぼえておこう。
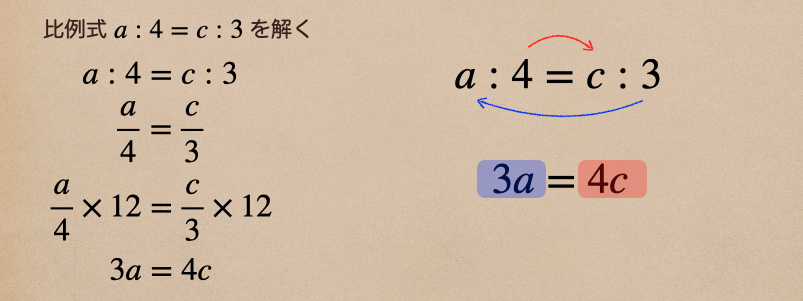
比例式を解くと図の式のようになるよね。ここで注目したいのは 3a = 4c ってところだね。
これって、比例式の内側の積と外側の積が等しいことを表しているんだね。
図で言うと右側のことだよ。
ようするに、比例式は内側の積と外側の積は等しいってことだね。
ここまでが、方程式についてだよ。理解できたかな?
この方程式はこの基礎を理解することはもちろんだけど、応用が非常に重要になるんだね。
特に文章問題から、自分で方程式を作って、解くってことまでやっていかなければならないよ。
文章問題は数をこなして、方程式を作ることに慣れていくのが
一番だから理解できたら問題を解いていこう。
ここまでの記事が良かったと思ったらここをクリックしてね。
コメントもくれるとうれしいな。




コメント