どうも、こんにちはDKです。
このブログでは、中学数学の基礎を学ぶをテーマに基礎となるところの
解説を行なっています。
ここから各学年、各単元を選んで、基礎を学ぶページに飛べるので
よかったら一度、みてみてください。
今回は、中学2年生で習う「平行と合同」の証明の根拠となる図形の性質を
まとめてみたので、確認したいなって思ったら、ここで確認してみてください。
(1)対頂角(たいちょうかく)の性質
対頂角は等しい
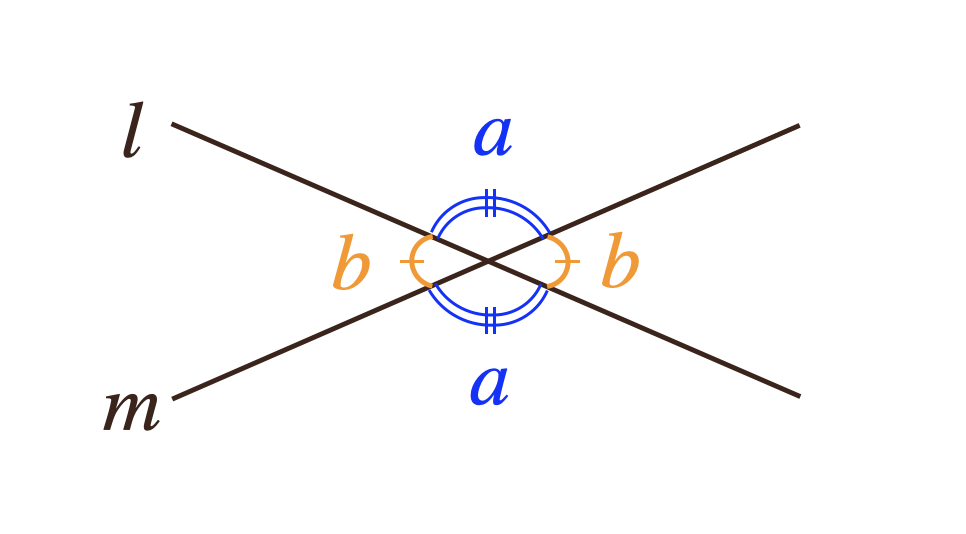
(2)平行線の性質
2直線に1つの直線が交わるとき
①2直線が平行ならば、同位角(どういかく)は等しい
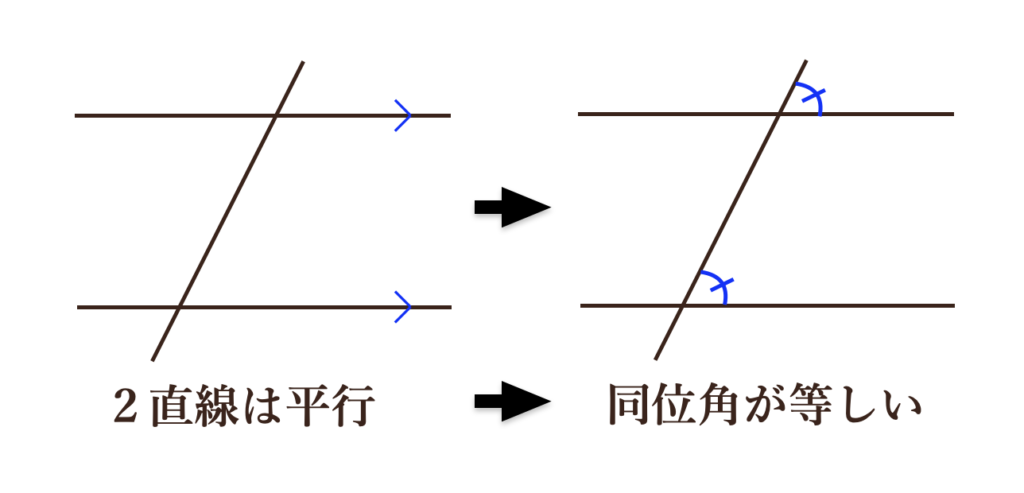
②2直線が平行ならば、錯角(さっかく)は等しい
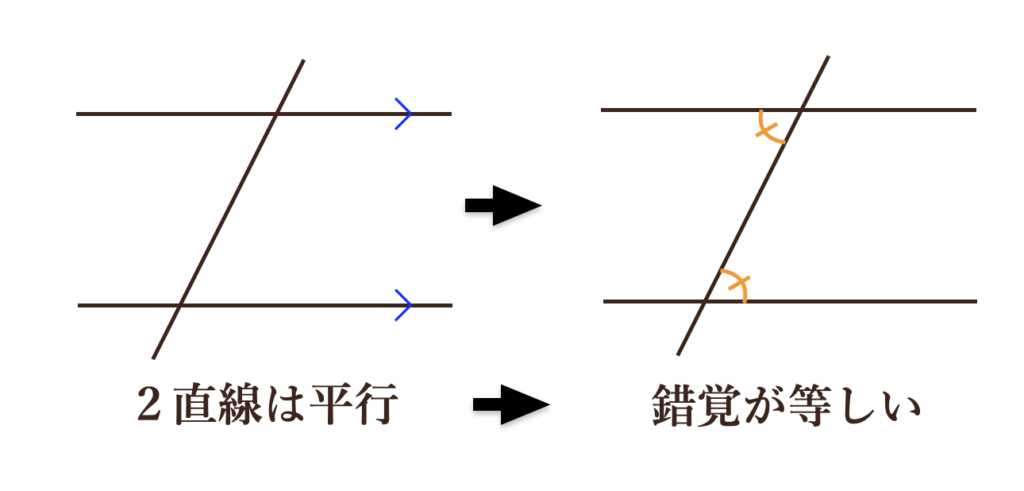
(3)平行線であるための条件
2直線が1つの直線で交わる時
①同位角が等しければ、2直線は平行である
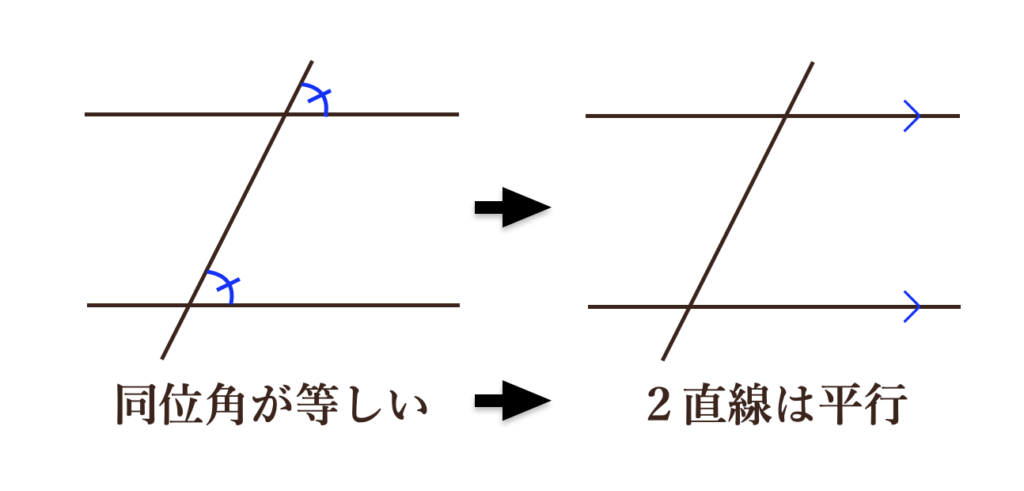
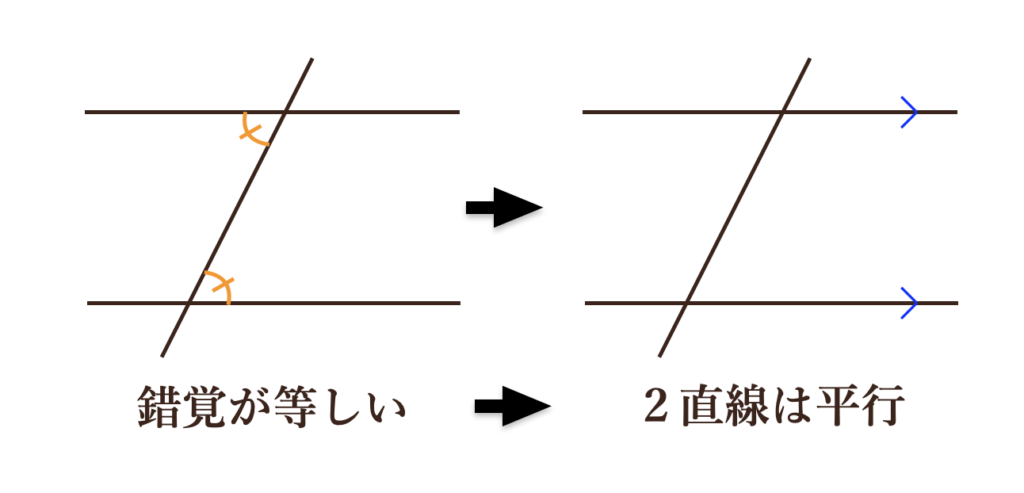
②錯角が等しければ、2直線は平行である
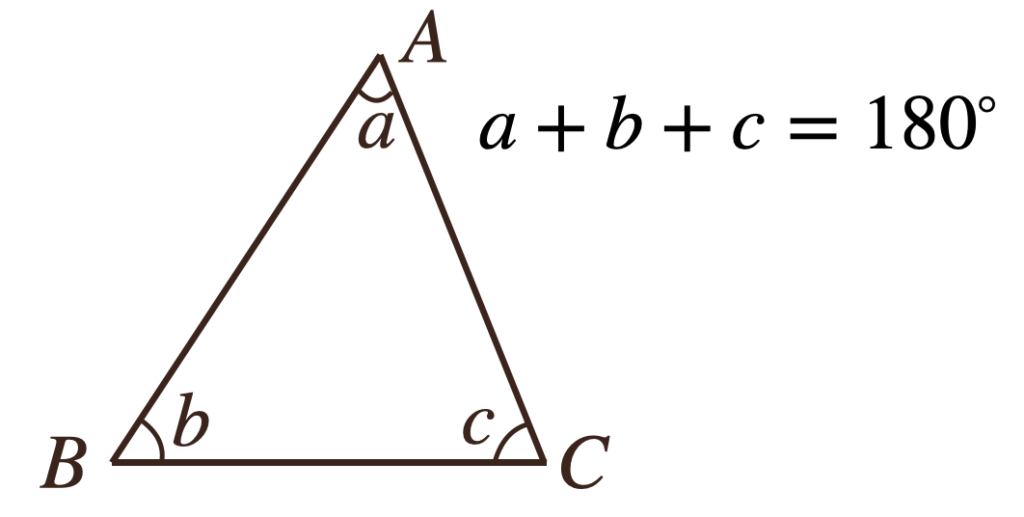
(4)三角形の内角と外角の性質
①三角形の内角の和は180°である
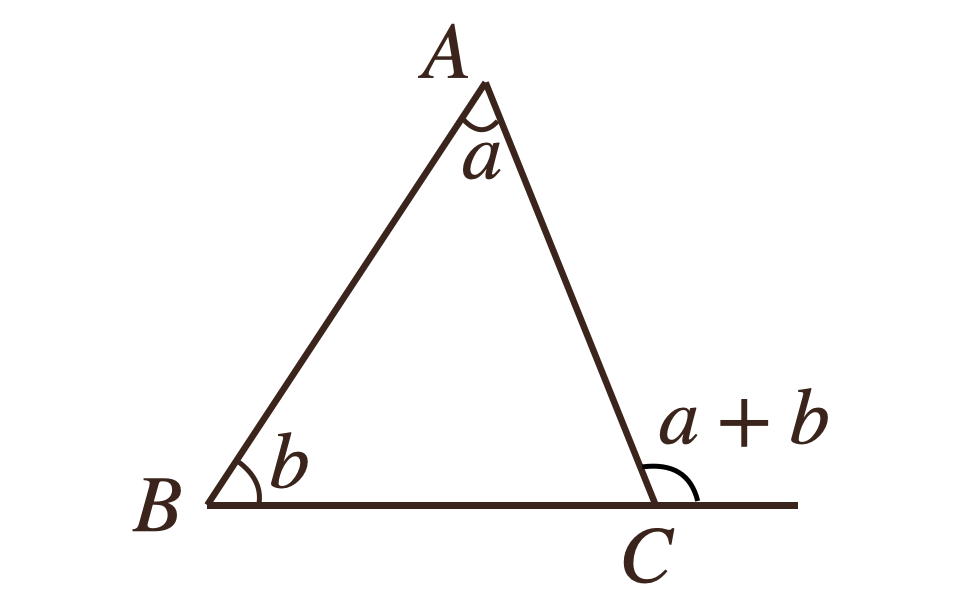
②三角形の1つの外角は、そこと隣り合わない2つの内角の和に等しい
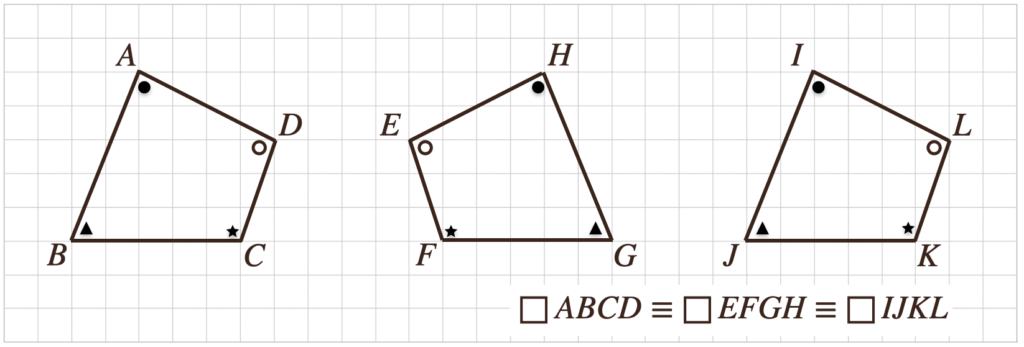
(5)合同な図形の性質
①対応する線分の長さがそれぞれ等しい
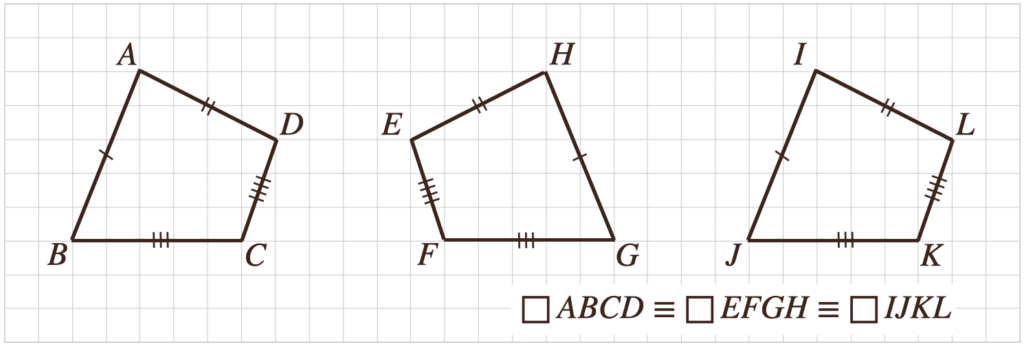
②対応する角の大きさがそれぞれ等しい
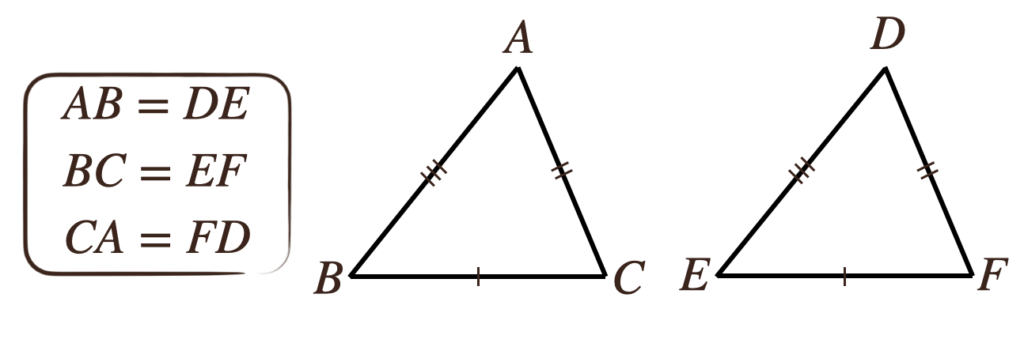
(6)三角形の合同条件
①3つの辺がそれぞれ等しい
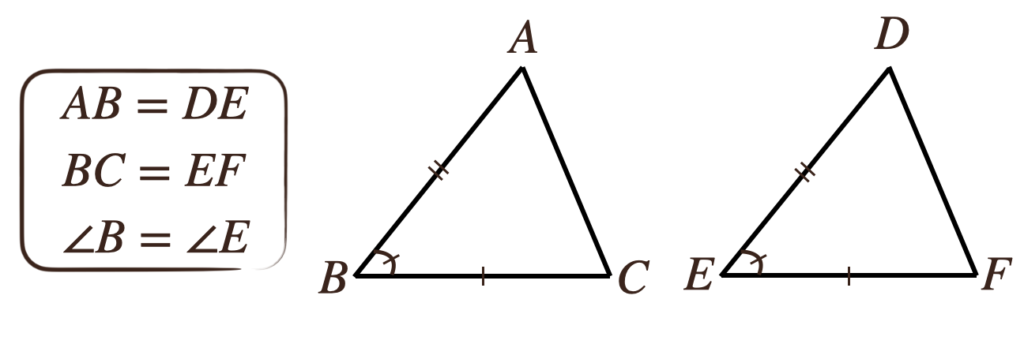
②2つの辺とその間の角がそれぞれ等しい
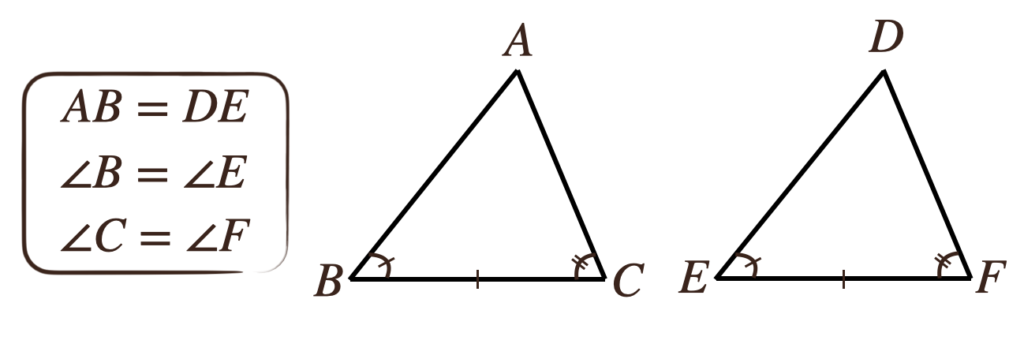
③1つの辺とその両端の角がそれぞれ等しい
ここまでが、中学2年生の「平行と合同」で習った、図形の性質になるね。
これ以外でも証明の根拠となる図形の性質っていうのあるんだけど
ここで挙げていくには、数が多いので、今回はここまでとなります。
ここまでの記事が良かったと思ったらここをクリックしてね。
質問なんかがあった場合はコメントにお願いします。
では、またさようなら



コメント