どうも、こんにちはDKです。
中学2年生で習う、平行と合同の続きやっていきますね。
今回は、平行と合同の「証明」についてやっていきますね。
一つ前のところで、証明のとっかかりの部分を解説したんですけど
この証明っていうのは、なんかむずかしそうって思ってしまう人もいるかと
思うんだけど、証明のやり方っていうのを理解して覚えてしまえば
定型文に言葉を当てはめていくことで、証明することができるものなので
苦手って人は、ここで、基礎をもう一度見直していってください。
動画でも、基礎の解説を行なっているので
そちらをみてみたいって人はこちら↓↓↓ (音が出るので注意して)
ここの「証明」に必要不可欠なものとして
いろいろな性質(三角形の性質、平行線の性質)ってのがあって、これらの性質を
理解していないと、「証明」することができなくなっちゃうので
【 証明の根拠 】←ここから、いろいろな性質のまとめを紹介しているので
見直しを行いたいとときはそっちを見てみてください。
(1)仮定と結論
ここに、\(\angle AOB\)の二等分線を作図したとき
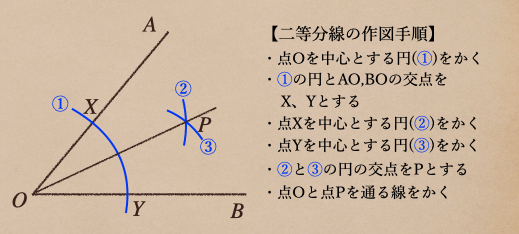
\(OP\)が\(\angle AOB\)の二等分線であることを証明してみよう。
上の図のように作図すれば、OPは\(\angle AOB\)の二等分線っていうことは
明らかなんだけど、ここでの証明っていうのは、言葉で説明をしてあげるってことになるんだね。
まずは、わかっていることをはっきりさせていこう。
点\(X\)と点\(Y\)っていうのは、円(①)の交点ってことなので
同じ円周上にある点ってことになるよね。なので、\(XO=YO\)となるね。
そして、点Pっていうのも、\(X\)と\(Y\)から同じ半径の円(②)、(③)の交点ってことになるので
\(XP=YP\)ってことも言えるよね。
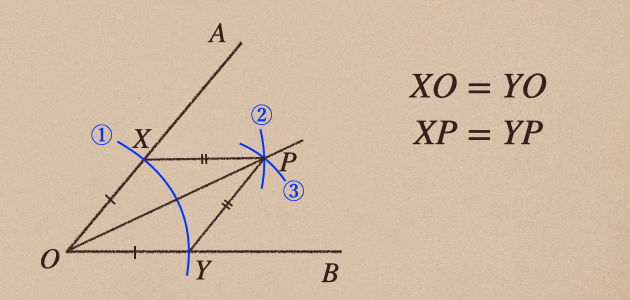
ここで、\(\bigtriangleup XOP\)と\(\bigtriangleup YOP\)で見たとき、\(OP\)っていうのは
共通の辺ってことなので、\(OP=OP\)ってことが言えて
「3つの辺がそれぞれ等しい」ことから、\(\bigtriangleup XOP \equiv \bigtriangleup YOP\)となって、
合同な三角形から\(\angle AOP=\angle BOP\)ってことが言えて
\(OP\)は\(\angle AOB\)の二等分線ってことが証明できたね。
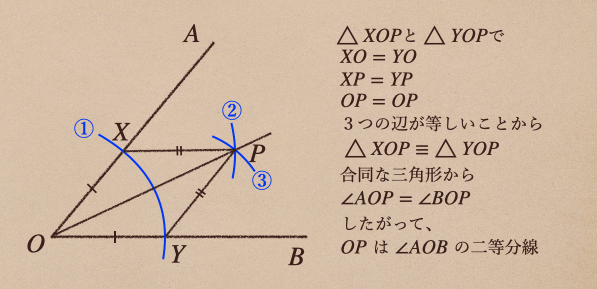
証明を行う際には、上の図のように簡単に伝えたいことだけを書くようにしよう。
ここで、この証明した内容を見て、その考え方っていうのを確認してみよう。
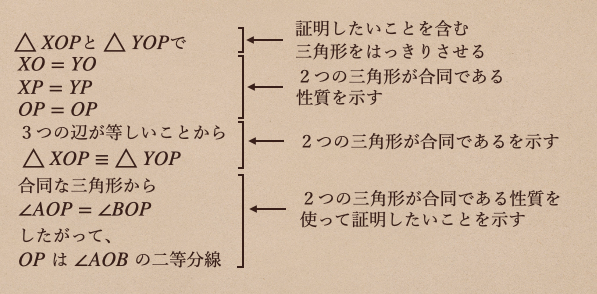
こんな風に、(1)証明したいことを言う、(2)証明したいことの性質を言う、(3)証明する
(4)証明された結果から、真に証明したいことを言う
この、4つの流れで説明していくことで、証明することができるんだね。
ここでの、ポイントとしては、あらかじめ真に証明したいことを言うためには
何が言えれば真の証明を行えるかって言うのを考えてあげるってことなんだね。
今回の場合だと、\(\bigtriangleup XOP \equiv \bigtriangleup YOP\)っていうのが
言えれば、真に証明したい\(OP\)は\(\angle AOB\)の二等分線ってことが言えるってことだね。
今回の証明の中で
「\(XO=YO\)、\(XP=YP\)」ならば「\(\bigtriangleup XOP \equiv \bigtriangleup YOP\)」
であることをはっきりさせたんだけど、この「\(XO=YO\)、\(XP=YP\)」を a 、
「\(\bigtriangleup XOP \equiv \bigtriangleup YOP\)」を b として表したとき
「a ならば b」ってことになるんだけど
このとき a を『仮定(かてい)』、b を『結論(けつろん)』っていう言い方をするんだね。
【仮定と結論】
「a ならば b」
a を『仮定(かてい)』、b を『結論(けつろん)』
{例}「\(\bigtriangleup ABC \equiv \bigtriangleup DEF\)」ならば「\(\angle A =\angle D\)」
「\(\bigtriangleup ABC \equiv \bigtriangleup DEF\)」:仮定 「\(\angle A =\angle D\)」:結論
証明する時っていうのは、結論が成り立つために、仮定から順を追って説明していく必要があって
初めに証明することがらの仮定と結論をはっきりさせておく必要があるんだね。
(2)証明のしくみ
ここでも、下の図を見てみて。
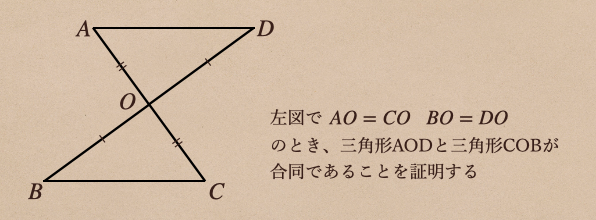
2つの三角形が合同であることの証明だね。
ちなみに、この証明の仮定は「\(AO=CO\)、\(BO=DO\)」で
結論は「\(\bigtriangleup AOD \equiv \bigtriangleup COB\)」ってことだね。
証明はこんな風になるね。
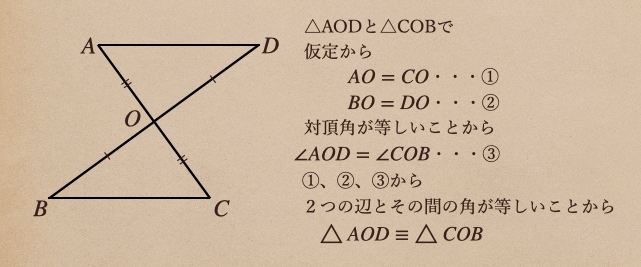
今回の証明のしくみにして見てみると
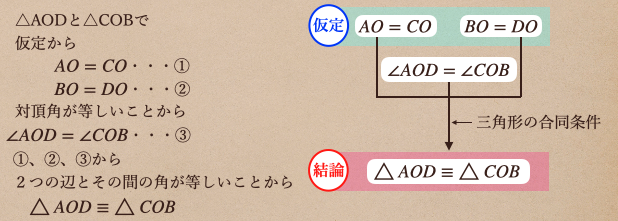
こんな風に図にして、証明の流れっていうのをみてみると証明を少しは理解できたかな?
実際に証明を解く時っていうのは、仮定と結論っていうのをはっきりさせて
この図を思い出しながら証明をしていってもらえると必要となる
求めるべき条件っていうのがわかりやすくなるかなと思うので活用してみてね。
証明の根拠となる、いろいろな性質を、こっちのブログでまとめているので
一度、確認しておこう。 →【 証明の根拠 】
今回は、ここまでになります。
ここまでの記事が良かったと思ったらここをクリックしてね。
質問なんかがあった場合はコメントにお願いします。
では、またさようなら



コメント